 |
Классификация жидких сред. Реологические среды
|
|
|
|
Изучение деформационного поведения и течения реальных жидких сред привело к открытию ряда явлений, не присущих ньютоновским жидкостям. Для них характерно изменение вязкости с изменением скорости сдвига (эффект аномалии вязкости), явление тиксотропии, релаксации, реопекции, высокоэластичные и упругие виды деформации, возникновение нормальных напряжений, существование предельных напряжений сдвига и т.д.
Проявление тех или иных аномальных явлений при приложении
к жидкости внешних сил, прежде всего, зависит от её физической природы, её структуры, а также от внешних факторов.
Необходимо отметить, что ньютоновская жидкость соответствует только узкому специальному случаю. В природе и в промышленности встречаются, в основном, неньютоновские жидкости (реологические среды). Например, продукты фармацевтической, пищевой, лакокрасочной и бумажной промышленности; нефтепродукты и буровые растворы; полимерные материалы, получаемые и перерабатываемые в химической промышленности; высокотемпературные теплоносители на основе полимеров и суспензий; высококонцентрированные наполненные ракетные топлива и топливные смеси в энергетике и т.д.
Реологические среды по своим механическим свойствам занимают промежуточное положение между идеально вязкими (ньютоновскими) жидкостями и идеально упругими гуковкими телами. В материале
под действием внешних сил, в общем случае, развиваются обратимые
и необратимые деформации:
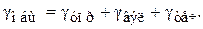 (2.1)
(2.1)
Здесь  – упругая деформация,
– упругая деформация, 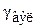 – высокоэластичная деформация,
– высокоэластичная деформация,  – деформация течения. Упругая и высокоэластичная деформации являются обратимыми, течения – необратимая.
– деформация течения. Упругая и высокоэластичная деформации являются обратимыми, течения – необратимая.
Упругая деформация развивается в начальный момент приложения нагрузки, скорость её распространения равна скорости звука в данной среде. После снятия нагрузки она с той же скоростью исчезает. Высокоэластичная деформация развивается во времени, причем скорость этого развития существенно зависит от температуры среды. Величина 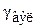 в десятки и сотни раз превышает
в десятки и сотни раз превышает  . Высокоэластическая деформация имеет релаксационный характер. В зависимости от типа и агрегатного состояния материала количественное соотношение между видами деформации может быть разным.
. Высокоэластическая деформация имеет релаксационный характер. В зависимости от типа и агрегатного состояния материала количественное соотношение между видами деформации может быть разным.
|
|
|
В отличие от твердых тел, жидкость не обладает способностью сохранять свою форму, она подвижна и течет под действием силы тяжести.
В гидравлике жидкости рассматриваются как сплошные среды, заполненные массой непрерывно.
Ниже предлагается классификация жидкостей:
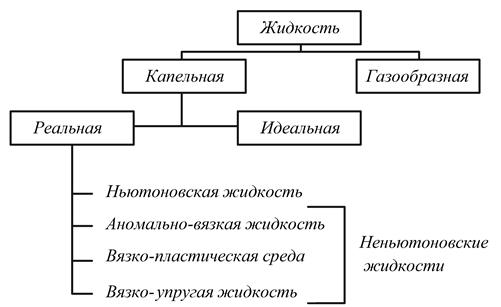
Раздел гидравлики, изучающий деформационное поведение неньютоновских жидкостей, является частью реологии. Реология изучает механическое поведение сред – от ньютоновских жидкостей до твердых тел, подчиняющихся закону Гука.
Газообразные жидкости. Газообразные жидкости под действием силы тяжести занимают весь объем сосуда, не имея поверхности раздела; сжимаемы, при этом сильно нагреваются, маловязкие. Несмотря на это, при малых изменениях давления и температуры (при малых изменениях объема) газы подчиняются тем же законам движения, как и капельные жидкости. Значительные изменения объема при движении газа наступают при скоростях, близких к скорости звука. В отличие от гидравлики, аэродинамика изучает движение газа при небольших скоростях с учетом его сжимаемости, а газодинамика – при скоростях, близких к скорости звука и сверхзвуковых.
Капельные жидкости. Капельные жидкости, почти несжимаемые, под действием силы тяжести занимают объем сосуда, имея поверхность раздела. В определенных условиях, в отличие от газов, на твердой поверхности образуют капли. Капельные жидкости не оказывают сопротивления к растягивающимся нагрузкам, не воспринимают сосредоточенных нагрузок: силы (нагрузки) должны быть рассредоточены по поверхности. В гидравлике изучается поведение капельных жидкостей.
|
|
|
Идеальные жидкости. Идеальные жидкости абсолютно
несжимаемы, молекулы этой жидкости обладают неограниченной свободой движения, следовательно – отсутствуют силы внутреннего трения, т.е. вязкость равна нулю.
Реальные жидкости.
Ньютоновская жидкость. Для случая одномерного течения молекулярный перенос импульса может быть представлен в виде:
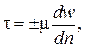 (2.2)
(2.2)
где t – напряжение сдвига, m – коэффициент динамический вязкости жидкости, 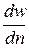 – градиент скорости (скорость сдвига). Зависимость (2.2) является математической формулировкой закона вязкого трения Ньютона: «Касательное напряжение внутреннего трения пропорционально градиенту скорости в направлении
– градиент скорости (скорость сдвига). Зависимость (2.2) является математической формулировкой закона вязкого трения Ньютона: «Касательное напряжение внутреннего трения пропорционально градиенту скорости в направлении 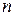 , перпендикулярном движению». Жидкости, подчиняющиеся закону Ньютона, называются ньютоновскими.
, перпендикулярном движению». Жидкости, подчиняющиеся закону Ньютона, называются ньютоновскими.
В зависимости от выбора направления отсчета по нормали градиент скорости может быть положительным и отрицательным. Знак в (2.2) принимается таким, чтобы касательное напряжение было положительным. Для ньютоновских жидкостей вязкость является постоянной величиной,
не зависит от гидродинамической ситуации. Изменение значения вязкости может быть достигнуто изменением температуры жидкости.
Закону Ньютона подчиняются, в основном, низкомолекулярные жидкости.
Аномально-вязкие жидкости. Жидкости, вязкость которых зависит от гидродинамической ситуации, называются аномально-вязкими. Экспериментальные исследования показывают, что зависимость  для многих реальных жидкостей является нелинейной, проявляя изменение вязкости от скорости сдвига и от предыстории жидкости.
для многих реальных жидкостей является нелинейной, проявляя изменение вязкости от скорости сдвига и от предыстории жидкости.
Как установлено, для псевдопластических жидкостей (рис. 2.1
и рис. 2.2, кривая 2) при малых значениях градиента скорости вязкость имеет постоянное значение 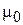 , с увеличением
, с увеличением 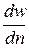 возникает зависимость m от
возникает зависимость m от 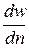 .
.

Рис. 2.1. Кривые течения реальных жидкостей:
1 – ньютоновская; 2 – псевдопластичная; 3 – дилатантная
и 4 – вязко-пластическая среда

Рис. 2.2. Кривые изменения вязкости (обозначения по рис. 2.1)
|
|
|
Значение m с ростом 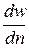 уменьшается до некоторого критического её значения, после чего имеет постоянную величину
уменьшается до некоторого критического её значения, после чего имеет постоянную величину 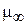 . Следовательно,
. Следовательно,
по 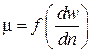 можно установить 3 зоны:
можно установить 3 зоны:
– наибольшей ньютоновской вязкости 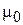 ;
;
– переменной (эффективной) вязкости  ;
;
– наименьшей ньютоновской вязкости 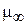 .
.
Установлено, что соотношение 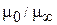 может достичь больших величин –
может достичь больших величин –  .
.
Для описания кривой течения псевдопластичных жидкостей предложены многочисленные зависимости. Наибольшее распространение получила эмпирическая зависимость в виде степенного закона:
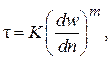 (2.3)
(2.3)
где  и
и  – реологические константы жидкости. Обычно с помощью степенного закона описывают только зону эффективной вязкости.
– реологические константы жидкости. Обычно с помощью степенного закона описывают только зону эффективной вязкости.
Тогда имеем:
 (2.4)
(2.4)
В этом случае 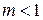 . Несмотря на ограниченность, степенной закон из-за своей простоты нашел широкое применение в инженерной практике. Зависимости, описывающие все зоны кривой течения, дают более сложные уравнения закона сохранения импульса, использование которых вызывает большие математические затруднения.
. Несмотря на ограниченность, степенной закон из-за своей простоты нашел широкое применение в инженерной практике. Зависимости, описывающие все зоны кривой течения, дают более сложные уравнения закона сохранения импульса, использование которых вызывает большие математические затруднения.
Аномалия вязкости для суспензий, содержащих асимметричные частицы, объясняется ориентационными эффектами. Вязкость убывает
до тех пор, пока сохраняется возможность дальнейшего ориентирования частиц. При предельной ориентации частиц вязкость не меняется. Вначале дезориентирующий эффект теплового движения одного порядка
с ориентационными эффектами, поэтому вязкость не меняется. Ориентационными эффектами объясняется аномалия вязкости для расплавов и растворов полимеров, а также эмульсий. Аномалия вязкости для полимеров объясняется также релаксационными процессами.
Для дилатантных жидкостей (рис. 2.1 и рис. 2.2, кривая 3) вязкость повышается с увеличением градиента скорости. Для описания деформационного поведения дилатантных жидкостей может быть использована зависимость (2.3). Но в этом случае  . Дилатантными жидкостями являются концентрированные суспензии и растворы некоторых полимеров.
. Дилатантными жидкостями являются концентрированные суспензии и растворы некоторых полимеров.
Увеличение вязкости связано с увеличением объема (разбухание), занимаемого дисперсной фазой, при этом объем жидких прослоек возрастает. Для новой структуры двухфазной среды жидкости недостаточно для смазки трущихся друг о друга частиц. Этот эффект внешне проявляется как увеличение вязкости суспензии.
|
|
|
Аномально-вязкие жидкости, реологические характеристики которых зависят от времени. Многие реальные жидкости не могут быть описаны уравнениями типа (2.2) и (2.3). Имеются материалы, для которых связь  зависит от времени. Для этих материалов эффективная вязкость зависит не только от градиента скорости, но и от продолжительности сдвига. Эти жидкости в соответствии с тем, возрастает или убывает значение эффективной вязкости во времени (при
зависит от времени. Для этих материалов эффективная вязкость зависит не только от градиента скорости, но и от продолжительности сдвига. Эти жидкости в соответствии с тем, возрастает или убывает значение эффективной вязкости во времени (при 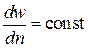 ), делятся на тиксотропные и реопектические.
), делятся на тиксотропные и реопектические.
Тиксотропия связана с разрушением внутренних связей структуры жидкости. Скорость разрушения зависит от числа связей до начала разрушения структуры. С течением времени число связей уменьшается (уменьшается 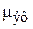 ). В какой-то момент наступает динамическое равновесие
). В какой-то момент наступает динамическое равновесие 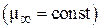 – скорость разрушения и структурообразования будут равны. Тиксотропия является обратимым процессом.
– скорость разрушения и структурообразования будут равны. Тиксотропия является обратимым процессом.
В реопектических жидкостях структурообразование происходит при сдвиге. Например, 42 %-ный водный раствор гипса. После встряхивания этот материал затвердевает в покое за 40 минут, а при медленном встряхивании за 20 секунд.
Следует сказать, что аномалия вязкости, также как и все остальные особенности механического поведения реологических сред, является следствием релаксационного механизма деформации и что все деформационные характеристики среды можно рассчитать, если известна основная релаксационная характеристика среды – её релаксационный спектр.
Вязко-пластическая среда. Вязко-пластическая среда (рис. 2.1, линия 4) характеризуется предельным напряжением сдвига 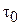 . Вязко-пластическая среда до напряжений
. Вязко-пластическая среда до напряжений 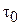 ведет себя как твердое тело.
ведет себя как твердое тело.
С дальнейшим ростом t начинается вязкое (ньютоновское) течение.
Такое поведение жидкостей объясняется тем, что они способны
к образованию пространственных структур; до напряжений 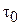 структура сохраняется, в дальнейшем она разрушается. После снятия нагрузки
структура сохраняется, в дальнейшем она разрушается. После снятия нагрузки
в статическом положении пространственная структура среды восстанавливается. Реологическое уравнение вязко-пластическоей среды имеет вид:
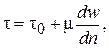 (2.5)
(2.5)
где m – коэффициент пластической вязкости.
Сравнивая зависимости (2.2) и (2.5), введем понятие кажущейся вязкости  :
:

 (2.6)
(2.6)
По характеру течения к вязко-пластическим жидкостям относятся буровые глинистые растворы, шламы, масляные краски, консистентные смазки, пасты и т.д.
Встречаются случаи, когда процесс течения характеризуется
с аномалией вязкости (рис. 2.1, позиция, обозначенная пунктирной линией). Для таких сред реологическое уравнение имеет вид:
|
|
|
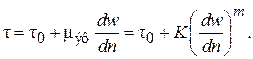 (2.7)
(2.7)
В вязко-пластических средах реализуется два вида деформации – упругая и вязкого течения.
Вязко-упругая жидкость. Вязко-упругая жидкость проявляет
как упругое восстановление формы, так и вязкое течение. Вязко-упругие от вязких жидкостей отличаются также наличием обратимой деформации, они обладают памятью.
Для вязко-упругих жидкостей характерно в условиях простого сдвига наличие нормальных напряжений, ортогональных к плоскости сдвига. Для полимерных материалов нормальные напряжения могут превосходить напряжение сдвига более чем на один порядок. В области малых градиентов скорости они незначительны, в области эффективной вязкости нормальные напряжения резко возрастают. Для вязко-упругих жидкостей характерны релаксационные свойства.
Рассмотрим связь между деформациями и напряжениями в вязко-упругой жидкости при постянном режиме нагружения (s = const) (рис. 2.3).
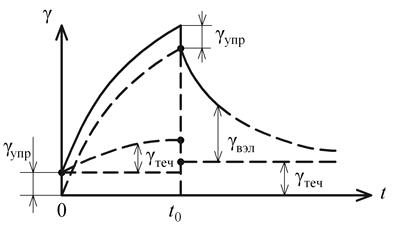
Рис. 2.3. Деформационное поведение вязко-упругой жидкости
при постоянном напряжении нагружения
В начальный момент приложения нагрузки при 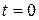 мгновенно реализуется упругая деформация
мгновенно реализуется упругая деформация  , затем до времени
, затем до времени  – высокоэластичная деформация
– высокоэластичная деформация 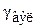 и деформация вязкого течения
и деформация вязкого течения  . При снятии напряжения при
. При снятии напряжения при 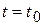 наблюдается мгновенное исчезновение упругой деформации и запаздывающее исчезновение высокоэластичной деформации
наблюдается мгновенное исчезновение упругой деформации и запаздывающее исчезновение высокоэластичной деформации 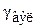 .
.
Реологическое уравнение вязко-упругой жидкости как минимум должно описывать аномалию вязкости и возникновение нормальных напряжений. Оно должно быть достаточно простым для решения прикладных задач и содержать относительно небольшое число материальных констант, определяемых из простых, например, вискозиметрических экспериментов. Всем этим требованиям соответствует уравнение Уайта – Метцнера:
 (2.8)
(2.8)
Здесь s – тензор напряжений, 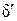 – единичный тензор,
– единичный тензор, 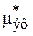 – обобщенная эффективная вязкость,
– обобщенная эффективная вязкость,  – коэффициент нормальных напряжений,
– коэффициент нормальных напряжений, 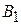 и
и  – кинематические матрицы соответственно скоростей и ускорений деформаций.
– кинематические матрицы соответственно скоростей и ускорений деформаций.
Обобщенная эффективная вязкость может быть определена через интенсивности скорости деформации сдвига Е:
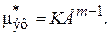 (2.9)
(2.9)
Коэффициент нормальных напряжений  определяется по формуле:
определяется по формуле:
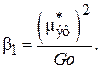 (2.10)
(2.10)
Начальный модуль высокоэластичности  по методу Малкина можно определить, как
по методу Малкина можно определить, как  и
и  , из кривой течения.
, из кривой течения.
В настоящее время известны магнитные жидкости, для которых градиент скорости зависит от напряжения сдвига и приложенного магнитного поля.
В заключение можно сказать, что «каждый материал обладает реологическими свойствами, хотя и в различной степени» (Рейнер – основоположник реологии).
2.2. Поток жидкости. Геометрические элементы
и гидравлические параметры потока
Потоком называется масса движущейся жидкости, ограниченная направляющими твердыми поверхностями. В зависимости от характера
и сочетания твердых поверхностей различают напорные и безнапорные потоки. Гидравлические струи образуются без твердых стенок. Гидравлические струи ограничены жидкостью или газовой средой.
Геометрические элементы потока. Живое сечение S – это поверхность в пределах потока, во всех точках нормальная к направлению вектора скорости (рис. 2.4).

Рис. 2.4. Живое сечение потока
В общем случае площадь живого сечения потока S может быть криволинейной. Однако в инженерных расчетах для упрощения, при небольших углах a, вместо S принимают 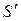 (плоское сечение потока).
(плоское сечение потока).
Смоченный периметр c – часть периметра живого сечения потока,
на котором жидкость соприкасается со стенкой.
Гидравлический радиус  определяется как отношение живого сечения потока к смоченному периметру в этом сечении:
определяется как отношение живого сечения потока к смоченному периметру в этом сечении:
 (2.11)
(2.11)
Эквивалентный диаметр  :
:
 (2.12)
(2.12)
Эквивалентный диаметр является важнейшим линейным параметром живого сечения потока. Например, при определении режима течения потока жидкости критерий Рейнольдса определяется с помощью  .
.
Определим для характерных сечений геометрические элементы потока.
| S | c | R г | 
| |
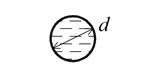 d – внутр. диаметр
d – внутр. диаметр
| 
| p d | 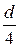
| d |

| ab | 
| 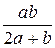
| 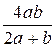
|
 Ширина
пленки b
Ширина
пленки b
| d · b | b | d | 4d |
 D – внутр. диаметр
d – наруж. диаметр
D – внутр. диаметр
d – наруж. диаметр
| 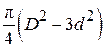
| 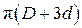
| 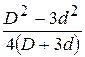
| 
|
Примечание: для кожухотрубного теплообменника определены параметры межтрубного пространства.
Гидравлические параметры потока. Расходом называется количество жидкости, проходящее через живое сечение потока за единицу времени. Различают объемный, массовый и весовой расходы:
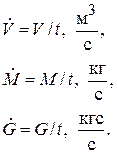 (2.13)
(2.13)
Скорость жидкости в различных точках живого сечения различна
и может меняться во времени  .
.
Средняя скорость потока 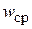 – такая скорость, с которой должны были двигаться все частицы жидкости через S, чтобы расход всего потока был равен расходу, соответствующему действительным скоростям этих частиц:
– такая скорость, с которой должны были двигаться все частицы жидкости через S, чтобы расход всего потока был равен расходу, соответствующему действительным скоростям этих частиц:
 . (2.14)
. (2.14)
В реальных потоках вязкой жидкости местные скорости в различных точках живого сечения будут различными. Зная закон распределения скорости по сечению потока, можно найти объемный расход, следовательно, среднюю скорость потока:
 . (2.15)
. (2.15)
В реальном потоке частицы жидкости кроме основного поступательного движения осуществляют пульсационное беспорядочное движение. Если проекция пульсационной скорости на основное направление течения обозначим через  , то для суммарной скорости можно записать:
, то для суммарной скорости можно записать:
 .
.
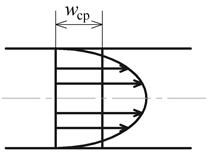
Тогда осредненная по времени скорость (рис. 2.5) данной точки 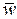 может быть определена по зависимости:
может быть определена по зависимости:
 (2.16)
(2.16)
Необходимо отметить, что время наблюдения (осреднения) 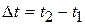 должно быть гораздо больше времени пульсаций.
должно быть гораздо больше времени пульсаций.
Линией тока называется линия, в каждой точке которой в данный момент времени вектор скорости жидкости совпадает направлением касательной к этой точке (рис. 2.6, а). При установившемся движении линия тока и траектория частицы совпадают.
| 
|
Рис. 2.5. Средняя 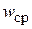 и осредненная и осредненная 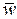 скорости скорости
|

а) б)
Рис. 2.6. Элементы потока: а – линия тока; б – и элементарная струйка
Выделим в жидкости элементарную площадку dS и через все точки на её контуре проведем линии тока (рис. 2.6, б). Полученная поверхность называется трубкой тока. Содержимое трубки тока называется элементарной струйкой. Живым сечением струйки dS называется сечение, нормальное в каждой точке к линии тока.
Свойства элементарной струйки:
– стенки элементарной струйки непроницаемы для частиц жидкости;
– скорости по сечению элементарной струйки одинаковы;
– для установившегося движения форма элементарной струйки
по времени не меняется.
В общем случае скорости w и площади живых сечений dS по длине струйки могут изменяться. Расход (объемный) через живое сечение элементарной струйки можно записать в таком виде:
 (2.17)
(2.17)
Совокупность элементарных струек образует поток жидкости.
|
|
|


