 |
Турбулентное течение жидкости в трубах
|
|
|
|
Хаотичное, неупорядоченное движение жидких частиц существенным образом влияет на характеристики турбулентных течений. Эти течения жидкости – неустановившиеся. Благодаря этому в каждой точке пространства скорости изменяются с течением времени. Мгновенное значение скорости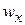 
можно выразить:
(2.42)
где 
– осредненная по времени скорость по направлению x, 
– пульсационная скорость по этому же направлению. Обычно осредненная скорость сохраняет во времени постоянное значение и направление, поэтому такое течение нужно принимать как среднеустановившееся. Когда рассматривается профиль скоростей турбулентного течения для какой-либо области, обычно рассматривают профиль осредненной скорости.
Рассмотрим поведение турбулентного потока жидкости около твердой стенки (рис. 2.17).
Рис. 2.17. Распределение скорости около твердой стенки
В ядре потока за счет пульсационных скоростей происходит непрерывное перемешивание жидкости. У твердых стенок поперечные движения частиц жидкости невозможны.
Около твердой стенки жидкость течет в ламинарном режиме.
Между ламинарным пограничным слоем и ядром потока существует переходная зона.
Движение жидкости при турбулентном режиме всегда сопровождается значительно большей затратой энергии, чем при ламинарном. При ламинарном режиме энергия расходуется на вязкое трение между слоями жидкости; при турбулентном же режиме, помимо этого, значительная часть энергии затрачивается на процесс перемешивания, вызывающий в жидкости дополнительные касательные напряжения.
Для определения напряжения сил трения в турбулентном потоке используется формула:
(2.43)
где 
– напряжение вязкого течения, 
– турбулентное напряжение, вызванное перемешиванием. Как известно, определяется законом вязкого трения Ньютона:
|
|
|
|
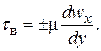(2.44)
Следуя полуэмпирической теории турбулентности Прандтля, принимая, что величина поперечных пульсаций скорости имеет в среднем один и тот же порядок, что и продольные пульсации, можно записать:
. (2.45)
Здесь r – плотность жидкости, l – длина пути перемешивания, 
– градиент осредненной скорости.
Величина l, характеризующая средний путь пробега частиц жидкости в поперечном направлении, обусловлена турбулентными пульсациями.
По гипотезе Прандтля, длина пути перемешивания l пропорциональна расстоянию частицы от стенки:
(2.46)
где c – универсальная постоянная Прандтля.
В турбулентном потоке в трубе толщина гидродинамического пограничного слоя растет значительно быстрее, чем для ламинарного.
Это приводит к уменьшению длины начального участка. В инженерной практике обычно принимают:
(2.47)
Поэтому довольно часто влиянием начального участка
на гидродинамические характеристики потока пренебрегают.
Далее рассмотрим стабилизированный участок горизонтальной круглой трубы.
Рассмотрим распределение осредненной скорости по сечению трубы. Примем касательное напряжение в турбулентном потоке постоянным
и равным напряжению в стенке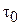 
. Тогда после интегрирования уравнения (2.44) получим:
. (2.48)
Здесь 
– величина, имеющая размерность скорости, поэтому называется динамической скоростью.
Выражение (2.48) представляет собой логарифмический закон распределения осредненных скоростей для ядра турбулентного потока.
Путем несложных преобразований формулу (2.48) можно привести
к следующему безразмерному виду:
(2.49)
где 
– безразмерное расстояние от стенки; M – константа.
Как показывают опыты, c имеет одинаковое значение для всех случаев турбулентного течения 
. Значение M было определено опытами Никурадзе: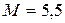 
. Итак, имеем:
|
|
|
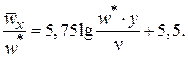(2.50)
В качестве безразмерного параметра, характеризующего толщину соответствующих зон, используется комплекс :
вязкий ламинарный подслой: 
,
переходная зона: 
,
турбулентное ядро: 
.
При турбулентом режиме отношение осредненной скорости
к максимальной осевой составляет от 0,75 до 0,9.
Зная закон распределения скоростей (рис. 2.18), можно найти величину гидравлических сопротивлений. Однако для определения гидравлических сопротивлений можно использовать более простое соотношение, а именно: критериальное уравнение движения вязкой жидкости, полученное ранее, в первой части дисциплины.
Рис. 2.18. Распределение скоростей в трубе
при ламинарном и турбулентном режимах
Для горизонтальной прямой трубы в случае напорного течения вязкой жидкости критериальное уравнение имеет вид:
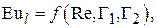(2.51)
где 
– геометрические комплексы, 
– критерий Рейнольдса, 
– критерий Эйлера. Они определяются как:
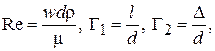
где ∆ – абсолютная шероховатость трубы, l – длина трубопровода,
d – внутренний диаметр трубы. Из опыта известно, что потери давления прямо пропорциональны 
. Поэтому можно записать:
(2.52)
Далее обозначим неизвестную функцию 
, распишем критерий Эйлера 
. Тогда из уравнения (2.52) для потери давления 
получим:
(2.53)
где l – коэффициент гидравлического трения, w – средняя скорость потока.
Полученное уравнение носит название уравнение Дарси – Вейсбаха. Уравнение (2.53) может быть представлено в виде потери напора:
(2.54)
Таким образом, расчет потери давления или напора 
сводится к определению коэффициента гидравлического трения l.
График Никурадзе
Среди многочисленных работ по исследованию зависимости 
выберем работу Никурадзе. Никурадзе подробно исследовал эту зависимость для труб с равномерно-зернистой поверхностью, созданной искусственно (рис. 2.19).
.
Рис. 2.19. График Никурадзе
Значение коэффициента 
определяется по эмпирическим формулам, полученным для различных областей сопротивления по кривым Никурадзе.
1. Для ламинарного режима течения, т.е. при 
, коэффициент l для всех труб независимо от их шероховатости определяется из точного решения задачи о ламинарном течении жидкости в прямой круглой трубе по формуле Пуазейля:
|
|
|
(2.55)
2. В узкой области 
наблюдается скачкообразный рост коэффициента сопротивления. Эта область перехода от ламинарного режима к турбулентному характеризуется неустойчивым характером течения. Здесь наиболее вероятен на практике турбулентный режим
и правильнее всего пользоваться формулами для зоны 3. Можно также применить эмпирическую формулу:
(2.56)
3. В области гидравлически гладких труб при 
толщина ламинарного слоя у стенки d больше абсолютной шероховатости стенок D, влияние выступов шероховатости, омываемых безотрывным потоком, практически не сказывается, и коэффициент сопротивления вычисляется здесь на основе обобщения опытных данных
по эмпирическим соотношениям, например по формуле Блаузиуса:
(2.57)
4. В диапазоне чисел Рейнольдса 
наблюдается переходная область от гидравлически гладких труб к шероховатым. В этой области (частично шероховатых труб), когда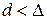 
, т.е. выступы шероховатости с высотой, меньшей средней величины D, продолжают оставаться в пределах ламинарного слоя, а выступы с высотой, большей средней, оказываются в турбулентной области потока, проявляется тормозящее действие шероховатости. Коэффициент l в этом случае подсчитывается также из эмпирических соотношений, например
по формуле Альштуля:
(2.58)
5. При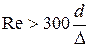 
толщина ламинарного слоя у стенки d достигает своего минимального значения, т.е. 
и не меняется
с дальнейшим ростом числа Re. Поэтому l не зависит от числа Re,
а зависит лишь от e. В этой области (шероховатых труб или области квадратичного сопротивления) для нахождения коэффициента может быть рекомендована, например, формула Шифринсона:
(2.59)
В этой зоне значение l находится в пределах 
.
Были проведены исследования для определения l с естественной шероховатостью. Для этих труб вторая зона не определяется. Для расчета
l обычно предлагаются вышеуказанные формулы.
|
|
|
