 |
Ламинарное движение жидкости в трубах
|
|
|
|
Рассмотрим основные закономерности ламинарного режима
при равномерном движении вязкой жидкости в горизонтальных трубах.
Пусть жидкость входит в круглую трубу из резервуара
большого размера (рис. 2.14). Во входном поперечном сечении скорости
во всех точках будут одинаковы и равны 
. По мере удаления
от входа, вследствие трения у стенок, слои жидкости, прилежащие
к стенкам, начинают затормаживаться; толщина этого слоя d
постепенно увеличивается, а движение, наоборот, замедляется. Центральная часть потока (ядро течения), ещё не захваченная трением, продолжает двигаться как целое. Поскольку расход жидкости – величина постоянная, уменьшение скорости в пограничном слое приведет
к увеличению скорости в ядре потока. Таким образом, в середине трубы,
в ядре, скорость течения всё время возрастает, а у стенок, в растущем пограничном слое d, уменьшается. Это происходит до тех пор,
пока пограничный слой не захватит всего сечения потока,
и ядро не будет сведено к нулю. При этом 
. На этом формирование профиля скоростей заканчивается, в дальнейшем профиль
не меняется и принимает форму, характерную для ламинарного режима
течения жидкости.
Рис. 2.14. Схема развития начального участка в круглой трубе
Участок трубы, на котором происходит стабилизация профиля скоростей, называется начальным участком или участком гидродинамической стабилизации, дальнейший участок – гидродинамически стабилизированным участком. На стабилизированном участке параметры потока не меняются.
Приближенное уравнение пограничного слоя и уравнение неразрывности в цилиндрической системе координат для этого случая имеют вид:
(2.28)
Решение системы уравнений проведено многими авторами,
и результаты представлены в виде:
|
|
|
, (2.29)
где 
Для 
в зависимости от методов решения получены несколько разные результаты: 
– Буссинеск, 
– Тарг, 
– Шиллер, 
– Лыков.
Необходимо отметить, что потери напора на начальном участке больше, чем на соответствующей длине стабилизированного участка.
Это особенно заметно для коротких труб, длина которых меньше начального участка, т.е. 
.
Рассмотрим гидродинамически стабилизированный участок
трубы (рис. 2.15).
Запишем уравнение Навье – Стокса для оси x в цилиндрических координатах r, j, x:
. (2.30)
Рис. 2.15. Течение жидкости в круглой трубе
Заметим, что для горизонтальной трубы 
, течение осесимметричное, т.е. dwx / d j = 0; примем, что инерционные силы по сравнению с остальными незначительны: 
. Тогда из (2.30) получим:
(2.31)
При выводе уравнения Навье – Стокса градиенты давления по осям принимались положительными, а реально давление с ростом x уменьшается. Поэтому можно записать:
Тогда уравнение (2.31) примет вид:
(2.32)
Запишем граничные условия: при 
–конечная величина
Дважды проинтегрировав уравнение (2.32), получим:
(2.33)
Так как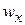 
всюду должна иметь конечное значение, а при 
выражение (2.33) дает 
, то физически реальный результат получим лишь при 
. Для определения 
воспользуемся граничным условием:
Тогда получим:
(2.34)
Таким образом, распределение скоростей по сечению круглой трубы будет параболическим. Максимальное значение скорости получим
при 
, т.е. на оси трубы:
(2.35)
Определим среднее значение скорости 
. Как известно:
(2.36)
Найдем 
. Через элементарное кольцо шириной 
будет проходить количество жидкости, равное (рис. 2.16):
(2.37)
Рис. 2.16. Расход через элементарную площадку
Полный расход через живое сечение трубы будет равен:
(2.38)
Интегрирование (2.38) с учетом (2.34) даст:
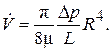(2.39)
Найдем среднее значение скорости , подставляя в (2.36) выражение для расхода :
|
|
|
(2.40)
Сравнивая (2.35) и (2.40), находим, что 
. Из (2.40) определим перепад (потери) давления 
:
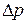(2.41)
Формула (2.41) носит название «формула Пуазейля». Этот закон Пуазейлем был установлен экспериментально.
Полученный закон сопротивления (2.41) показывает, что при ламинарном течении жидкости в трубе круглого сечения потери давления на трение пропорциональны вязкости, длине трубы и средней скорости
в первой степени и обратно пропорциональны диаметру во второй степени.
|
|
|
