 |
Примеры практического использования уравнения Бернулли
|
|
|
|
Поток жидкости состоит из совокупности элементарных струек (рис. 2.10). В различных точках живого сечения потока, имеющего конечные размеры, значения w, p и z различны, т.е. каждая элементарная струйка имеет свое уравнение. Поэтому уравнение Бернулли для потока может быть получено путем суммирования полных энергий всех элементарных струек, составляющих поток.
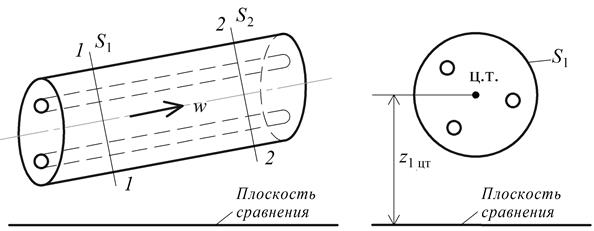
Рис. 2.10. Уравнение Бернулли для потока вязкой жидкости
Определим весовой расход элементарной струйки:
(2.22)
Тогда полная энергия элементарной струйки для данного живого сечения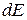 
может быть определена по уравнению:
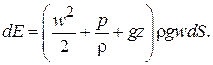(2.23)
Чтобы получить полную энергию потока E в сечении S, нужно сложить энергии отдельных струек. Другими словами, dE нужно проинтегрировать по площади S. Запишем это для двух сечений 1 и 2.
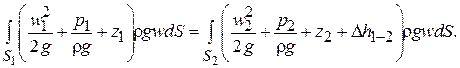(2.24)
В результате получим:
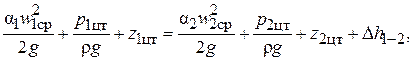(2.25)
где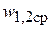 
– средняя скорость потока в сечениях 1–1 и 2–2; 
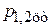– давление в центре тяжести площади живого сечения 
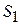и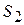 
; 
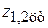– координата центра тяжести 
и ;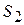 
– средняя потеря напора между сечениями 1–1 и 2–2.
Здесь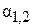 
– коэффициент неравномерности распределения скорости по сечению потока:
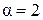– для ламинарного режима;
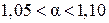– для турбулентного режима.
Коэффициент a называется коэффициентом Кориолиса
и представляет собой отношение действительной кинетической энергии жидкости, протекающей через поперечное сечение потока в единицу времени, и кинетической энергии, которая имела бы место при том же расходе, если бы все частицы жидкости обладали одинаковыми скоростями, равной средней скорости.
В технике обычно встречаются турбулентные потоки, поэтому принимают 
; гидравлика обычно оперирует средними скоростями потоков, поэтому индекс «ср» при скорости w опускают, опускают также индекс «цт» при p и z.
|
|
|
Уравнение Бернулли для потока вязкой жидкости имеет вид:
(2.26)
Как видно, уравнения (2.26) и (2.21) идентичны, однако физический смысл членов уравнений различный.
Приведем примеры использования уравнения Бернулли.
1. Дроссельный расходомер (рис. 2.11).
,
,
.
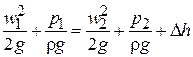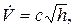
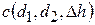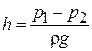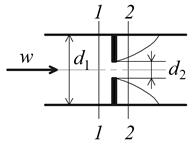
Рис. 2.11. Дроссельный расходомер
2. Эффект Магнуса (рис. 2.12).
,
.
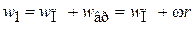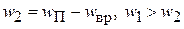Поэтому 
и возникает подъемная сила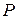 
.
Рис. 2.12. Эффект Магнуса
3. Крученый футбольный мяч (рис. 2.13).
,
.
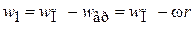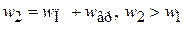Поэтому 
и возникает сила P, направленная вертикально вниз.
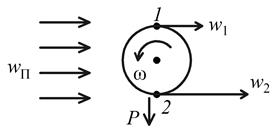
Рис. 2.13. Крученый футбольный мяч
В результате траектория мяча меняется и возникает эффект «сухого листа».
Уравнение Бернулли широко применяется для решения практических задач:
– расчет трубопроводной системы;
– определение высоты всасывания насосов, определение кавитационных явлений;
– определение потребного напора насоса;
– расчет струйных установок;
– определение расхода сужающими устройствами (диафрагма, сопло, труба Вентури, труба Долла и т.д.).
Гидравлическое сопротивление аппаратов и трубопроводов
При движении жидкости в аппаратах и трубопроводах возникают потери энергии, связанные с вязкостью жидкости (ламинарный режим)
и с вихреобразованиями, перемешиванием определенных её объемов (турбулентный режим), а также потери энергии, обусловленные резким изменением конфигурации потока (резкое изменение живого сечения потока и направления потока). Потери первого типа связывают с длиной участка аппарата или трубопровода и называют их гидравлическими потерями по длине и обозначают как 
, второго типа – местными потерями и обозначают как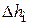 
. Для удобства (упрощения) расчетов считают их независимыми друг от друга и для определения общей потери напора 
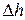их арифметически суммируют:
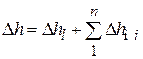. (2.27)
Далее рассмотрим вопросы, связанные с определением и .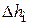
|
|
|
|
|
|
