 |
Нормальный закон распределения
|
|
|
|
В качестве закона распределения случайных ошибок измерения чаще всего принимается нормальный закон распределения (закон Гаусса). Плотность нормального распределения равна 
.
где параметр 
- характеризует точность измерений. Квадрат величины 
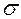называется дисперсией. График плотности распределения вероятностей называется кривой распределения.
На рис. 3.2 показаны кривые плотности нормального распределения при различных значениях 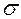. Из этого рисунка видно, что при уменьшении параметра 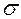кривая нормального распределения сжимается вдоль оси OZ и вытягивается вдоль оси p(z); и, следовательно, чем меньше Z, тем быстрее убывает плотность распределения p(z) с возрастанием Z.
Случайная величина, у которой математическое ожидание равно 0, а дисперсия равна 1, называется стандартной или стандартизованной случайной величиной. При М = 0 и 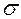= 1 получаем стандартное нормальное распределение N (0,1) укоторогомаксимальная плотность распределения равна p(z) = 1/(2π)0,5 = 0,399 ≈ 0,4 (см. ординату рис. 3.1 и 3.2).
На рис. 3.3 представлены перцентильные ранги из табл. 3.1.
Рис. 3.2. Кривые плотности Рис. 3.3. Накопленные
нормального распределения значения процентов площади
под нормальной кривой
В литературе встречаются разные обозначения математического ожидания: М, а, z, σ.
Z –оценка [ Z = (Х - М) / 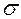] любого значения распределения показывает, на сколько единиц стандартных отклонений данное значение больше или меньше средней арифметической распределения. Z –оценка может быть рассчитана для каждого значения распределения.
Например, рассмотрим распределение коэффициентов IQ. Это распределение является нормальным со средней, равной 100, и стандартным отклонением, примерно равным 15.
|
|
|
Фактически стандартное отклонение распределения коэффициентов IQ равно 16. Однако, чаще используется значение, равное 15, поскольку с ним и коэффициентами, равными 5 или 10, удобнее работать, что реализовано в табл. 3.1.
Таблица 3.1
Значения коэффициентов IQ, их Z –оценки и перцентильные ранги
| Значения коэффициентов IQ | Z - оценка | Процент людей с более низким коэффициентом IQ | Значения коэффициентов IQ | Z - оценка | Процент людей с более низким коэффициентом IQ |
| -3,00 | 0,1 | +0,67 | |||
| -2,67 | 0,4 | +1,00 | |||
| -2,00 | +1,33 | ||||
| -1,33 | +2,00 | ||||
| -1,00 | +2,67 | 99,6 | |||
| -0,67 | +3,0 | 99,9 | |||
| 0,00 |
Характеристики Z –оценок:
1. Например, рассчитаем значение z –оценки, соответствующей коэффициенту IQ, равному 80: Z = (Х - М) / 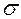= (80 – 100)/15 = - 1,33.
Полученный результат, а также значения, приведенные в табл. 3.1, свидетельствуют о том, что коэффициентам, величина которых меньше средней арифметической, соответствуют отрицательные Z – оценки. И наоборот, коэффициентам, величина которых превышает значение средней, соответствуют положительные Z – оценки.
2. Воспользуемся табл. 3.1 для того, чтобы выразить Z –оценки в терминах, имеющих более содержательный смысл. Так, Z –оценка, равная -0,67, означает, что соответствующее ей значение коэффициента IQ на 0,67 стандартного отклонения меньше средней арифметической.
Коэффициент IQ, равный 130, на два стандартных отклонения больше средней (Z=+2,0). Коэффициент IQ, равный 80 ( расчет которого был только что выполнен), на 1,33 стандартного отклонения меньше средней и т.д.
3. На рис. 3.1 показано, какой процент наблюдений нормального распределения (характеризуемый площадью соответствующего участка графика) размещен между симметрично расположенными положительными и отрицательными Z –оценками. На участке, расположенными между Z –оценками, равными -0,67 и +0,67, заключено 50% площади графика, 68% площади на участке от -1,0 до +1,0; 99,7% площади графика расположено на участке от -3,0 до +3,0.
|
|
|
Z –оценки и связанные с ними значения соответствующих показателей площадей относятся к любому нормальному (и только к нормальному!) распределению.
Вероятность попадания в интервал 
графически изображается площадью соответствующей криволинейной трапеции под кривой распределения вероятностей. В частности, вероятность попадания в симметричный интервал 
изображается площадью фигуры, заштрихованной на рис. 3.1. Отсюда также видно, что чем меньше 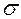, тем меньше разброс ошибок около нуля.
Следует отметить, что площадь под всей кривой плотности распределения равна единице или 100%.
Вероятность попадания нормально распределенной случайной величины: в интервале 
составляет 
,
в интервале 
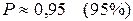и в интервале 
.
Вероятность выхода за трехсигмовые пределы 
настолько мала, что выход случайной ошибки измерения за трехсигмовые пределы считают практически невозможным (правило трех сигм). Другими словами, принимается, что случайные ошибки измерения ограничены по абсолютной величине значением 
( хотя рассматриваемая математическая модель допускает в принципе любые значения ошибок).
Нормальное распределение измеряемой величины полностью определяется величинами а и (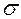
= 3,1415... и е = 2,7182... - математические постоянные). Теоретическое среднее (математическое ожидание) а определяет положение кривой относительно оси 0х. Среднеквадратическое отклонение 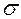определяет форму кривой. Чем больше 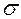(разброс данных), тем кривая становится более пологой (ее основание более широкое).
Когда n велико, то относительные частоты приближенно равны вероятностям 
появления значений 
. Поэтому при большом числе испытаний среднее значение 
мало отличается от 
.
Величина 
называется математическим ожиданием случайной величины x и обозначается как М(x): 
.
Геометрически математическое ожидание представляет собой абсциссу центра тяжести площади под кривой плотности вероятности.
Закон больших чисел: -среднее арифметическое результатов испытаний с ростом n все точнее отражает математическое ожидание испытываемой случайной величины.
|
|
|
Модой (наиболее часто встречающимся значением) случайной величины Х является такое значение М о, в котором плотность вероятности имеет максимальное значение рис. 3.4.
Медианой (срединным значением) случайной величины Х служит значение 
, которое соответствует условию 
. Геометрически медиана представляет абсциссу точек прямой, которая делит площадь, ограниченную кривой плотности вероятности, на две равные части (рис. 3.5).
Рис. 3.4. Определение Рис. 3.5. Определение
моды случайной величины медианы случайной величины
|
|
|
