 |
Проверка гипотезы нормальности распределения
|
|
|
|
1. Метод, основанный на размахе варьирования, позволяет выполнять быструю проверку для широкого класса выборок (от 3 до 1000 измерений). Размах варьирования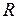 
(разность максимального и минимального значения выборки) делится на среднеквадратическое отклонение 
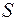и результат сопоставляется с данными табл. 3 Приложения. Если расчетное значение 
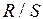расположено между нижней и верхней границами таблицы, то гипотеза нормальности распределения подтверждается. Особенно важно, чтобы это условие соблюдалось при 10% -ном уровне значимости.
Для нашего случая R = 189 – 166 = 23 см; 23/5,5 = 4,182; 4,03 ‹ 4,18 ‹ 5,23;
Гипотеза нормальности распределения по методу размаха варьирования подтверждается.
2. При выборках объемом менее 120 вычисляют среднее абсолютное отклонение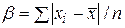 
. Если для нее справедливо выражение 
,
то выборка имеет приближенно нормальный закон распределения.
Для нашего случая 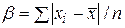= 247/56 = 4,41;
= = | 4,41/5,55 – 0,8 | = 0,0032 ‹ 0,4/√56 = 0,0535;
Гипотеза нормальности распределения по методу среднего абсолютного отклонения подтверждается.
3. Быстрым и простым способом проверки на нормальность является нанесение отклонений на вероятностную сетку. Это графическая бумага, на которой нормально распределенная совокупность отсчетов образует прямую линию.
Вероятностную сетку можно легко изготовить самому с помощью стандартной графической бумаги с линейными шкалами (рис. 4.1 и 4.2). По оси абсцисс равномерно откладываются отклонения, при этом нуль помещается в середину графика. В середине шкалы ординат наносится точка, соответствующая 50%. Вниз от нее откладываются равные интервалы в убывающем порядке: 38,8; 27,6; 19,8; 13,6; 7,9; 4,5; 2,4 и 1,2%. Выше точки 50% откладываются восемь равных отрезков в возрастающем порядке: 61,2; 72,4; 80,2; 87,4; 92,1; 95,5; 97,6 и 98,8%.
|
|
|
На рис. 4.2 показаны линии нормального распределения (А), а также линии распределений, отличающихся от нормального (В – D).
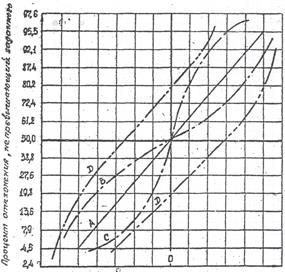
Рис. 4.2. Вероятностная сетка нормального распределения:
А – нормальное распределение; В – симметричное распределение, более плосковершинное, чем нормальное; С - симметричное распределение, более островершинное, чем нормальное; D – асимметричное распределение
Для рассматриваемой выборки n = 56 линия распределения показана в верхней части рис. 4.1, она близка к линии верхней линии D на рис. 4.2 – асимметричное распределение. Полигон распределения в нижней части рис. 4.1 более пологий справа.
4. Некоторое представление о близости эмпирического распределения к нормальному может дать анализ показателей асимметрии и эксцесса, а также стремление нечётных центральных моментов к нулю. Для теоретически нормального распределения значения нечетных моментов равны нулю. М 1 = 0,04/56 = 0,0007; М 3 = 45,14 (46,03) см3;
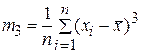- для оценки асимметрии;
А (х) = М 3/ S 3 = 46,03/5,503 = 0,277 › 0;
Если А (х) › 0, то кривая распределения имеет положительную – правостороннюю асимметрию, т.е. правая сторона более пологая (рис. 4.1 внизу), если А (х) ‹ 0, то асимметрия отрицательная – левосторонняя. М 4 = 2356,14 (2356,27) см 4;
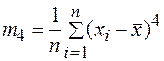- для оценки эксцесса.
Е (х) = М4/S4 – 3 = 2356,27/5,504 – 3 = - 0,427 ‹ 0.
Если Е (х) ‹ 0, то кривая более пологая, чем при нормальном распределении (рис. 4.1 внизу), а при Е (х) › 0 – более островершинная.
Для рассмотренного случая кривая распределения имеет положительную – правостороннюю асимметрию, она более пологая, чем при нормальном распределении.
Пологий характер распределения можно оценить, сопоставляя максимальную плотность нормального распределения 0,4 (рис. 3.2 при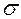 
= 1,0) с максимальным значением относительной частоты табл. 4.2 - D h 3 = h 3 / n = 15/56 = 0,268 ‹ 0,4.
5. Определяем доверительные интервалы математического ожидания при различных уровнях доверительной вероятности: Р = 0,9; 0,95; 0,999
|
|
|
, 
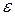= 2,004х 5,50/√55 = 1,49 см;
где 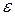- половина доверительного интервала (
);
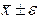t - множитель, определяется по таблице.
Математическое ожидание среднего роста при доверительной вероятности 95 % находится в интервале от 174,17 до 177,15 см.
6. Для глубокой проверки гипотезы нормальности распределения применяются критерии Пирсона (хи-квадрат) и Колмогорова-Смирнова.
Если проверка гипотезы нормального распределения дает отрицательный результат, то необходимо или преобразовать имеющееся распределение к нормальному, например, используя логарифмы, или подобрать другой закон распределения, соответствующий полученным экспериментальным данным: логарифмически-нормальное, Вейбулла, гамма-распределение и др.
Тесты
|
|
|
