Основные законы распределения случайных величин

Коэффициент вариации V – является характеристикой закона распределения случайных величин: V ‹ 0,35 – близок к нормальному закону; V › 0,35 – закон Вейбулла или логарифмически нормальный; V = 1,0 -экспоненциальный закон распределения случайных величин.

Нормальный закон распределения (законГаусса) (рис. 3.1 и др.).Если распредёление случайной величины подчиняется определенному закону и может быть хотя бы приближенно описано кривой у = ае ^{– bх}, то такое распределение называют нормальным. Так как к коэффициентам а и b предъявляется только одно требование, а именно: а, b > 0, то можно говорить о семействе кривых нормального распределения. С увеличением коэффициента «а» кривая «вытягивается» в высоту; при увеличении коэффициента «b» кривая «сплющивается». Наиболеечасто нормальное распределение используют для оценки распределения внешней нагрузки (или напряжения) на детали и агрегаты автомобиля в различных условиях эксплуатации, при определении суммарной наработки восстанавливаемых изделий до капитального ремонта, наработки до отказа невосстанавливаемых изделий.

Логарифмически-нормальный закон распределения (рис. 3.6) описывает распределение случайной величины, логарифм которой распределен по нормальному закону. Применяют, когда значение случайной величины составляет случайную долю ранее наблюдавшегося явления. Это распределение часто используют при расчете долговечности деталей автомобилей, эксплуатируемых в однородных условиях; при исследовании наработки до отказа многих невосстанавливаемых изделий; при исследовании циклических нагрузок, действующих на детали; для описания явлений усталости при циклической нагрузке, если предположить, что усталостное разрушение наступает в результате накопления единичных повреждений, причем число циклов, вызывающих каждое единичное повреждение, зависит от того, сколько повреждений уже накоплено.

Закон распределения Вейбулла (рис. 3.6). Практика исследования нагруженности агрегатов и деталей автомобилей показывает, что наиболее приемлемым законом распределения для описания их прочности и долговечности является закон распределения, предложенный шведским ученым Вейбуллом. Этому закону хорошо следуют распределения предела упругости ряда металлов, характеристики прочности материалов, усталостная долговечность деталей, наработка до отказа многих невосстанавливаемых деталей (например, подшипников качения); наработка до отказа некоторых изделий, у которых отказ наступает вследствие усталостного разрушения. Результаты обработки эксплуатационных наблюдений по грузовым автомобилям показывают, что ресурсы деталей, лимитирующих надежность, в 60-70 % случаев подчиняются распределению Вейбулла.

Рис. 3.6. Кривые логнормального распределения и распределения Вейбулла

Экспоненциальный закон распределения (рис. 3.7) широко применяется в теории надежности, в теории массового обслуживания и других областях. Экспоненциальному закону распределения подчиняется наработка на отказ многих невосстанавливаемых элементов, этот закон часто используется при рассмотрении внезапных отказов в тех случаях, когда явления изнашивания и старения настолько слабо выражены, что ими можно пренебречь. Экспоненциальное распределение применяют также для описания наработки сложных систем, прошедших период приработки, и для описания времени безотказной работы системы с большим числом последовательно соединенных элементов, если каждый из элементов в отдельности не оказывает большого влияния на отказ системы. Математическое ожидание и среднее квадратическое отклонение такого распределения равны между собой, что является существенным при проверке соответствия экспоненциального распределения теоретическому распределению. Экспоненциальное распределение является частным случаем распределения Вейбулла и гамма - распределения.

Гамма-распределение (рис. 3.7) служит для описания: износовых отказов, отказов вследствие накопления повреждений, наработки системы с резервными элементами, распределения времени восстановления. При различных параметрах гамма-распределение принимает самые разнообразные формы, что и объясняет его широкое применение. Если параметр формы a = 0, то гамма-распределение совпадает с экспоненциальным распределением, при a > 10 – практически совпадает с нормальным распределением. Если a -произвольное целое число, то гамма-распределение называют распределением Эрланга. Если параметр масштаба b = 0,5; а значение параметра формы кратно 0,5; то гамма-распределение совпадает с распределением ХИ - квадрат, которое применяется для проверки согласия эмпирических данных с гипотетической функцией распределения.

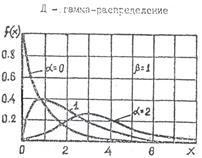
Рис. 3.7. Кривые экспоненциального и гамма-распределений

При обработке экспериментальных данных нередко исследуемую выборку представляют как смесь (суперпозицию)нескольких распределений. По внешнему виду распределения, например, наличию двух или более максимумов, можно судить о целесообразности использования суперпозиции распределения. К таким распределениям могут привести различные причины изготовления и эксплуатации – изготовление одних и тех же деталей на различном оборудовании или по различной технологии, изменение конструкции детали или кузова, различия в условиях эксплуатации.