 |
Порядок действий при заполнении таблицы.
|
|
|
|
Выборку из табл. 4.1 последовательно просматриваем от первой до последней строчки, и при чтении каждого результата соответствующую метку (точку или черточку) заносят в тот класс табл. 4.2, к которому относится данное наблюдение. Каждый знак из четырех точек и шести черточек соответствует десяти наблюдениям, поэтому подсчет частот значительно облегчается.
При заполнении табл. 4.2 надо быть очень внимательным, особенно при заполнении крайних значений каждой строки.
Например, в 1-й строке значение Х=169 исключается, оно входит в следующий 2-й класс: от 169 до 173, причем Х=173 переходит в следующий 3-й класс и т.д.
В 1-й класс из табл. 4.1 войдут: 1. Х 11 = 168; 2. Х 16 = 167; 3. Х 33 = 167; 4. Х 34 = 166; 5. Х 46 = 166. В 4-м столбце «Подсчет частот» эти значения отмечены четырьмя точками и одной горизонтальной линией. В 5-м столбце отмечена абсолютная частота 1-го класса h 1=5. Аналогично во 2-м классе получим h 2=13; в 3-м h 3=15; h 4=14; h 5=5; h 6=4.
å h i = 5+13+15+14+5+4 = n = 56.
В конкретной лабораторной работе № 13 исключено значение Х11 = 168. Остаются h1= 4, это будут: Х4 = 167; Х21 = 167; Х22 = 166; Х34 = 166.
Для лабораторных работ результаты расчетов абсолютных частот каждого класса не должны превышать цифры в 5-м столбце табл. 4.2.
Рассчитываем относительные частоты (частости) D h i = h i / n и накопленные относительные частоты, заполняем табл.4.2.
D h 1 = h 1 / n = 5/56= 0,089; записываем это значение в 6-й и 7-й столбцы.
D h 2 = h 2 / n = 13/56 = 0,232. Записываем это значение в 6-й столбец. Складываем два значения: D h 1+D h 2 = 0,089 + 0,232 = 0,321. Записываем это значение во 2-ю строку 7-го столбца(относительные накопленные частоты).
D h 3 = h 3 / n = 15/56 = 0,268. Складываем это значение с предыдущим значением 7-го столбца. 0,268+0,321 = 0,589. Записываем результат в следующую строку 7-го столбца и т.д.
|
|
|
D h 4 = 14/56 = 0,250. 0,250+0,589 = 0,839. D h 5 = 5/56 = 0,089. 0,089+0,839 = 0,928.
D h 6 = 4/56 = 0,072. 0,072+0,928 = 1,00.
3. Для построения гистограммы по горизонтали отмечаем значения 2-го столбца табл. 4.2: Х = 165, 167, 169 и т.д. до 189. Отмечены границы (165, 169 и т.д.) и середины классов (3-й столбец) 167, 171 и т.д.
По вертикали наносим шкалу абсолютных частот: 5,10,15,20.
Строим столбиковую диаграмму: столбик высотой h 1=5 над Х = 165 - 169; далее столбик h 2 = 13 над Х = 169-173 и т.д. Получили гистограмму выборки.
Соединяем середины вершин столбиков: 5, 13, 15, 14, 5 и 4 ломаной линией - получили полигон частот.
Гистограмма, полигон распределений и кумулятивная линия, построенные по данным табл. 4.2, изображены на рис. 4.1.
Рис. 4.1. Графическое изображение распределения частот:
1-кумулятивная линия, 2-гистограмма, 3-полигон частот;
вверху – вероятностная сетка нормального распределения
Гистограмма и полигон распределений являются графическим отображением частот, которые, в свою очередь, представляют собой оценки плотностей вероятностей.
Над гистограммой и полигоном достраиваем другой график. По оси ординат откладываем значения накопленных относительных частот: 0,1; 0,2: 0,3 и т.д. до 1,0. На этом графике по данным 2-го и 7-го столбцов отмечаем точки: 165 - 0,00; 169 - 0,089; 173 - 0,321; 177 - 0,589; 181 - 0,839; 185 - 0,928 и 189 - 1,00. Соединяем точки ломаной линией – получили кумулятивную линию
Кумулятивная линия – график накопленных частот, в свою очередь оценивающих функцию распределения F(х) в точке х. Очень многие наблюдения в природе при такой обработке дают колоколообразные полигоны распределения.
Над графиком кумулятивной линии строим вероятностную сетку и отмечаем на ней ранее полученные точки в процентах.
Например, вторая точка 0,089 = 8,9%; следующая точка 0,321 = 32,1% и т.д.
4. Выполняем расчеты:
среднее арифметическое (выборочное среднее, первый начальный момент)
= 175,66 см;
упрощенный вариант расчета по данным 3-го и 5-го столбцов табл. 4.2 дает практически такой же результат.
|
|
|
= [(167х5)+(171х13)+(175х15)+(179х14)+(183х5)+(187х4)]/56 = 175,93 см.
эмпирическая дисперсия (второй центральный момент)
= 1695,90/56 = 30,28;
несмещенная дисперсия 
= 1695,90/55 = 30,83;
выборочные среднеквадратичеые отклонения, стандарты
; S = √30,28 = 5,50; ¯ S= √30,83= 5,55;
третий центральный момент 
=2577,70/56= 46,03;
четвертый центральный момент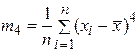 
=131951,25/56= 2356,27;
коэффициент вариации (изменчивости) 
= 5,55/175,66 = 3,16 %;
Точечные и интервальные оценки необходимы для определения истинного значения измеряемого параметра с заданной надежностью.
Сумма в столбце № 3 теоретически должна быть равна нулю (центральный момент первого порядка), и это может служить промежуточной проверкой правильности вычислений. Однако при вычислении с точностью до двух знаков всегда имеет место небольшая неточность, несмотря на соблюдение известного правила вычислений (чередование округлений с избытком и недостатком).
Средний рост группы, состоящей из 56 студентов, оказался равным 175,66 см.
Специалисты по демографии утверждают, что если бы подобное наблюдение было произведено 100 лет назад, то, вероятно, эта величина не достигла бы и 170 см. Тенденция увеличения среднего роста людей в европейских странах общеизвестна. Вспомним хотя бы о рыцарских доспехах, которые в настоящее время пришлись бы в пору только детям.
Отсев грубых погрешностей
Грубые погрешности измерения (аномальные, или сильно выделяющиеся, значения - промахи) очень плохо поддаются определению, хотя каждому экспериментатору ясно, что это такое.
Известно несколько методов определения грубых ошибок статистического ряда.
1. Наиболее простым способом исключения из ряда наиболее выделяющегося измерения является правило трех сигм – разброс случайных величин от среднего значения не должен превышать доверительного интервала величиной в три среднеквадратических отклонения (стандарта).
.
Для нашего случая 175,66 +- 3х 5,55 = 175,66 +- 16,65; 175,66 – 16,65 = 159,01;
175,66 + 16,65 = 192,31; 159,01 ‹ 175,66 ‹ 192,31 см; Эти результаты отмечены на рис. 4.1.
По правилу трех сигм грубые ошибки в выборке отсутствуют.
2. Метод максимального относительного отклонения применяют, как правило, для выборки небольшого объема (n ≤ 25). Критерии появления грубых ошибок на основе z = (Х-М)/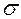 
вычисляют по формуле: τр = |Xi - Xср| / 
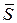≥ τn,р ;
|
|
|
|189-175,66| / 5,55 = 13,34 / 5,55 = 2,40;
Расчетное значение сравнивают с табличным, если неравенство соблюдается, то наблюдение исключают. На практике обычно используют надежность вывода «р = 0,95» - результат получается с 95% доверительной вероятностью. В табл. 1 Приложения, экстраполируя табличные данные к нашей выборке, получим τn,р не менее 2,023 для р = 0,95; а τ n,р не менее 2,417 для р = 0,98.
По методу максимального относительного отклонения грубые ошибки в выборке отсутствуют при надежности вывода 0,98. Измерение 189 см расположено в симметричном интервале рис. 4.1 занимающем 98% площади. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.
3. Более достоверными являются методы, базируемые на использовании статистических критериев.
Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения грубых ошибок (аномальных значений) отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением.
Критическое значение τ р (р – процентная точка нормализованного выборочного отклонения) выражается через критическое значение распределения Стьюдента t (p, n-2):
t (p, n) = (t (p, n-2) √ n -1) / (√ n -2 + [ t (p, n-2) ]2 );
Процедура вычислений отсева грубых погрешностей:
1) Из исходных данных выбираем наибольшее отклонение 189 – 175,66 = 13,34 см;
2) По ранее приведенной формуле определяем расчетное значение критерия максимального относительного отклонения τ р = | Xi - X ср| / 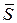=|189-175,66| / 5,55 = 2,40;
3) Находим по табл. 2 Приложения табличные значения процентных точек распределения Стьюдента t (p, n-2) : t (5%,54) = 1,6735; t (0,1%,54) = 3,2574;
4) Вычисляем соответствующие точки:
t (5%, 54) = (t (p, n-2) √ n -1) / (√ n -2 + [ t (p, n-2) ]2 ) = (1,6735 √55) / (√54х1,67352 ) = 1,648;
|
|
|
и (3,2574 √55) / (√54 х 3,25742) = 3,005;
Значение τ р = 2,40 находится между двумя табличными критическими значениями: 1,648 ‹ 2,40 ‹ 3,005. В этом случае отсев выделяющегося наблюдения нужно проводить с большой осторожностью, лучше всего от него воздержаться.
Предположим, что при переписывании таблицы исходных данных вкралась грубая ошибка; например, в строке 13 вместо 189 см записано 289 см.
Тогда τ р = | X i - | / 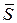= (289 – 175,66)/5,55 = 20,42. Полученное значение относительного отклонения безусловно больше критического табличного значения τ(р, n) при любом значении «р», следовательно, такое наблюдение должно быть отсеяно как грубая погрешность.
Как видно из приведенного примера, рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальное относительное отклонение в процессе вычисления могут быть разделены на три группы: 1) τ ≤ τ (5%, n) ; 2) τ (5%, n) ‹ τ ‹ τ(0,1%, n) ; 3) τ › τ (0,1%, n).
Наблюдения, попавшие в первую группу, нельзя отсеивать в любом случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы отсеивают всегда.
|
|
|
