 |
Тема 2. Линейное программирование
|
|
|
|
Задачами линейного программирования (ЛП) называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств неравенств и для которых методы математического анализа оказываются непригодными. ЛП представляет собой наиболее часто используемый метод оптимизации.
Рассмотрим систему  уравнений и неравенств с
уравнений и неравенств с  переменными (неизвестными):
переменными (неизвестными):
 (1)
(1)
и линейную функцию:
 (2)
(2)
Требуется найти решение системы (1) 

 при котором целевая функция
при котором целевая функция  принимает оптимальное значение (максимальное или минимальное).
принимает оптимальное значение (максимальное или минимальное).
Такая задача называется задачей линейного программирования в общем виде. Система (1) называется системой ограничений (областью допустимых решений). Функция (2) называется целевой функцией.
Оптимальным решением задачи ЛП называется решение  системы ограничений (2), при котором целевая функция принимает оптимальное значение.
системы ограничений (2), при котором целевая функция принимает оптимальное значение.
Рассмотрим задачу ЛП в стандартной форме для случая двух переменных  :
:
 (9)
(9)
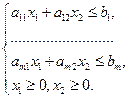 (10)
(10)
Пусть система неравенств (10) совместна (имеет хотя бы одно решение). Любое неравенство этой системы геометрически определяет полуплоскость с граничной прямой 
 Условия не отрицательности определяют полуплоскости с соответственными граничными прямыми
Условия не отрицательности определяют полуплоскости с соответственными граничными прямыми  и
и  .
.
Так как система совместна, то полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность всех этих точек называется многоугольником решений. Это может быть точка, отрезок, луч, прямая, замкнутый многоугольник, неограниченная многоугольная область.
Решение ЗЛП геометрически представляет собой поиск такой точки многоугольника решений, координаты которой доставляют целевой функции наибольшее (наименьшее) значение. Причем допустимым решением являются все точки многогранника.
|
|
|
Рассмотрим так называемую линию уровня целевой функции z, то есть линию, вдоль которой эта функция принимает одно и то же фиксированное значение  :
:  или
или 
Алгоритм решения задачи линейного программирования графическим методом (число переменных  ).
).
1. Строится многоугольная область допустимых решений на плоскости  соответствующая ограничениям. Затем строится вектор-градиент
соответствующая ограничениям. Затем строится вектор-градиент
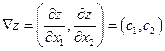
целевой функции z в любой точке  область допустимых решений.
область допустимых решений.
2. Прямая  (линия уровня функции z), перпендикулярная вектору-градиенту, передвигается параллельно самой себе в направлении вектора-градиента в случае задачи на максимум (и в противоположном направлении - в случае задачи на минимум) до тех пор, пока она не покинет область допустимых решений. Предельная точка (или точки) области являются оптимальными точками.
(линия уровня функции z), перпендикулярная вектору-градиенту, передвигается параллельно самой себе в направлении вектора-градиента в случае задачи на максимум (и в противоположном направлении - в случае задачи на минимум) до тех пор, пока она не покинет область допустимых решений. Предельная точка (или точки) области являются оптимальными точками.
3. Для нахождения координат оптимальной точки, надо решить систему уравнений, которая соответствует прямым, пересечение которых образует эту точку. Значение целевой функции в этой точке будет оптимальным, а сами координаты точки будут являться решением задачи ЛП.
Пример. Решить геометрически задачу:

Построим многоугольник всех допустимых решений OABCD и направляющий вектор целевой функции  (Рис. 1). Направление вектора-градиента указывает направление возрастания целевой функции. Так как рассматриваемая задача на отыскание максимума, то прямую, перпендикулярную вектору
(Рис. 1). Направление вектора-градиента указывает направление возрастания целевой функции. Так как рассматриваемая задача на отыскание максимума, то прямую, перпендикулярную вектору  перемещаем в направлении этого вектора параллельно самой себе до тех пор, пока эта прямая не покинет область допустимых решений. На границе области, в нашем случае в точке С, и будет решение задачи. Точка C находится на пересечении прямых
перемещаем в направлении этого вектора параллельно самой себе до тех пор, пока эта прямая не покинет область допустимых решений. На границе области, в нашем случае в точке С, и будет решение задачи. Точка C находится на пересечении прямых  и
и  . Следовательно, ее координаты определяются решением системы этих уравнений уравнении:
. Следовательно, ее координаты определяются решением системы этих уравнений уравнении:
|
|
|

откуда  т.е. точка С имеет координаты (6, 4).
т.е. точка С имеет координаты (6, 4).

Рис. 1
Максимум (максимальное значение целевой функции) равен:  Ответ:
Ответ:  при оптимальном решении
при оптимальном решении  т.е. максимальна прибыль может быть достигнута при производстве 6 единиц первой и 4 единиц второй продукции.
т.е. максимальна прибыль может быть достигнута при производстве 6 единиц первой и 4 единиц второй продукции.
Решить геометрически задачу линейного программирования:

Из рисунка 2 видно, что область допустимых значений неограниченна. Перемещая линию уровня функции z в направлении убывания целевой функции (т.е. в направлении, противоположном вектору  ), убеждаемся, что она всегда будет пересекать область допустимых значений, следовательно целевая функция неограниченно убывает.
), убеждаемся, что она всегда будет пересекать область допустимых значений, следовательно целевая функция неограниченно убывает.
Ответ запишется следующим образом: конечного оптимума целевая функция не имеет, 
Пример. Решить задачу линейного программирования симплекс-методом:

Решение. Приведем систему ограничений к каноническому виду. Получим расширенную систему:

Целевую функцию представим в виде  Базисными переменными будут являться дополнительные переменные
Базисными переменными будут являться дополнительные переменные  .
.
Заполняем первую симплекс-таблицу:
| Базис | Свободный член | Переменные | Оценочные | |||||
| отношения | ||||||||

| 
| 
| 
| 
| 
| |||

| 18/3 | |||||||

| ||||||||

| ||||||||

| 
| |||||||

| -2 | -3 |
Проверяем критерий оптимальности задачи. В последней оценочной строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю - (-3). Следовательно,  . Переменная
. Переменная  является выводимой из базиса а соответствующий ей столбец - разрешающим.
является выводимой из базиса а соответствующий ей столбец - разрешающим.
Находим оценочные отношения и выбираем из них минимальное (5). Следовательно,  , переменная
, переменная  является вводимой в базис, а соответствующая ей строка - разрешающей. Переходим к новой симплекс-таблице:
является вводимой в базис, а соответствующая ей строка - разрешающей. Переходим к новой симплекс-таблице:
а) в новом базисе основные переменные  ;
;
б) расставляем 0 и 1; например, на пересечении столбца и строки, соответствующих переменной  ставим 1, а остальные элементы столбца
ставим 1, а остальные элементы столбца  равны 0 и т.д. Третья строка получается делением на разрешающий элемент
равны 0 и т.д. Третья строка получается делением на разрешающий элемент  . Остальные клетки таблицы заполняем по формулам (2). Например:
. Остальные клетки таблицы заполняем по формулам (2). Например: 

Получаем вторую симплекс-таблицу:
|
|
|
| Базис | Свободный член | Переменные | Оценочные | |||||
| отношения | ||||||||

| 
| 
| 
| 
| 
| |||

| -3 | |||||||

| -1 | 11/2 | ||||||

| 
| |||||||

| ||||||||

| -2 |
Критерий оптимальности вновь не выполнен. Теперь разрешающий первый столбец и  - вводимая переменная. Считаем оценочные отношения и находим разрешающую строку - первая и выводимую из базиса переменную -
- вводимая переменная. Считаем оценочные отношения и находим разрешающую строку - первая и выводимую из базиса переменную -  .Разрешающий элемент
.Разрешающий элемент  .
.
Переходим к новой симплекс-таблице:
| Базис | Свободный член | Переменные | Оценочные | |||||
| отношения | ||||||||

| 
| 
| 
| 
| 
| |||

| -3 | |||||||

| -2 | 5/5 | ||||||

| 5/1 | |||||||

| -3 | 12/9 | ||||||

| -3 |
и на этот раз критерий оптимальности не выполнен.
Выводимая переменная  ; вводимая переменная-
; вводимая переменная-  . Переходим к новой таблице.
. Переходим к новой таблице.
| Базис | Свободный член | Переменные | Оценочные | |||||
| отношения | ||||||||

| 
| 
| 
| 
| 
| |||

| -1/5 | 3/5 | ||||||

| -2/5 | 1/5 | ||||||

| 2/5 | -1/5 | ||||||

| 3/5 | -9/5 | ||||||

| 4/5 | 3/5 |
Критерий оптимальности выполнен. Следовательно,  Оптимальное решение
Оптимальное решение 
Контрольное задание №2.
Решить графически и симплекс-методом задачу линейного программирования:
1. 
| 2. 
| 3. 
|
4. 
| 5. 
| 6. 
|
7. 
| 8. 
| 9. 
|
10. 
|
|
|
|


