Тема 4. Динамическое программирование

Динамическое программирование - это метод оптимизации, приспосо6ленный к операциям, в которых процесс принятия решений может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Динамическое программирование дает возможность принять ряд последовательных решений (многошаговый процесс), обеспечивающих оптимальность развития процесса в целом.

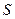Рассмотрим управляемый процесс. Пусть управление можно разбить на шагов, т.е. решения принимаются последовательно на каждом шаге, а управление, переводящее систему из состояния в состояние 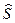представляет собой совокупность пошаговых управлений.

Пусть 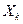- управление на 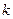- ом шаге и 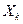удовлетворяет некоторым ограничениям и в этом смысле называется допустимым, где 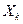- число, точка, функция, качественный признак. 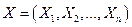- управление, переводящее систему 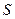из состояния в состояние 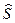. 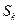- состояние системы после 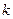- го шага управления. - целевая функция, показатель эффективности рассматриваемой управляемой операции. Целевая функция зависит от начального состояния системы и управления Х.

Предположим:

1. Состояние 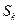зависит только от предыдущего состояния и управления на предыдущем шаге и не зависит от предшествующих состояний и управлений. Это требование называется «отсутствие последствий»: 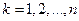- уравнение состояний.

2. Целевая функция 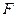является аддитивной от показателей эффективности на каждом шаге. Обозначим показатель эффективности 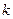- гошаге через: 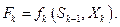Тогда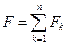

Задача динамического программирования (пошаговой оптимизации) формулируется следующим образом: определить такое допустимое управление Х, переводящее систему 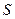из состояния в состояние 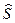при котором целевая функция принимает наибольшее (наименьшее) значение.

Экономические задачи, которые наиболее эффективно решаются на основе динамического программирования, должны удовлетворять следующим условиям.

1. Задача оптимизации интерпретируется как -шаговый процесс управления.

2. Целевая функция равна сумме целевых функций на каждом шаге.

3. Выбор управления на ом шаге зависит от состояния системы к этому шагу, не влияет на предшествующие шаги (отсутствие обратной связи).

4. Состояние системы 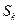после гошага зависит только от предшествующего состояния системы и управления 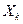(нет последствий).

5. На каждом шаге управление 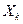зависит от конечного числа управляющих переменных, а состояние 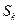от конечного числа параметров.

В соответствии с указанными условиями задача динамического программирования принимает следующий вид:

.

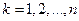Второе функциональное соотношение называется уравнением состояния и обычно оно связывается с ограничениями экономической задачи.

Принципоптимальности Беллмана состоит в следующем: каково бы ни было состояние системы 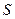в результате какого либо числа шагов, на ближайшем шаге надо выбирать управление так, чтобы оно в совокупности с оптимальными управлениями на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Основное требование принципа оптимальности состоит в том, что процесс управления должен быть без обратных связей, то есть управление на каждом шаге не должно оказывать влияние на предшествующие шаги. При оптимальном управлении, утверждается, что любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого процесс а по отношению к исходному состоянию этого процесса. Следовательно, решение на каждом шаге является наилучшим с точки зрения управления в целом.

Функциональные уравнения Беллмана - это математическая формулировка принципа оптимальности Беллмана. Предположим, что ищется максимум целевой функции.

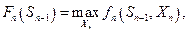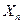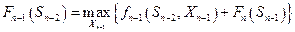На -ом шаге: т.е. выигрыш на - омшаге зависит только от управления на этом шаге. На - ом шаге: , т.е. на - ом шаге надо так подобрать управление ,чтобы сумма выигрышей на - ом шаге 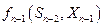и на - ом шаге была максимальна и т.д. На 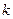- ом шаге

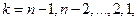, т.е. на 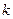- ом шаге надо так подобрать управление 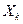, чтобы сумма выигрышей на 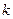- омшаге и на 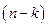последующих шагах 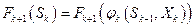была максимальной.