 |
Тема 5. Элементы теории игр
|
|
|
|
На практике часто встречаются ситуации, когда приходится принимать решение в условиях конфликта интересов нескольких участников события. Такие ситуации возникают, например, в карточных играх, шахматах и т.п. В экономике конфликтные ситуации возникают при взаимодействии покупателя и продавца, банка и клиента, поставщика и потребителя и т.д. Особенностью подобных ситуаций является неопределенность, вызванная неизвестным заранее поведением участников конфликта, которые стремятся добиться максимальной реализации своих целей. Математическим описанием конфликтных ситуаций теория игр. Её целью является выработка рекомендаций по разумному поведению участников конфликта.
Основные понятия и общая классификация игр
Всякая математическая модель социально-экономического явления или конфликта должна выражать присущие ему черты, т.е. по крайней мере, отражать следующие его компоненты:
а) заинтересованность сторон;
б) возможные действия каждой из сторон;
в) интересы сторон.
Дадим формальное описание указанных компонент конфликта, вводя при этом принятую терминологию и обозначения.
Заинтересованные стороны будем называть игроками или лицами, а множество всех игроков будем обозначать через 
. Ограничимся рассмотрением случая, когда множество конечно. Не нарушая общности будем считать, что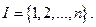 
Любое возможное для игрока 
действие называется его стратегией.
Множество всех стратегий игрока 
обозначим через 
. В условиях конфликта каждый игрок выбирает некоторую свою стратегию 
в результате чего складывается набор стратегий 
называемый ситуацией. Множество всех ситуаций обозначим 
.
Заинтересованность игроков выражается в том, что каждому игроку в той или иной ситуации 
приписывается число, выражающее степень удовлетворения его интересов в этой ситуации. Это число называется выигрышем игрока в ситуации 
и обозначается через 
. Величина называется функцией выигрыша игрока и обычно является действительным числом.
|
|
|
В этих условиях протекание конфликта состоит в выборе каждым игроком его стратегии и в получении им в сложившейся ситуации из некоторого источника выигрыша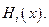 
Таким образом множество игроков, их стратегий и их функций выигрыша полностью описывают некоторую игру 
, что формально записывают так
(1)
Определение Игрой называется действительный или формальный конфликт, в котором имеется, по крайней мере, два игрока, каждый из которых стремится к достижению собственных целей.
Игра как процесс представляет собой многократно повторяющийся выбор игроками своих стратегий, т.е. игру следует считать не как однократный обмен ходами, а как постоянно или, по крайней мере, многократно, осуществляемый процесс.
Определение Игра называется игрой с нулевой суммой, если сумма всех платежей равна нулю, т.е. если сумма проигрышей проигравших игроков равна сумме выигрышей остальных игроков из множества .
Вообще говоря, оценка игроком ситуации путем указания выигрыша 
не всегда возможна практически и даже не всегда имеет смысл. На этом пути создается теория игр с предпочтениями, более широкая, чем теория игр с выигрышами. В дальнейшем будем рассматривать только теорию игр с выигрышами.
Все игры можно разделить на два типа: коалиционные и бескоалиционные. Коалицией называют любое подмножество множества . Игра, в которой действия игроков некоторой коалиции направлены на максимизацию выигрыша всей коалиции без последующего его разделения между игроками коалиции и называются коалиционными. В бескоалиционной игре целью каждого участника является получение по возможности большего индивидуального выигрыша. Существует специальная теория коалиционных игр называемая кооперативной теорией.
|
|
|
Среди всех бескоалиционных игр с нулевой суммой естественным образом выделяется класс антагонистических игр, в которых число игроков равно двум, а значения их функций выигрыша в каждой ситуации равны по величине и противоположны по знаку:
Для сокращения обозначений, множества стратегий игроков 1 и 2 антагонистической игре будем обозначать через и 
, а функция выигрыша 
- через 
Для антагонистических игр с двумя игроками вводится следующее определение.
Определение Пусть каждой стратегии 1-го игрока взаимнооднозначно поставлена в соответствие строка некоторой матрицы 
, а каждой стратегии 2-го игрока взаимнооднозначно поставлен в соответствие столбец этой матрицы. Матрицу называют платежной матрицей (или матрицей игры), если её элемент 
равен выигрышу 1-го игрока (т.е. проигрышу 2-го) при выборе 1-м игроком -й стратегии, а 2-м - 
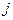-й.
Следовательно, антагонистическая игра полностью описывается единственной платёжной матрицей и в соответствии с этим называется матричной.
Пример. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируются три возможных варианта выпуска данной модели 
. Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль (тыс. р.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей
Выбор в том или ином смысле наилучшего варианта выпуска моделей можно понимать как матричную игру.
|
|
|
