 |
Алгоритм решения задач динамического программирования.
|
|
|
|
Определяем все состояния системы при переходе из начального состояния 
в конечное состояние 
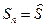. На каждом шаге целевые функции имеют вид: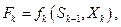 
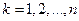и определено уравнение состояния: 
Из уравнения Беллмана для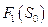 
по находим оптимальное управление на 
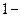ом шаге 
По и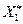 
определяем состояние системы после 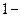го шага: 
Из уравнения Беллмана для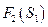 
находим оптимальное управление на 
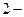ом шаге 
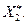По 
и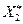 
определяем состояние системы после 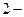го шага: 
и так далее. Условно этот процесс можно представить в виде: 
Задача. Инвестиционная компания планирует вложить средства в четыре проекта. Полная сумма инвестиций составляет 6 млн. рублей. В таблице приведена прогнозируемая доходность проектов для различных объектов инвестиций. Требуется найти наилучший вариант инвестиций, при котором суммарный доход будет максимальным. Предполагается, что прибыльность проектов не зависит от вложений в другие проекты.
| Размер инвестиций | Доходность проектов | |||
| 1-ый проект | 2-ой проект | 3-ий проект | 4-ый проект | |
Решение. Целевой функцией задачи является результирующий доход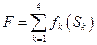 
, при условии 
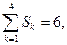где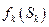 
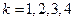- функции дохода 
го проекта при вложении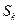 
средств. Зависимость этих функций от объёмов вложений приведены в таблице
Объёмы
вложений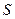 
| 
| 
| 
| 
| ||
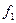
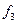
С учётом постановки данную задачу динамического программирования можно разбить на 4 этапа. Каждый этап характеризуется выбором инвестиций в какой то конкретный проект при учёте оптимальных вложений на предыдущих шагах. Математически подобная процедура пошагового выбора имеет вид:
|
|
|
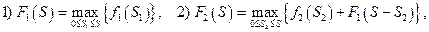
Следовательно, динамическое программирование начинается с первого шага, на котором средства инвестируются в первый проект, и завершается четвёртым шагом, при котором вложения идут в четвёртый проект. Параметр 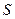в рекуррентных соотношениях меняется от 0 до 6. Функция 
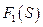, в силу первого из равенств, совпадает с функцией дохода первого проекта и её значения заданы следующей таблицей
|
| |||||||
|
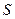
Значения функции 
находим, используя рекуррентное соотношение 2):
1. 
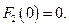
2. 
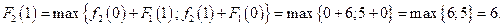
3. 
4. 
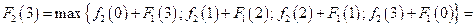
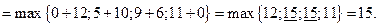
5. 
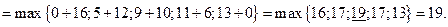
6. 
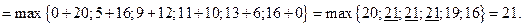
7. 
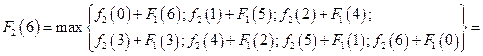
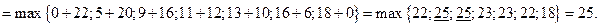
Сведём полученные данные для функции 
в таблицу
|
| |||||||
|
|
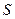
Аналогично, используя рекуррентные соотношения 3) и 4) соответственно, находим значения функций 
. Запишем данные в таблицу
|
| |||||||
| |||||||
|
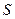
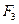
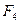
Максимум целевой функции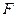 
, равный 28, складывается из расчета:
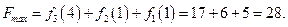
Таким образом, оптимальный план распределения инвестиций имеет вид:
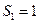млн. руб.; 
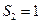млн. руб.; 
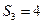млн. руб.
Контрольное задание №4
Предприятие планирует открыть филиалы в Михайловке, Урюпинске и Котельниково, для чего выделяются средства в размере 5 млн. руб.
По расчетам экономистов, каждый филиал при инвестировании в него х тыс. руб. приносит прибыль φi(х) тыс.руб. Эти данные приведены в таблице.
Необходимо выбрать оптимальное распределение выделенных средств между филиалами, обеспечивающее максимальную прибыльность всего проекта.
Вариант 1
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 1,10 | 1,40 | 1,50 | |
| 1,20 | 1,45 | 2,20 | |
| 1,30 | 1,55 | 2,50 | |
| 1,40 | 1,60 | 3,00 | |
| 1,50 | 1,65 | 3,10 |
Вариант 2
|
|
|
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 0,50 | 0,40 | 0,20 | |
| 0,60 | 0,45 | 0,40 | |
| 0,80 | 0,55 | 0,50 | |
| 0,90 | 0,60 | 0,70 | |
| 1,00 | 0,65 | 0,90 |
Вариант 3
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 0,35 | 0,50 | 0,20 | |
| 0,45 | 0,90 | 0,40 | |
| 0,50 | 1,00 | 0,50 | |
| 0,55 | 1,10 | 0,70 | |
| 0,60 | 1,25 | 0,90 |
Вариант 4
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 0,15 | 0,20 | 0,10 | |
| 0,30 | 0,40 | 0,40 | |
| 0,45 | 0,60 | 0,70 | |
| 0,60 | 0,80 | 0,75 | |
| 0,75 | 1,00 | 0,90 |
Вариант 5
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 0,50 | 0,40 | 0,60 | |
| 1,00 | 0,65 | 0,80 | |
| 1,50 | 0,80 | 1,00 | |
| 2,00 | 0,90 | 1,20 | |
| 2,50 | 1,50 | 1,30 |
Вариант 6
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 1,50 | 1,40 | 2,00 | |
| 3,00 | 3,50 | 3,10 | |
| 4,50 | 4,50 | 4,60 | |
| 6,00 | 5,50 | 6,20 | |
| 6,50 | 7,00 | 6,50 |
Вариант 7
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 1,40 | 1,10 | 1,50 | |
| 3,50 | 2,10 | 2,00 | |
| 3,70 | 3,10 | 2,50 | |
| 4,00 | 4,10 | 3,00 | |
| 4,20 | 5,10 | 3,50 |
Вариант 8
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 0,20 | 0,20 | 0,25 | |
| 0,25 | 0,30 | 0,35 | |
| 0,45 | 0,50 | 0,55 | |
| 0,55 | 0,65 | 0,60 | |
| 0,75 | 0,70 | 0,65 |
Вариант 9
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 1,50 | 2,20 | 2,10 | |
| 2,50 | 3,10 | 3,20 | |
| 3,20 | 3,90 | 4,00 | |
| 4,10 | 4,20 | 4,50 | |
| 4,90 | 4,50 | 5,10 |
Вариант 10
| Вложенные средства (x млн.руб.) | Филиал | ||
| Михайловка | Урюпинск | Котельниково | |
| φ1(х) | φ2(х) | φ3(х) | |
| 1,50 | 2,00 | 1,50 | |
| 2,30 | 2,30 | 2,90 | |
| 2,50 | 2,80 | 3,10 | |
| 3,40 | 3,50 | 3,90 | |
| 3,60 | 3,90 | 4,50 |
|
|
|
