Тема 3 Двойственные задачи линейного программирования

Две задачи ЛП, обладающие следующими свойствами называются двойственными.

1. В одной задачи ищется максимум, в другой минимум линейной функции.

2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи.

3. Каждая задача записана в стандартной форме, причем в задаче на минимум все неравенства вида «», а в задаче на максимум - вида «».

4. Матрицы коэффициентов при переменных в системах ограничений

обоих задач являются транспонированными друг к другу: и .

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи.

6. Условия неотрицательности переменных имеются в обеих задачах.

Рассмотрим двойственные задачи ЛП:

Иисходная	Двойственная
Целевая функция:	Целевая функция:
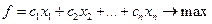
При ограничениях	При ограничениях
и условиях неотрицательности Составить такой план выпуска продукции при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдёт имеющихся запасов.	и условиях неотрицательности Найти такой набор цен оценок) ресурсов при котором общие затраты на ресурсы будут минимальны при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли от реализации этой продукции

Первая (основная) теорема двойственности: если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их целевых функций равны: Если область допустимых решений одной из задач неограниченна, то условия другой задачи противоречивы.

Замечание. Обратное утверждение не верно. Именно: если условия одной задачи противоречивы, это вообще говоря не означает, что другая задача неограниченна.

Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции, выраженной через не основные переменные, ее оптимального решения

Третья теорема двойственности. Компоненты оптимального решения двойственной задачи равны значениям частных производных функции по соответствующим аргументам

Метод, при котором сначала симплекс-методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находится с помощью теорем двойственности, называется двойственным симплекс методом. Он применяется в случаях, когда первое базисное решение недопустимо или при .

Компоненты оптимального решения двойственной задачи называются оптимальными (двойственными или объективно обусловленными) оценками исходной задачи.

Двойственные оценки служат инструментом анализа и принятия правильных решений в условиях постоянно меняющегося производства.

Пример. В результате решения задачи был получен оптимальный план 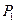и . Появилась возможность выпуска продукции .Затраты каждого ресурса и 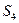на выпуск этой продукции соответственно равны: и 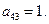Цена продукции Даст ли прибыль включение в план дополнительной продукции?

Решение. Имеем 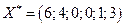и

Сопоставим дополнительные затраты на ресурсы в расчете на единицу продукции с ценой ее реализации:

Полученный результат больше, чем цена продукции Следовательно, ее выпуск не является рентабельным. Очевидно, чтобы включение новой продукции в производство было выгодно, надо, чтобы ее цена мыла не менее 3,6.

Объективно обусловленные оценки ресурсов позволяют судить об эффекте не любых, а лишь сравнительно маленьких изменениях ресурсов. При крупных изменениях меняются сами оценки, что делает невозможным использование оценок для анализа производства.