Последовательность решения задачи

Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса.

Растяжение (сжатие) — такой вид деформации, при котором в любом поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила N, а все остальные силовые факторы равны нулю.

В случае растяжения продольная сила считается положительной, в случае сжатия — отрицательной.

Для определения продольных сил в поперечных сечениях используют метод сечений. Продольная сила в некотором сечении равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.

Чтобы выявить участки бруса или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил на базисной линии, проведенной параллельно оси бруса, для этого:

1. Разбиваем брус на участки, начиная от его свободного конца. Границами участков являются сечения, в которых приложены внешние силы, начало бруса и жёсткая заделка. Например, брус (рис. 24) имеет три участка: АВ, ВС, CD.

2. Используя метод сечений, рассечем брус на участке АВ. Проведём произвольное сечение 1—1 и рассмотрим условия равновесия оставленной правой части (рис. 24, б). Это позволяет определить продольную силу в брусе без определения реактивных силовых факторов в жесткой заделке:

, N₁ – F₁ = 0; N₁ = F₁ = 20 кН.

Рис. 24

Нормальная сила N во всех сечениях по длине участка АВ не изменяется.

3. Проведем сечение 2—2 на втором участке ВС и рассмотрим условие равновесия оставленной правой части бруса (рис. 24, в), получаем:

, N₂ – F₁ – F₂ = 0; N₂ = F₁ + F₁ = 20 + 10 = 30 кН.

4. Запишем условие равновесия правой части бруса, ограниченной сечением 3—3 на участке CD (рис. 4. 5, г):

, N₃ – F₁ – F₂ + F₃ = 0; N₃ = F₁ + F₂ – F₃ = 20 + 10 – 40 = –10 кН.

Знак «–» показывает, что действительное направление силы N₃ противоположно указанному на рис. 24, в. Таким образом, сила N₃ направлена к сечению, и брус на участке CD сжат.

5. Строим эпюру продольных сил (рис. 24, д), откладывая, соблюдая пропорции, и с учётом знаков полученные значения продольных сил в сечениях. Заштрихуем эпюру прямыми линиями, перпендикулярными к базисной линии, параллельной оси бруса. В каждом прямоугольнике в кружке ставим знак продольной силы на данном участке.

6. Определяем нормальные напряжения в характерных сечениях. Чтобы определить нормальные напряжения в брусе при известном значении продольной силы, необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования по­казывают: если нанести на поверхность призматического бруса ряд взаимно перпендикулярных линий, то после приложения внешней рас­тягивающей или сжимающей нагрузки поперечные линии не искрив­ляются и остаются параллельными друг другу. Это соответствует гипотезе плоских сечений (гипотезе Бернулли), согласно которой сечения, плоские до деформации, остаются плоскими и после дефор­мации.

Так как все продольные волокна бруса деформируются одинаково, то и напряжения в поперечных сечениях всех продольных слоев оди­наковы, т. е. σ = const.

откуда                                                

Таким образом, нормальные напряжения, возникающие в попереч­ных сечениях растянутого или сжатого бруса, равны отношению про­дольной силы к площади его поперечного сечения.

7. Строим эпюру нормальных напряжений. Построение эпюры нормальных напряжений выполняется аналогично построению эпюры продольных сил.

8. Определяем полную величину деформации стержня, используя зависимость

,

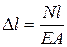где Δ l – продольная деформация рассматриваемого участка стержня, мм;

N – величина продольной силы на рассматриваемом участке, Н;

l – длина рассматриваемого участка, мм;

Е – модуль Юнга для материала стержня, МПа;

А – площадь поперечного сечения стержня на рассматриваемом участке, мм².

Полная деформация стержня определяется как сумма деформаций всех его участков: