Основы оценки сложных систем

123

 

 

го, что затрудняет работу эксперта и сказывается на качестве ре­зультатов экспертизы. В этом случае множественные сравнения позволяют уменьшить до разумных пределов объем поступаю­щей к эксперту информации.

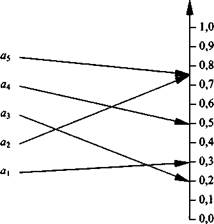
Непосредственная оценка. Метод заключается в присваивании объектам числовых значений в шкале интервалов. Эксперту не­обходимо поставить в соответствие каждому объекту точку на определенном отрезке числовой оси. При этом необходимо, что­бы эквивалентным объектам приписывались одинаковые числа. На рис. 2.6 в качестве примера приведено такое представление для пяти объектов на отрезок числовой оси [0,1].

Поскольку за начало отсчета выбрана нулевая точка, то в дан­ном примере измерение производится в шкале отношений. Экс­перт соединяет каждый объект линией с точкой числовой оси и получает следующие числовые представления объектов (см. рис. 2.6):

Ф (а,) = 0,28; <р (а₂) = <р (а₅) = 0,75; ф (а₃) = 0,2; ф (aj = 0,5.

Оцениваемые объекты

Шкала отношений

Рис. 2.6. Пример сравнения пяти объектов по шкале

Измерения в шкале интервалов могут быть достаточно точ­ными при полной информированности экспертов о свойствах объектов. Эти условия на практике встречаются редко, поэтому для измерения применяют балльную оценку. При этом вместо

непрерывного отрезка числовой оси рассматривают участки, ко­торым приписываются баллы.

Эксперт, приписывая объекту балл, тем самым измеряет его с точностью до определенного отрезка числовой оси. Применя­ются 5-, 10- и 100-балльные шкалы.

Метод Черчмена Акоффа (последовательное сравнение). Этот метод относится к числу наиболее популярных при оценке аль­тернатив. В нем предполагается последовательная корректиров­ка оценок, указанных экспертами. Основные предположения, на которых основан метод, состоят в следующем:

• каждой альтернативе a_t (i = \, N) ставится в соответствие
действительное неотрицательное число ф (а_г);

• если альтернатива a_i предпочтительнее альтернативы а,,
то ф (а,.) > ф (а.), если же альтернативы я_г и я равноценны,
тоф(о₍.) = ф(а_/);

• если ф (я,.) и ф (а.) оценки альтернатив а/ и а •, то ф (а₍.) + ф (а)
соответствует совместному осуществлению альтернатив а/ и а..
Наиболее сильным является последнее предположение об адди­
тивности оценок альтернатив.

Согласно методу Черчмена-Акоффа альтернативы a_t, a ₂,..., a_N ранжируются по предпочтительности. Пусть для удобства из­ложения альтернатива a_l наиболее предпочтительна, за ней сле­дует а₂ и т.д. Эксперт указывает предварительные численные оцен­ки ф (flj) для каждой из альтернатив. Иногда наиболее предпоч­тительной альтернативе приписывается оценка 1, остальные оценки располагаются между 0 и 1 в соответствии с их предпоч­тительностью. Затем эксперт производит сравнение альтернати­вы a_l и суммы альтернатив а₂, ••• > ^ан- Если а\ предпочтительнее, то эксперт корректирует оценки так, чтобы

N

В противном случае должно выполняться неравенство

Если альтернатива а_; оказывается менее предпочтительной, то для уточнения оценок она сравнивается по предпочтению с суммой альтернатив а₂,а₃,..., a_N _, и т.д. После того как альтер-

124

Глава 2

 

 

\ pat ;, (1-р)а/] предпочтительнее, чем \р'а{, (1-р') в/], если/»/?' и др. Если указанная система предпочтений выполнена, то для каж­дой из набора основных альтернатив al, а2,..., aN определяют­ся числа jf], х2,..., xn, характеризующие численную оценку сме­шанных альтернатив. Численная оценка смешанной альтернативы \ pl alt р2а2,..., PN aN ] равна х, />, + х2р2 +... + xNpN. Смешанная альтернатива \р^а^ р2а2,..., pNaN ] предпочтитель­нее смешанной альтернативы \р\ а,, р "2 аг,..., p ' N aN ], если

натива a_l оказывается предпочтительнее суммы альтернатив а₂,..., a_k (к > 2), она исключается из рассмотрения, а вместо оцен­ки альтернативы а, рассматривается и корректируется оценка аль­тернативы я₂- Процесс продолжается до тех пор, пока откоррек­тированными не окажутся оценки всех альтернатив.

При достаточно большом N применение метода Черчмена-Акоффа становится слишком трудоемким. В этом случае целесо­образно разбить альтернативы на группы, а одну из альтерна­тив, например максимальную, включить во все группы. Это по­зволяет получить численные оценки всех альтернатив с помощью оценивания внутри каждой группы.

Метод Черчмена-Акоффа является одним самых эффектив­ных. Его можно успешно использовать при измерениях в шкале отношений. В этом случае определяется наиболее предпочтитель­ная альтернатива я₍₁. Ей присваивается максимальная оценка. Для всех остальных альтернатив эксперт указывает, во сколько раз они менее предпочтительны, чем а₍₁. Для корректировки числен­ных оценок альтернатив можно использовать как стандартную процедуру метода Черчмена-Акоффа, так и попарное сравнение предпочтительности альтернатив. Если численные оценки аль­тернатив не совпадают с представлением эксперта об их пред­почтительности, производится корректировка.

Метод фон Неймана—Моргенштерна. Он заключается в по­лучении численных оценок альтернатив с помощью так называ­емых вероятностных смесей. В основе метода лежит предполо­жение, согласно которому эксперт для любой альтернативы а-, менее предпочтительной, чем а₍, но более предпочтительной, чем a_t, может указать число а (0 <р < \) такое, что альтернатива а, эквивалентна смешанной альтернативе (вероятностной сме­си) [ pa_t, (l -р) а/]. Смешанная альтернатива состоит в том, что альтернатива a_f выбирается с вероятностью Р, а альтернатива а_{ с вероятностью \-Р. Очевидно, что если Р достаточно близко к 1, то альтернатива Oj менее предпочтительна, чем смешанная аль­тернатива [ pa_t, (\- p) a_t ]. В литературе помимо упомянутого выше предположения рассматривается система предположений (акси­ом) о свойствах смешанных и несмешанных альтернатив. К чис­лу таких предположений относятся предположение о связности и транзитивности отношения предпочтительности альтернатив, предположение о том, что смешанная альтернатива

х₂р₂ +... + x_Np_N > Xj/j + х₂р'₂ +... + x_n p ' _N.

Таким образом, устанавливается существование функции по­лезности

x_lPl +...+ x_Np_N,

значение которой характеризует степень предпочтительности

любой смешанной альтернативы, в частности и несмешанной.

Более предпочтительна та смешанная альтернатива, для которой

значение функции полезности больше.

Рассмотренные выше методы экспертных оценок обладают

различными качествами, но приводят в общем случае к близким результатам. Практика применения этих методов показала, что наиболее эффективно комплексное применение различных мето­дов для решения одной и той же задачи. Сравнительный анализ результатов повышает обоснованность делаемых выводов. При этом следует учитывать, что методом, требующим минимальных затрат, является ранжирование, а наиболее трудоемким метод последовательного сравнения (Черчмена Акоффа). Метод пар­ного сравнения без дополнительной обработки не дает полного упорядочения объектов.

МЕТОДЫ ТИПА ДЕЛЬФИ

Название методов экспертной оценки типа Дельфи связано с древнегреческим городом Дельфи, где при храме Аполлона с IX в. до н.э. до IV в. н.э. по преданиям находился Дельфийский оракул.

126

Глава 2

Предыдущая12345678910Следующая

Поделиться:

Воспользуйтесь поиском по сайту: