 |
Обработка результатов эксперимента
|
|
|
|
Таблица 3.1
Результаты экспериментальных исследований
| Номер пробы | VNaOH, мл | τ, мин. | Степень превращения, Х |
| 5… |
Степень превращения уксусной кислоты определяется по уравнению
,
где V1 - объем 0,5н NaOH, пошедший на титрование первой пробы;
V k – объем 0,5н NaOH, пошедший на титрование пробы за время τ.
Задание
1. По экспериментальным данным рассчитать степень превращения для каждой взятой пробы.
2.На основании экспериментальных данных построить графическую зависимость функции Х= f (τ) и определить равновесную степень превращения. Рассчитать для исследуемой реакции экспериментальную константу равновесия по уравнению и равновесный состав реагирующих веществ.
3. Рассчитать константу равновесия по термодинамическим данным (уравнение 2.20) и сравнить с экспериментальной константой равновесия.
4. Сделать вывод о вероятности протекания исследуемой реакции в прямом или обратном направлении и отметить все условия, которые позволить увеличить выход целевого продукта.
Правила безопасной работы
1. Перед началом эксперимента проверить включение вытяжного шкафа.
2. Следить за исправностью нагревательных приборов и электрических контактов.
3. Осторожно помещать уксусную и соляную кислоты в реактор.
4. В случае выхода установки из строя немедленно сообщить об этом лаборанту или преподавателю.
5. Подачу реагентов производить в присутствии лаборанта или преподавателя.
6. Контрольные вопросы
1. Ход работы и порядок расчетов.
2. Закон Гесса и следствия из него.
3. Зависимость теплового эффекта химической реакции от температуры.
|
|
|
4. Определение направления протекания обратимой реакции при заданных условиях.
5. Методы расчета константы равновесия.
6. Изобара Вант-Гоффа, изохора Вант-Гоффа, изотерма Вант-Гоффа.
7. Определение значения константы равновесия при другой температуре.
8. Определение константы равновесия идеальных и реальных газофазных процессов.
9. Определение константы равновесия жидкофазных химических процессов.
10.Показать на примере, каким образом можно определить равновесный состав обратимых химических реакций.
11. Методы экспериментального определения равновесного состава реакционной массы и константы равновесия.
12.Принцип Ле-Шателье.
13.Технологические приемы смещения равновесия.
Лабораторная работа № 4
ИССЛЕДОВАНИЕ КИНЕТИКИ РЕАКЦИИ
МЕТАЛЛОВ С КИСЛОТАМИ
ЦЕЛИ И ЗАДАЧИ РАБОТЫ
Цель работы: Экспериментальное изучение закономерностей топохимических процессов на примере реакции алюминия или цинка с кислотами при различных температурах.
Задачи:
– Знакомство с экспериментальными методами исследования топохимических реакций.
– Изучение методов определения лимитирующей стадии процесса и расчета активационных параметров по экспериментальным данным.
Знания: Студент должен знать теоретические основы топохимических процессов.
Умения: На основе полученных экспериментальных данных определить лимитирующую стадию процесса и рассчитать активационные параметры (константу скорости реакции, частотный фактор Аррениуса А, энергию активации).
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Химические реакции с участием газа (жидкости) и твердой фазы, сопровождающиеся возникновением или исчезновением твердой фазы, называются топохимическими. Можно указать много таких процессов, имеющих промышленное значение, например:
1) А (ТВ)+ В (Г) = С(ТВ) + Д Г(Ж).
Окисление пирита кислородом воздуха в производстве серной кислоты:
|
|
|
4FeS2(ТВ)+ 11O2 (Г) = 2Fe2O3 (ТВ) + 8SO2 (Г).
2) А (ТВ)+ В(Ж) = С(Г) + Е (ТВ).
Синтез ацетилена из карбида кальция:
CaC2(ТВ) + 2H2O(Ж) = C2H2(Г) + Ca(OH)2(ТВ).
3) А (ТВ)+ В(Ж) = С(ТВ) + Д (Ж) + Е (Г).
Разложение карбоната кальция под действием кислот:
CaCО3(ТВ) + H2SO4 (Ж) = CaSO4(ТВ) +H2O(Ж) + CO2(Г).
4) А (ТВ)+ В(Г) = Д (Г).
Горение угля:
С(ТВ) + O2(Г) = СO2(Г).
5) А (ТВ)+ В(Г) = С(ТВ).
Окисление металлов:
2Fe(ТВ) + 3/2O2(Г) = Fe2O3(ТВ).
Большинство топохимических процессов описываются моделью с невзаимодействующим ядром (рис. 2.1). Согласно модели с невзаимодействующим ядром, химическая реакция вначале протекает на внешней поверхности твердой частицы. Зона реакции постепенно продвигается внутрь ее, оставляя за собой полностью превращенный продукт (золу). Следовательно, в любой момент времени имеется частица твердого материала с постоянным объемом, которая включает в себя невзаимодействующее ядро твердого материала, размер которого в ходе реакции постоянно изменяется (уменьшается).
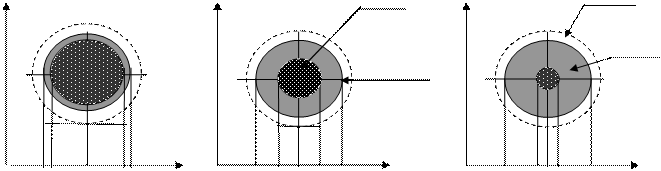Ств Ств 3 Ств 1
R R R
τ1 τ2 τ3
Рис 2.1. Модель частицы с невзаимодействующим ядром в различные моменты времени: τ1,τ2,τ3; (τ1 <τ2 <τ3); 1-газовая (жидкая) ламинарная пленка (ГЛП); 2-слой твердого продукта реакции («зола»); 3- ядро (исходный твердый реагент); 4-поверхность, на которой протекает химическая реакция
При анализе механизма процесса для частиц с невзаимодействующим ядром можно выделить 5 стадий развития процесса (рис 2.2.):
1)диффузию газообразного (жидкого) реагента через ГЛП к поверхности твердого вещества - (внешнедиффузионная область);
2)диффузию газообразного жидкого реагента через слой «золы» к поверхности реагента - (внутридиффузионная область);
3)химическое взаимодействие газообразного (жидкого) реагента с твердым реагентом - (кинетическая область);
А Г ВТ ВТ А Г
Рис. 2.2. Механизм процесса для модели с невзаимодействующим ядром
4)диффузию газообразных (жидких) продуктов через слой «золы» к по верхности частицы - (обратная внутренняя диффузия);
5)диффузию газообразных (жидких) продуктов реакции через ГЛП в основной поток газообразного (жидкого) реагента, окружающего частицу твердого реагента - (обратная внешняя диффузия).
|
|
|
В зависимости от лимитирующей стадии для топохимических процессов различают внешнедиффузионную, внутридиффузионную и кинетическую области протекания процесса.
Если сопротивление химической реакции и сопротивление переноса исходного реагента через слой «золы» будет значительно меньше сопротивления диффузии исходного реагента через ГЛП, считается, что топохимический процесс протекает во внешнедиффузионной области.
При внешнедиффузионной области протекания топохимической реакции для частиц сферической формы и одинакового размера (лимитирующими стадиями являются стадии 1, 5) процесс описывается кинетическим уравнением вида:
(2.1)
Если сопротивление диффузии жидкого (газообразного) реагента газовой пленке, окружающей ядро твердого реагента и сопротивление химической реакции на границе раздела фаз: исходное вещество – продукт значительно меньше, чем сопротивление через слой «золы», то общая скорость процесса лимитируется внутренней диффузией реагента через слой «золы».
Для внутренней диффузии (лимитирующими стадиями являются стадии 2), 4) в этом случае уравнение кинетики выглядит следующим образом:
(2.2)
Когда скорость топохимического процесса целиком определяется химической реакцией (лимитирующей стадией является стадия 3), то время пребывания твердого реагента в реакционной зоне, т.е. в кинетической области можно определить по формуле:
(2.3)
В уравнениях 2.1., 2.2., 3.3.:
rВ - мольная плотность вещества В, моль/см3;
nB - стехиометрический коэффициент при твердом веществе В;
R - радиус твердой частицы;
r - радиус невзаимодействующего ядра;
b - коэффициент массопередачи;
D - коэффициент диффузии;
k - константа скорости;
tn - время полного превращения твердого исходного реагента;
XB - степень превращения вещества В.
В данной работе рассматриваются топохимические реакции алюминия и цинка с водными растворами соляной и серной кислоты по следующей схеме:
A(Ж) + B(ТВ) = С(ТВ) + D(Г)
Основные реакции с участием алюминия и цинка с серной и соляной кислотами:
6HCl(Ж) + 2Al(ТВ) à 2А1Cl 3+ 3H2(Г) (1)
|
|
|
3H2SO4 (Ж) +2Al(ТВ)àА12(SO4)3 + 3H2(Г) (2)
2HCl (Ж) + Zn(ТВ) à ZnCl2 + H2(Г) (3)
H2SO4 (Ж) + Zn(ТВ) à Zn SO4 + H2 (Г) (4)
Кинетические зависимости топохимических процессов находят путем изучения характера изменения степени превращения твердого вещества, влияния размеров частицы и температуры реакции.
Взаимодействие металлов с кислотами представляет собой гетерогенный процесс, который характеризуется одновременным изменением нескольких параметров: уменьшением площади контакта металла с раствором, концентрации ионов водорода, изменением вязкости реакционной массы и ионной силы раствора. Одновременно происходит выделение большого количества тепла, что приводит к протеканию реакции в неизотермическом режиме.
Химическая сущность процесса получения на примере основных хлоридов алюминия сводится к гидролизу по схеме:
Аl+3 ↔ А1(ОН)2+ ↔ А1(ОН)+2 ↔ А1(ОН)3
Продукты гидролиза взаимодействуют между собой, образуя олигомерные гидроксосоединения:
2 А1(ОН)+2 ↔ [А12(ОН)4]2+
Гидролиз продолжается до равновесного состояния:
2[А12(ОН)4]2+ ↔ 2[А12(ОН)5]+
Этим ионам адекватно соответствуют наиболее устойчивые гидроксохлориды алюминия: Аl(ОН)Сl2, Аl(ОН)2Сl, Аl2(ОН)5Сl. Последний в этом ряду - пентагидроксохлорид алюминия является наиболее устойчивым. Атомное отношение Аl к Сl в нем составляет 1: 0,5. Он является наиболее эффективным коагулянтом в процессах водоочистки
Получение традиционного коагулянта сульфата алюминия проводят по реакции (2). Его получают взаимодействием разбавленного водного раствора серной кислоты с алюминием.
Получение гидроксохлоридов и сульфатов металлов можно отнести к топохимическим процессам, в результате которых исчезает исходная твердая фаза, т.е. для данных реакций характерны две области протекания процесса – это внешнедиффузионная область и кинетическая область.
Ме 1
2
С Со
Cп
R
Рис. 2.3. Схема топохимического процесса взаимодействия металла с кислотой: 1- жидкая ламинарная пленка (ЖЛП); 2- ядро (исходный металл); Сп –концентрация кислоты на поверхности металла; Со – концентрация кислоты в потоке; Me – металл
Обтекающий частицу поток жидкости интенсивно перемешан в объеме, так что концентрация кислоты постоянна и равна Со.
У поверхности частицы образуется пограничный слой жидкой пленки (на рисунке ограничен пунктиром).
Вещество переносится через жидкую пленку и это характеризуется коэффициентом массопередачи b. Для расчета b используют критериальные уравнения. Например, при обтекании одиночной частицы диаметром d:
Nu = 2+0.93Re0.5 Sc1/3, (2.4)
где критерий Нуссельта Nu = bd/D; критерий Рейнольдса Re = ud/ν. критерий Шмидта Sc = ν/D, где D – коэффициент диффузии; u – скорость потока; ν – вязкость раствора.
|
|
|
При анализе этого процесса можно выделить следующие этапы процесса:
1) перенос кислоты из потока к поверхности, при этом концентрация кислоты у поверхности Сп должна быть меньше, чем в потоке; распределение концентраций показано на рис. 2.3.;
2) реакция кислоты с металлом на наружной поверхности частицы;
3) перенос продукта реакции (водорода и соответствующей соли) от поверхности в поток. При этом можно предположить, что скорость реакции не зависит от концентрации продукта и его отвод от поверхности не влияет на процесс.
Математическая модель включает описание изменения (уменьшение) размеров твердых частиц и концентрации веществ в растворе. Уменьшение размера частицы происходит гораздо медленнее, чем устанавливается распределение концентраций в пограничном слое; так что в каждый момент времени процессы в жидкой фазе можно считать стационарными. В стационарном режиме поток жидкой фазы к поверхности (W1) и скорость реагирования (W2) равны:
W1=W2. (2.5)
Поток жидкой фазы пропорционален поверхности частицы Sr радиуса r и разности концентраций кислоты в потоке Со и у поверхности Сп.
W1= -b Sr(Co-Cп). (2.6)
На поверхности протекает реакция псевдопервого порядка, а скорость превращения кислоты пропорциональна наружной поверхности частицы
W2 = -k Cп Sr.. (2.7)
Подставляя (2.6) и (2.7) в (2.4), получим:
b (Co- Cп) = k Cп.. (2.8)
Далее определяем концентрацию кислоты у поверхности:
Сп = Со/ (1+k/b). (2.9)
И наблюдаемую скорость превращения:
Wн = - k Cп = - kCo/(1+k/b). (2.10)
Комбинацию параметров k и b обозначим Кн - наблюдаемая константа скорости:
Кн = k/(1+k/b). (2.11)
Далее Wн =Кн Со. (2.12).
Видно, что Wн представлена как реакция первого порядка, но Кн не имеет физического смысла, а является параметром, зависящим от условий процесса.
Изменение количества твердого компонента N в единицу времени равна скорости его превращения на наружной поверхности частицы:
dN/dτ = wв Sr. (2.13)
Скорости превращения веществ связаны стехиометрическим соотношением wв/νв = wa/νa. В рассматриваемой реакции (например. схема 4) νв = νа и wв = wа = -kCп = -Кн Со.
Количество твердого компонента в единице объема обозначим no. Для непористой частицы n0 = ρ/М, где М - молекулярная масса твердой частицы, ρ – плотность твердой частицы.
За время dτ прореагирует тонкий поверхностный слой толщиной dr, в котором содержится dN = no Sr dr реагента В. Уравнение (2.13) преобразуем к виду:
no Sr (dr/dτ) = - Кн Со Sr и далее dr/dτ = - Кн (Со/no). (2.14)
Интегрируя (2.14) в пределах от начального момента времени τ = 0 (размер частицы первоначальный, т.е. R) до момента r (размер частицы уменьшается до r), получим
R – r = Кн (Со/no)τ (2.15)
Через некоторое время τп твердая частица прореагирует полностью, т.е. в этот момент r =0. Время полного превращения найдем из (2.15).
τп= R no/ (Кн Со). (2.16)
Введя безразмерный радиус р = r/R и используя выражение (2.16), приведем (2.15) к безразмерному виду:
р = 1- τ/τп. (2.17).
На практике превращение удобно выразить через степень превращения твердого: Хв = (No- N)/No. Количество твердого в первоначальной частице составляет No = (4/3)πR3 n0 и в текущей момент N = (4/3)πr3 n0, откуда получим
Хв= 1-р3 и р = (1- Хв)1/3 (2.18).
Изменение степени превращения со временем:
Хв = 1-(1- τ/τп)1/3 (2.19)
Можно найти, как будет меняться со временем наблюдаемая скорость превращения, отнесенная к одной частице.
Vн(част) = Vн Sr = Vн 4πr2 = -4 πR2o Кн Со (1- τ/τп)2 (2.20)
Определение области протекания реакции является важнейшим процессом для гетерогенных реакций, которое позволяет получить соответствующую кинетическую модель, необходимую при расчете реакторов.
|
|
|
