 |
Основные компоненты моделей массового обслуживания
|
|
|
|
МОДЕЛИ МАССОВОГО ОБСЛУЖИВАНИЯ
Массовое обслуживание в коммерческой деятельности
Коммерческая деятельность малого и среднего бизнеса связана с выполнением множества операций на этапах движения товарной массы из сферы производства в сферу потребления. Такими операциями являются погрузка товаров, перевозка, разгрузка, хранение, обработка, фасовка, реализация и т.д., время выполнения и возникновение которых носит случайный характер.
Это создает неравномерность в работе, порождает недогрузки, простои и перегрузки в коммерческих операциях. Одним из проявлений недостатков - очереди, например, посетителей в кафе, столовых, ресторанах, водителей автомобилей на товарных базах, ожидающих разгрузки, погрузки или оформления документов.
Пример. Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, он начинает обслуживать покупателя сразу, если покупателей несколько, выстраивается очередь.
Перечисленные задачи можно успешно решать с помощью методов и моделей специально созданной для этих целей теории массового обслуживания (ТМО), использующей аппарат теории вероятностей и математической статистики, дифференциальных уравнений и численных методов. Основоположником ее стал датский ученый А.К.Эрланг, исследовавший проблемы функционирования телефонных станций.
Любой запрос на удовлетворение какой-либо потребности будем называть заявкой (требованием). Например, заявками, нуждающимися в обслуживании, являются покупатели в магазинах, заявки на телефонные разговоры, заявки на получение товара и т.д.
Под обслуживанием заявок будем понимать удовлетворение потребности. Поступившие заявки нуждаются в обслуживании со стороны какого-либо устройства (человека, группы людей, технического устройства).
|
|
|
Совокупность средств, которые осуществляют обслуживание заявок, называется каналом обслуживания (КО).
Совокупность каналов обслуживания называется обслуживающей системой.
Заявки на обслуживание образуют потоки, которые до выполнения операций обслуживания называются входящими, а после возможного ожидания начала обслуживания, т.е. простоя в очереди, образуют потоки обслуживания в каналах, а затем формируется выходящий поток заявок.
В целом совокупность элементов входящего потока заявок, очереди, каналов обслуживания и выходящего потока заявок образует систему массового обслуживания - СМО
Рис. 1. Структурная схема СМО
Способы расположения КО: параллельное расположение каналов обслуживания
последовательное расположение каналов обслуживания. В таких системах процесс обслуживания носит многофазовый характер, обслуживание заявки одним каналом называется фазой обслуживания.
Работу системы обслуживания характеризуют такие показатели:
· время ожидания начала обслуживания;
· длина очереди;
· возможность получения отказа в обслуживании;
· среднее число занятых КО;
· общая продолжительность нахождения заявки в СМО и т.д.
Для построения СМО необходимо иметь:
· описание входящего потока заявок (требований);
· описание способа обслуживания заявок;
· описание дисциплины очереди, т.е. указание того, каким образом требования поступают из очереди на обслуживание;
· число КО;
· производительность КО.
Основные компоненты моделей массового обслуживания
СМО - это модели таких систем, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания со случайным временем обслуживания.
|
|
|
Примерами систем массового обслуживания могут служить:
1. станции технического обслуживания автомобилей;
2. персональные компьютеры, обслуживающие поступающие заявки или требования на решение тех или иных задач;
3. аудиторские фирмы;
4. отделы налоговых инспекций, занимающиеся приемкой и проверкой текущей отчетности предприятий;
5. телефонные станции и т. д.
Потоки событий. Поток событий – это последовательность событий, происходящих одно за другим (следующих одно за другим) в случайные моменты времени. Например, поток телефонных вызовов на АТС, поток ж.д. составов, поступающих на сортировочную станцию, поток покупателей в магазине и т.д.
События, образующие поток, в общем случае могут быть различными. Потоки однородных событий, различаются лишь моментами появления. Такой поток можно изобразить в виде последовательности точек на временной оси 
, которые соответствуют моментам появления событий.
Потоки событий - регулярные, с лучайные
· Стационарный поток событий, характеризуется постоянная интенсивностью 
событий - среднее число событий в единицу времени.
· Поток событий называется потоком без последействия, если для любых неперекрывающихся участков времени 
и 
число событий, попадающих на один из них, не зависит от числа событий, попадающих на другой.
· Поток событий называется ординарным, если вероятность попадания на элементарный временной интервал двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Это свойство означает, что заявки поступают на вход СМО поодиночке, а не парами, тройками и т.д.
Поток событий, обладающий тремя указанными свойствами (стационарностью, ординарностью, не имеющим последействия), называется простейшим или стационарным пуассоновским потоком.
Число событий, попадающих на любой фиксированный интервал времени 
, будет распределено по закону Пуассона:
. (1)
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны среднему числу событий 
за промежуток 
.
Функция распределения вероятностей случайного интервала 
, (2)
которая называется показательной или экспоненциальной.
|
|
|
Плотность вероятностей
. (3)
Величина 
называется параметром показательного закона.
Дисциплина очереди
· первым пришел — первый обслуживаешься;
· пришел последним — обслуживаешься первым;
· случайный отбор заявок;
· отбор заявок по критерию приоритетности;
· ограничение времени ожидания
Механизм обслуживания.
Характеристики обслуживания:
· продолжительность процедуры обслуживания,
· пропускная способность - количество требований, одновременно обслуживаемых в результате выполнения каждой такой процедуры
В 
- канальной системе пропускная способность равна 
.
Под длительностью обслуживания заявки обычно понимают интервал между моментом поступления заявки в КО и моментом выхода заявки из КО.
На практике считают длительность обслуживания распределенной по экспоненциальному закону
,
где 
- среднее число требований, обслуживаемых в единицу времени (интенсивность обслуживания).
Поведение СМО. Под состоянием СМО понимается число находящихся в системе заявок как стоящих в очереди, так и находящихся в КО.
СМО относится к системам с конечным или счетным множеством состояний (с дискретными состояниями).
Рассмотрим систему со счетным множеством состояний 
.
Обозначим через 
вероятность того, что в момент 
система будет находиться в состоянии 
(вероятность 
- состояния).
Для любого 
выполняется условие нормировки 
.
Марковские СП с дискретными состояниями и непрерывным временем. Процесс, протекающий в системе, называется марковским (процессом без последействия), если вероятность любого состояния СМО в последующий момент времени зависит только от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние.
Случайный марковский процесс с дискретными состояниями и непрерывным временем еще называется марковской цепью, которую можно описать вероятностями состояний 
и вероятностями переходов 
из состояния 
в состояние 
. Вероятности переходов можно представить двумя способами:
|
|
|
- в виде матрицы переходов 
где сумма элементов каждой строки обязательно должна равна единице;
- в виде графа, вершины которого соответствуют состояниям системы, а дуги указывают возможные переходы из одного состояния в другое. Сумма вероятностей для дуг, выходящих из любой вершины графа должна равняться 1.
Предположим в момент времени 
система находится в состоянии 
с вероятностью 
. При этом 
представляют собой вероятности того, что в момент 
система окажется в состояние 
, если в момент 
была в состоянии 
. Тогда вероятность того, что в момент 
система окажется в состоянии 
, определяется формулой полной вероятности
(6)
Уравнения Колмогорова.
Рассмотрим, например, процесс обслуживания в газетном киоске: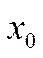 
- состояние, когда киоскер простаивает;
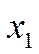- состояние, когда киоскер (КО) занят обслуживанием;
- состояние, когда один покупатель приобретает газеты, а другой стоит в очереди.
Переход СМО из 
в 
происходит под воздействием потока покупателей (заявок) интенсивностью 
, а из состояния 
в -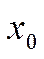 
система переводится потоком обслуживания с интенсивностью 
и т.д.
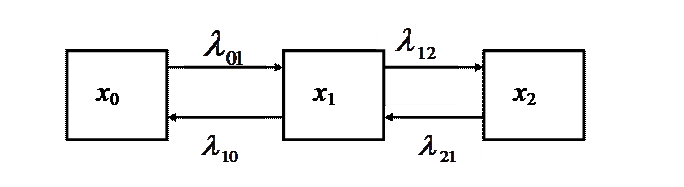
Рассмотрим математическое описание процесса в СМО на примере газетного киоска. СМО имеет три состояния 
.
Полагаем, что все переходы СМО происходят под воздействием простейших потоков событий с интенсивностями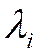 
. Обозначим через 
вероятность того, что в момент времени система находится в состоянии 
. Очевидно, что 
сумма вероятностей всех состояний СМО равна 1 по условию нормировки
. (7)
Рассмотрим состояние 
СМО 
.
, определим вероятность того, что в момент 
система будет находиться в состоянии 
.
В соответствие с (6)
. (8)
Определим переходные вероятности, считая потоки заявок простейшими
.
Условная вероятность 
-
Эту вероятность 
можно рассматривать, как вероятность того, что за время 
не поступило ни одной заявки 
. (9)
. (10)
Вероятность 
. Другими словами, за время 
произойдет хотя бы одно событие (придут 1, 2, 3 и т.д. заявок). Вероятность этого явления равна:
. (11)
С учетом (10), (11) формула (8) принимает вид
. (12)
(12а)
Используем предельный переход в (12а) ДУ для 
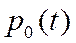
. (13)
Теперь запишем ДУ для вероятности состояния
(13a)
а) СМО в момент времени 
с вероятностью 
находилась в состоянии и за малое время 
так и не перешла в другое соседнее состояние 
или 
. Следовательно, потоки с интенсивностям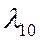и 
и 
не содержали заявок за время 
, т.е.
. (14)
б) Система находилась в состоянии 
и за время 
перешла в 
. Переход произошел под воздействием потока интенсивностью 
с вероятностью
|
|
|
. (15)
в) Система находилась в состоянии 
и за время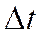 
перешла в состояние 
под воздействием простейшего потока с интенсивностью 
с вероятностью
.
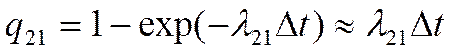Тогда в соответствии с (13a) получаем
(16)
Переходя к пределу в нем при 
, получим ДУ
. (17)
Проведя аналогичные рассуждения для состояния СМО 
, получим систему ДУ, которые называются уравнениями А.Н. Колмогорова
(18)
Систему (18) следует дополнить условием нормировки
.
Сформулируем общее правило составления уравнений.
· В левой части каждого из них находится производная вероятности состояния 
СМО;
· В правой части – сумма произведений вероятностей всех состояний СМО, из которых потоки переводят систему в данное состояние, на интенсивность соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, на вероятность данного 
состояния.
Система (18) представляет собой систему ЛДУ с постоянными коэффициентами. Для нахождения решения Коши системы (18) надо задать начальные условия
Режимы функционирования СМО:
· переходный;
· стационарный (установившийся)
- финальные вероятности
(19)
(20)
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то финальные (предельные) вероятности существуют.
.
|
|
|
