 |
Одноканальная модель СМО с отказами
|
|
|
|
Одноканальная СМО с отказами. Входящий поток и поток обслуживания являются простейшими с интенсивностями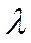 
и 
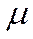соответственно.
Представим данную систему массового обслуживания в виде графа (рис.3), у которого имеются два состояния:
- 
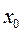- КО свободен (ожидание);
- 
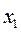- канал занят (идет обслуживание заявки).
Рис.3
Обозначим вероятности состояний: P 0(t) - вероятность состояния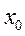 
-«канал свободен»; P 1(t) - вероятность состояния 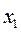- «канал занят». По графу состояний составим систему дифференциальных уравнений Колмогорова для вероятностей состояний:
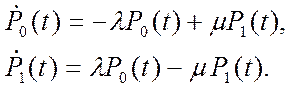(22)
Система линейных дифференциальных уравнений (22) имеет решение с учетом нормировки P 0(t) + P 1(t) = 1 и начальных условий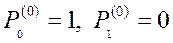 
. В результате для 
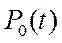имеем
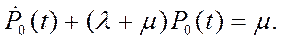(23)
Характеристическое уравнение имеет один корень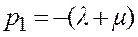 
. Свободная составляющая, определяемая ненулевыми начальными условиями, принимает вид
Вынужденная составляющая вероятности повторяет структуру правой части (23)
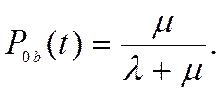
Общее решения ДУ записывается в форме
Постоянная интегрирования при данных НУ равна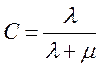 
.
Решение данной системы определяет переходный режим работы, поскольку оно зависит от t
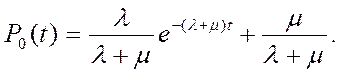(24)
По истечении большого интервала времени (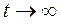
) достигается стационарный (установившийся) режим:
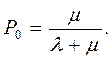- финальная вероятность состояния 
(25)
Для одноканальной СМО с отказами вероятность P 0 есть относительная пропускная способность системы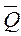 
. 
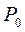- вероятность того, что канал свободен, т. е. 
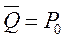. Зная относительную пропускную способность, можно найти абсолютную. Абсолютная пропускная способность (Q) - среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:
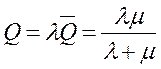. (26)
Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал занят»:
|
|
|
Величина 
может быть интерпретирована как средняя доля необслуженных заявок среди поданных.
Пример. Диагностический автоцентр с одной линией обслуживания представляет собой одноканальную СМО.
Поток прибывающих автомобилей распределен по закону Пуассона и имеет интенсивность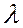 
= 0,85 (автомобиля в час).
Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.
Требуется определить характеристики центра диагностики, работающего в стационарном режиме.
Решение
1. Интенсивность потока обслуживания автомобилей:
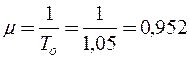
2. Коэффициент загрузки
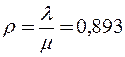
Длина очереди на диагностику не ограничена.
Требуется определить следующие характеристики:
· вероятности состояний центра диагностики;
· среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);
· среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);
· среднее число автомобилей в очереди на обслуживании;
· среднюю продолжительность пребывания автомобиля в очереди.
1. 
=0,952;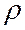 
=0,893.
2. Вычислим финальные вероятности системы по формулам
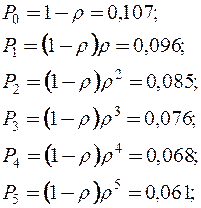
и т.д.
P 0(t) определяет долю времени (10,7%), в течение которого центр диагностики простаивает.
3. Среднее число автомобилей, находящихся в системе (на обслуживании и в очереди):
4. Средняя продолжительность пребывания машины в центре:
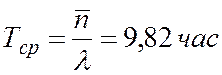
5. Среднее число автомобилей в очереди на обслуживание:
6. Средняя продолжительность пребывания автомобиля в очереди:
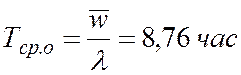
7. Относительная пропускная способность системы:
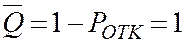
т. е. каждая заявка, пришедшая в систему, будет обслужена.
8. Абсолютная пропускная способность:
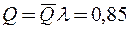
Длина очереди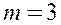 
9. Финальные вероятности СМО с ограниченной очередью:
, 
10. Вероятность отказа в обслуживании автомобиля:
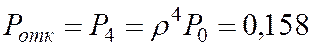
11. Относительная пропускная способность поста диагностики:
|
|
|
.
12. Абсолютная пропускная способность поста диагностики
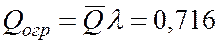автомобиля в час
|
|
|
