 |
Анализ систем массового обслуживания
|
|
|
|
2.1. Одноканальная СМО с неограниченной очередью
В коммерческой деятельности встречается немало экономических процессов, описываемых данной моделью. Рассмотрим работу погрузочного пункта.
Автомашины прибывают случайным образом с интенсивностью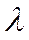 
, т.е. за один час в среднем прибывает 
машин. Среднее время между прибытием машин равно 
. Распределение моментов прибытия является пуассоновским. Это означает, что вероятность прибытия в промежутке 
ровно 
машин определяется формулой Пуассона
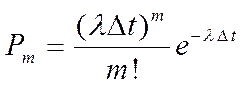, (1)
где 
- среднее число машин за интервал 
.
На погрузочном пункте автомашины обслуживаются со средней интенсивностью 
, т.е. среднее время обслуживания составляет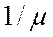 
час. Длительность обслуживания характеризуется показательным распределением
. (2)
Кроме того, машины обслуживаются по принципу «Первым прибыл – первым обслуживаешься». Ограничений на длину очереди не накладывается.
Требуется определить финальные вероятности состояний СМО, а также некоторые характеристики ее эффективности.
Решение. Состояние СМО будем обозначать через 
, если на погрузочном пункте находится 
грузовиков, как обслуживаемых, так и ожидающих обслуживания:
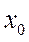- КО свободен (на погрузочном пункте нет машин);
- КО занят, очереди нет;
- КО занят, одна машина стоит в очереди;
- - - - - - - - - - - - - - - - - - - - - - - -
- КО занят,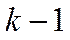 
машина стоит в очереди.
СМО переходит в 
состояние, когда прибывает следующая машина и в состояние 
, когда заканчивается обслуживание одной машины (машина загружена).
Построим граф состояний СМО, учитывая при этом, что одновременно не происходит двух и более изменений состояний СМО.
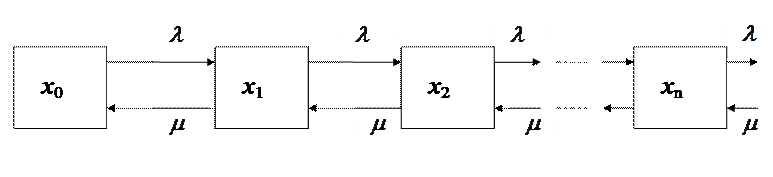Рис.1
.
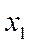
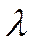Тот же поток переводит СМО из состояния 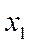в состояние 
, из 
в 
и т.д.
|
|
|
, …, 
, 
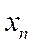
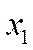Следовательно, поток обслуживания в этом случае имеет интенсивность 
и одинаков везде.
Составим уравнения Колмогорова, руководствуясь известным правилом:
· в левой части уравнения находятся производные вероятностей состояний 
;
· в правой части – сумма произведений вероятностей всех состояний, из которых возможен переход в данное состояние, на интенсивности соответствующих потоков минус суммарная интенсивность всех потоков, выводящих СМО из данного состояния, на вероятность этого состояния
(3)
Для отрицательных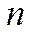 
вероятность состояний равна нулю.
Финальные вероятности для такой СМО существуют не всегда, а только когда система не перегружена. Тогда
(4)
Из (4) имеем
и т.д.
В общем случае 
получаем
. (5)
Величина 
называется коэффициентом загрузки системы или коэффициентом использования системы. Он показывает среднее число заявок, приходящих за среднее время обслуживания одного требования.
В силу условия нормировки
. (6)
Ряд в скобках представляет собой бесконечную геометрическую прогрессию с знаменателем 
. При 
ряд расходится, финальные вероятности не существуют, говорят СМО перегружена. При 
ряд является сходящимся, что указывает на существование финальных вероятностей. Суммируя в (6) при , получаем
. (7)
Вероятности 
определяются в соответствие с формулой (5)
(8)
Эти вероятности, в свою очередь, образуют геометрическую прогрессию со знаменателем . Как ни странно, максимальная среди них вероятность 
того, что КО свободен.
Показатели эффективности СМО.
· Среднее число требований, находящихся в системе (машин на погрузочном пункте)
, т.к. 
. (9)
Подставим (8) в (9)
.
Вынесем 
за пределы суммы
.
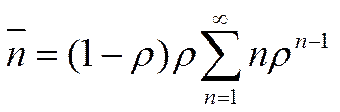Заметим, что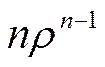 
есть производная 
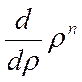. Поэтому
. (10)
Сумма в (10) представляет бесконечную убывающую геометрическую прогрессию с первым членом и знаменателем . Эта сумма равна 
, а ее производная - 
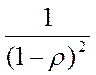. С учетом этого получаем
|
|
|
. (11)
· Среднее число заявок в очереди (среднее число автомашин, ожидающих обслуживания).
(12)
· Среднее время пребывания заявки в системе (на погрузочном пункте) – равно среднему интервалу между прибытиями машин, умноженному на среднее число заявок в системе
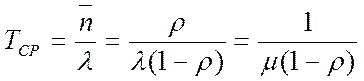. (13)
· Среднее время пребывания заявки в очереди
. (14)
Из анализа простой СМО следует, что при малой интенсивности обслуживания 
образуется большая очередь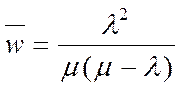 
. С другой стороны высокая интенсивность обслуживания может привести к недогруженности системы в некоторые периоды. Для принятия правильного решения следует ввести экономические показатели, например, в форме затрат, возникающих при работе погрузочного пункта.
Обозначим через 
издержки, связанные с обслуживанием одной машины, а через 
- потери в единицу времени, обусловленные пребыванием (простоем) транспорта в системе. Тогда величина 
характеризует расходы по обслуживанию среднего числа машин 
в единицу времени, а 
- средние потери, связанные с простоем 
машин в течение единицы времени. Общие затраты, обусловленные работой пункта, равны
. (15)
Очевидно, следует организовать работу погрузочного пункта с такой интенсивностью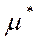 
, чтобы сделать суммарные расходы (15) минимальными.
ММО в управлении запасами. Поступление товаров в магазин с интенсивностью 
и имеет пуассоновское распределение. Покупатели прибывают в магазин с 
.
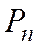- вероятность наличия в магазине 
- единиц товара;
-
КО – потребители
Затраты на организацию и управление запасами
Минимум потерь достигается путем оптимизации интенсивности заказов 
2.2. Одноканальная СМО с ограниченной длиной очереди
(СМО с ожиданием)
В коммерческой деятельности, в малом и среднем бизнесе часто встречаются СМО с ограниченной длиной очереди.
Пример - магазин самообслуживания, где поток покупателей является простейшим с интенсивностью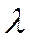 
. В магазине установлен один кассовый аппарат, позволяющий в среднем обслуживать 
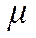покупателей в единицу времени. Определим характеристики СМО при условии, что очередь ограничена 
покупателями.
Заявки, поступившие в момент, когда все места в очереди заняты, к обслуживанию не принимаются и покидают систему. Длительности обслуживания распределены по экспоненциальному закону.
|
|
|
Граф СМО показан на рис. 2. Состояния СМО можно представить следующим образом
- КО свободен;
- КО занят, очереди нет;
- КО занят, одна заявка стоит в очереди;
- - - - - - - - - - - - - - - - - - - - - - - -
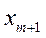- КО занят, в очереди все 
мест заняты, любая следующая заявка получает отказ.
Рис. 2
Описание процессов в СМО. Финальные вероятности состояний СМО имеют вид
(16)
. (17)
Учитывая, что правая часть (17) представляет собой конечную геометрическую прогрессию, это выражение приводится к виду
. (18)
Эта формула справедлива для всех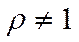 
. Если же 
, то согласно (16) 
, т.е. вероятности всех состояний СМО равны.
Отсюда
.
Следует отметить, что выполнение условия стационарности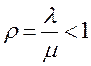 
для данной СМО не обязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать 
), а не соотношением между интенсивностями входного и обслуживающего потоков 
.
Показатели эффективности СМО.
· Среднее число заявок в системе
.
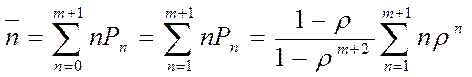(19)
· Среднее число заявок в очереди (средняя длина очереди) – определяется математическим ожиданием случайного количества заявок в очереди. Число заявок в очереди на единицу меньше числа заявок в системе. Отсюда следует
. (20)
· Среднее время пребывания заявки в системе – равно среднему интервалу между поступлениями требований, умноженному на среднее число заявок в системе
.
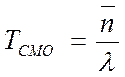· Среднее время пребывания заявки в очереди
.
· Вероятность отказа. Заявка получает отказ, если она поступает в момент времени, когда СМО находится в состоянии 
, т.е. все места в очереди заняты. Поэтому вероятность отказа определяется вероятностью того 
, что СМО находится в состоянии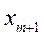 
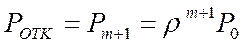. (21)
· Относительная пропускная способность СМО характеризуется вероятностью того, что поступившая заявка будет обслужена. Это событие противоположно отказу, следовательно
|
|
|
.
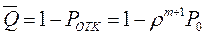· Абсолютная пропускная способность СМО
.
|
|
|
