 |
Среда моделирования GPSS World
|
|
|
|
GENERATE (EXPONENTIAL (1,0,1/0.85))
QUEUE REM
SEIZE 1
DEPART REM
ADVANCE (EXPONENTIAL (1,0,1.05))
RELEASE 1
TERMINATE 1
- GENERATE A,B - генерирование требования в системе.
- QUEUE А (очередь) - вход требования в очередь
- SEIZE А (занять) - определение занятости канала обслуживания. Если канал занят, то требование остается в очереди, если свободен - то входит в канал обслуживания.
- DEPART А (выйти) - выход требования из очереди.
- ADVANCE А,В (задержать) -обслуживание требования в канале обслуживания
- RELEASE (освободить) - Освобождение канала обслуживания
- TERMINATE А (завершить) - Выход требования из системы
GENERATE (EXPONENTIAL(1,0,1/0.85))
QUEUE REM
SEIZE 1
DEPART REM
ADVANCE (EXPONENTIAL(1,0,1.05))
RELEASE 1
TERMINATE 1
2.4. Многоканальная (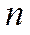 - канальная) СМО с неограниченной
- канальная) СМО с неограниченной
Очередью
Постановка задачи. Например, в расчетном блоке супермаркета установлено 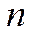 кассовых аппаратов, которые могут обслуживать одновременно
кассовых аппаратов, которые могут обслуживать одновременно 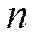 покупателей (заявок).
покупателей (заявок).
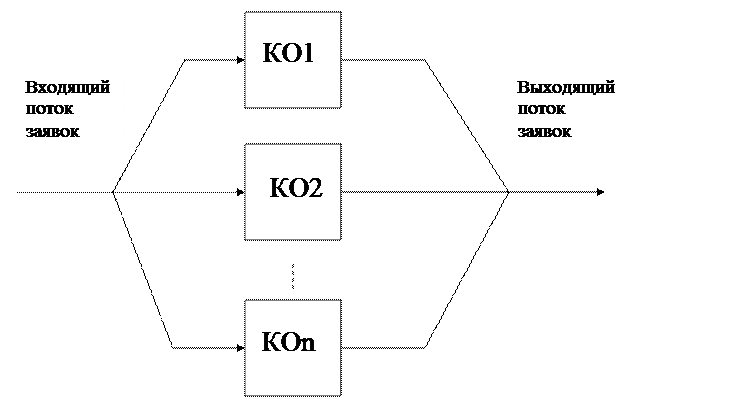
Интенсивность входного потока покупателей составляет 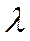 человек в единицу времени. Интенсивность обслуживания клиентов каждым КО одинакова и равна
человек в единицу времени. Интенсивность обслуживания клиентов каждым КО одинакова и равна 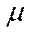 . Средняя продолжительность обслуживания одной заявки -
. Средняя продолжительность обслуживания одной заявки - 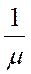 . Входящий и обслуживающий потоки являются простейшими пуассоновскими. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, причем длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону распределения.
. Входящий и обслуживающий потоки являются простейшими пуассоновскими. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, причем длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону распределения.
Конечная цель использования 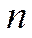 параллельно включенных обслуживающих каналов заключается в повышении (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно
параллельно включенных обслуживающих каналов заключается в повышении (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно 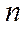 клиентов.
клиентов.
|
|
|
Определить финальные вероятности состояний и основные характеристики СМО.
Решение:
Состояние СМО определяется числом заявок, находящихся в системе:
- 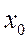 -заявок нет, все каналы свободны;
-заявок нет, все каналы свободны;
- 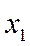 - занят один канал, остальные свободны;
- занят один канал, остальные свободны;
- ………………………………………………….
- 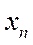 - заняты все
- заняты все 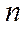 каналов, очереди нет;
каналов, очереди нет;
- ………………………………………………….
- 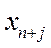 - заняты все n каналов,
- заняты все n каналов, 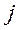 заявок в очереди.
заявок в очереди.
Граф состояний многоканальной системы массового обслуживания с неограниченной очередью имеет вид, показанный на рис.1.

Рис. 1
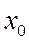
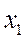
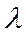
Оценим интенсивность потока обслуживания. Пусть СМО находится в состоянии 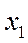 (работает один КО). Он производит
(работает один КО). Он производит 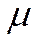 обслуживаний в единицу времени. Значит интенсивность потока, переводящего СМО из состояния
обслуживаний в единицу времени. Значит интенсивность потока, переводящего СМО из состояния 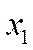 в
в 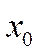 , равна
, равна 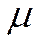 .
.
Состояние 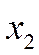 (работают два КО). Для перевода СМО в состояние
(работают два КО). Для перевода СМО в состояние 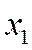 нужно, чтобы либо закончил обслуживание первый КО, либо второй канал. Суммарная их интенсивность равна
нужно, чтобы либо закончил обслуживание первый КО, либо второй канал. Суммарная их интенсивность равна 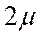 . Следовательно, из
. Следовательно, из 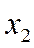 в
в 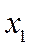 система переходит под действием как бы двух потоков с суммарной интенсивностью
система переходит под действием как бы двух потоков с суммарной интенсивностью 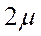 и т.д. Для перевода СМО из любого состояния
и т.д. Для перевода СМО из любого состояния 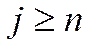 в состояние с меньшим индексом используются потоки с интенсивностью
в состояние с меньшим индексом используются потоки с интенсивностью 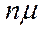 .
.
Уравнения Колмогорова для этого графа
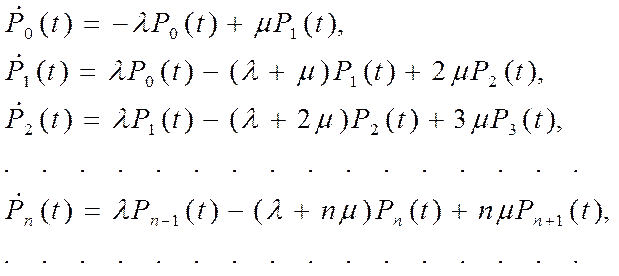 (26)
(26)
Система (26) носит название уравнений Эрланга – в честь основателя ТМО. Финальные вероятности в стационарном режиме принимают вид
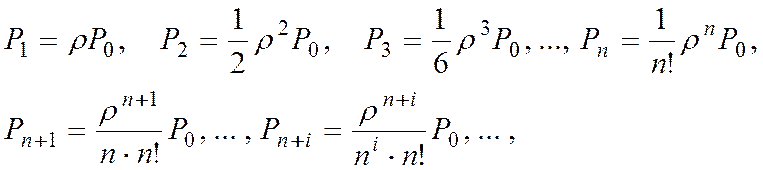 (27)
(27)
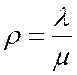
Полученные выражения называются формулами Эрланга. Из условия нормировки 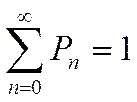 получаем
получаем
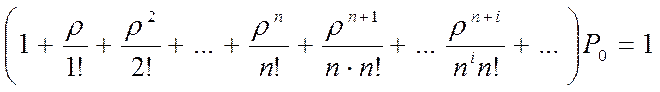 . (28)
. (28)
Рассмотрим совокупность стоящих в скобках членов, начиная с 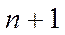 , т.е.
, т.е.
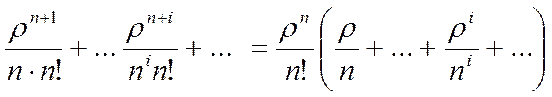 .
.
Последовательность в скобках представляет собой геометрическую бесконечную прогрессию, которая при 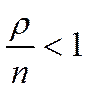 будет убывающей. Ее сумма при первом члене
будет убывающей. Ее сумма при первом члене 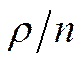 и таком же знаменателе будет равна
и таком же знаменателе будет равна
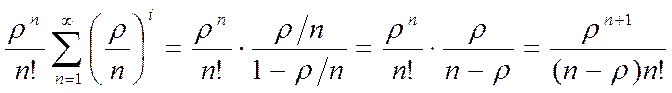 . (29)
. (29)
Следовательно, в данной модели финальные вероятности существуют при 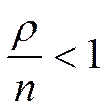 . Если
. Если 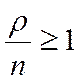 , очередь растет до бесконечности. Условие нормировки с учетом (29) запишется
, очередь растет до бесконечности. Условие нормировки с учетом (29) запишется
 . (30)
. (30)
Из (30) находим
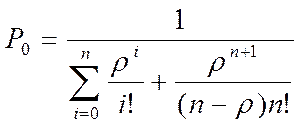 . (31)
. (31)
|
|
|
Показатели эффективности СМО
· Среднее число заявок в очереди (средняя длина очереди)
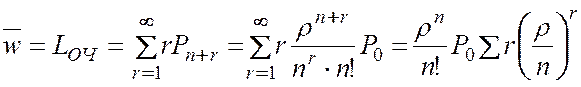 .
.
Используя подход с дифференцированием, рассмотренный в предыдущем параграфе
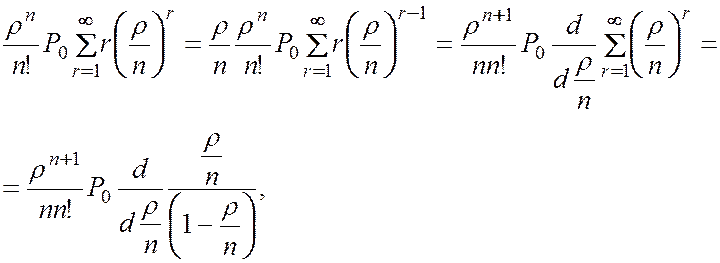
получаем при 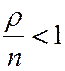
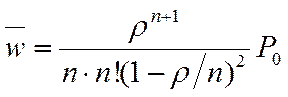 . (32)
. (32)
· Вероятность отказа в такой СМО равна 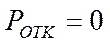 .
.
· Относительная пропускная способность СМО 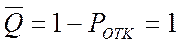 .
.
· Абсолютная пропускная способность СМО 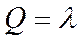 .
.
· Среднее число занятых КО. Абсолютная пропускная способность СМО определяет среднее число обслуживаемых заявок в единицу времени. Каждый занятый КО в единицу времени в среднем обслуживает 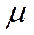 заявок. Значит среднее число занятых каналов равно
заявок. Значит среднее число занятых каналов равно
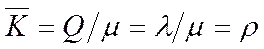 .
.
· Среднее число заявок в СМО
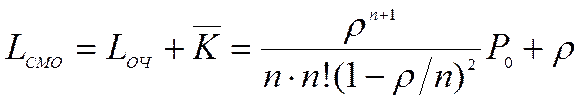 . (33)
. (33)
· Среднее время ожидания в очереди
Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.
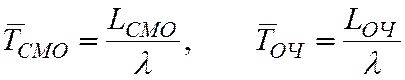 . (34)
. (34)
Для данной системы имеем
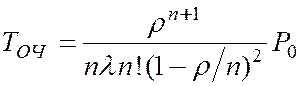 .
.
· Среднее время нахождения в системе
 .
.
Формулы (34) называются формулами Литтла. Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее: оба потока заявок имеют одну и ту же интенсивность  .
.

Х(t)—число заявок, прибывших в СМО до момента T, Y(t) — число заявок, покинувших СМО до момента T
И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (У(t)). Обе линии — ступенчатые, верхняя — X(t), нижняя — Y(t).
Очевидно, что для любого момента t их разность Z(t) = Х(t) —Y(t) есть не что иное, как число заявок, находящихся в СМО. Когда линии X(t) и У(t) сливаются, в системе нет заявок.
Рассмотрим большой промежуток времени Т и вычислим для него среднее число заявок, находящихся в СМО:
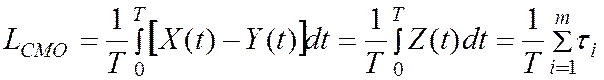
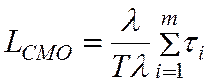
Величина Тl есть не что иное, как среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен 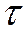 на среднее число заявок, то получим среднее время пребывания заявки в системе
на среднее число заявок, то получим среднее время пребывания заявки в системе 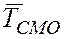 .
.
Итак, 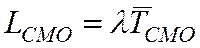
Пример. Механическая мастерская завода имеет три бригады рабочих, занимающихся ремонтом техники. Поток неисправной техники, прибывающей в мастерскую - пуассоновский и имеет интенсивность 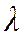 = 2,5 единицы техники в сутки, время ремонта одной единицы распределено по показательному закону со средним значением, равным
= 2,5 единицы техники в сутки, время ремонта одной единицы распределено по показательному закону со средним значением, равным 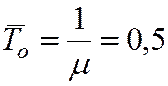 сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь техники перед мастерской может расти практически неограниченно.
сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь техники перед мастерской может расти практически неограниченно.
|
|
|
Требуется вычислить следующие характеристики системы:
- финальные вероятности состояний системы;
- среднее число заявок в очереди на обслуживание;
- среднее число находящихся в системе заявок;
- среднюю продолжительность пребывания заявки в очереди;
- среднюю продолжительность пребывания заявки в системе.
Решение
Каждая бригада в мастерской рассматривается как КО, следовательно, ремонтная мастерская представляется в виде 3-канальной СМО.
1. Определим интенсивность потока обслуживания
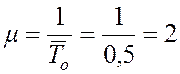 ;
;
2. Приведенная интенсивность потока заявок
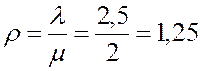 ;
; 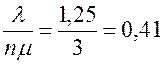 - коэффициент загрузки КО
- коэффициент загрузки КО
Поскольку 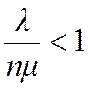 , то очередь не растет безгранично и в системе наступает предельный стационарный режим работы.
, то очередь не растет безгранично и в системе наступает предельный стационарный режим работы.
3. Вычислим вероятности состояний системы:
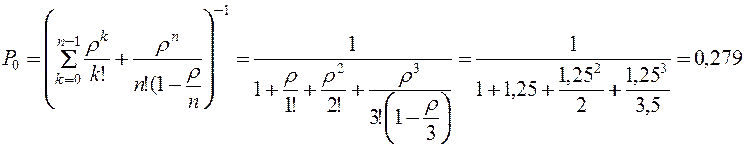 .
.
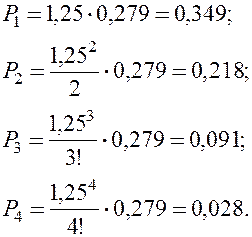
4. Вероятность отсутствия очереди у мастерской
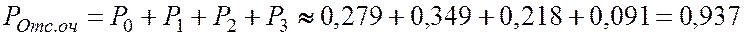 .
.
5. Среднее число заявок в очереди на обслуживание
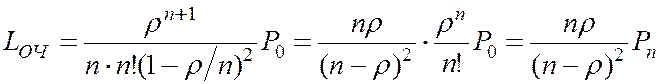 .
.
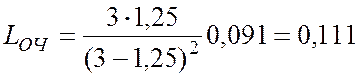 .
.
6. Среднее число находящихся в системе заявок
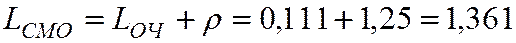 .
.
7. Средняя продолжительность пребывания заявки в очереди на обслуживание
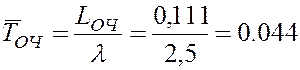 суток.
суток.
8. Средняя продолжительность пребывания механизмов в мастерской (в системе)
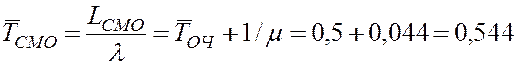 суток.
суток.
Задача 2. Система массового обслуживания - билетная касса с тремя окошками (с тремя кассирами) и неограниченной очередью. Пассажиров, желающих купить билет, приходит в среднем 5 человек за 20 мин. Поток пассажиров можно считать простейшим. Кассир в среднем обслуживает трех пассажиров за 10 минут. Время обслуживания подчинено показательному закону распределения. Определите вероятностные характеристики СМО в стационарном режиме. Составьте процедуру статистического моделирования работы СМО и проведите испытания.
Многоканальная система массового обслуживания с ожиданием
Входящий и выходящий потоки являются пуассоновскими с интенсивностями 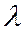 и
и 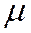 соответственно. Система имеет
соответственно. Система имеет 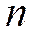 каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна -
каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна - 
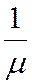 .
.
|
|
|
Очередь ограничена m заявками. Новая заявка, поступающая в момент, когда все места в очереди заняты, покидает СМО необслуженной, т.е. получает отказ.
В установившемся режиме функционирование многоканальной СМО с ожиданием может быть описано с помощью системы алгебраических уравнений:
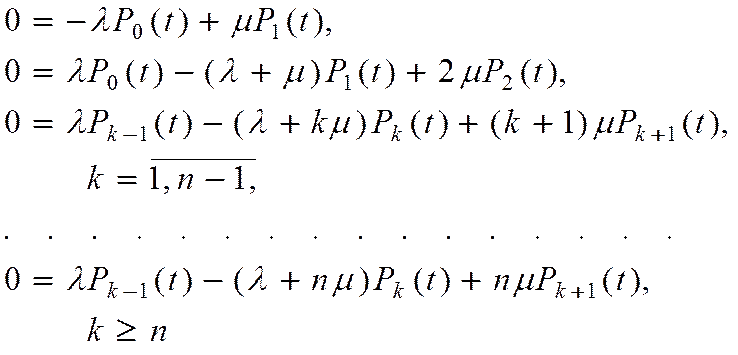
(1)
Решение системы уравнений (1) имеет вид
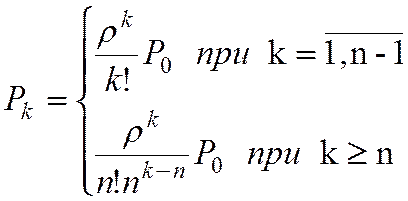 (2)
(2)
где
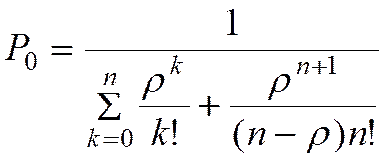
Решение будет действительным, если выполняется следующее условие:
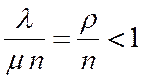 . (3)
. (3)
Характеристики функционирования в стационарном режиме многоканальной СМО с ожиданием определяются по следующим формулам:
- среднее число заявок в очереди на обслуживание
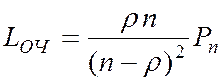 (4)
(4)
- среднее число находящихся в системе заявок
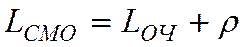 (5)
(5)
- средняя продолжительность пребывания заявки в очереди
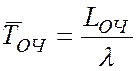 (6)
(6)
- средняя продолжительность пребывания заявки в системе
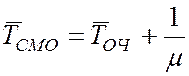 (7)
(7)
|
|
|


