 |
Выделение локальных областей
|
|
|
|
Допустим, что нам предстоит оптимизировать смесь для производства силикатного кирпича, состоящую из нескольких компонентов – извести, песка и воды. Если за основу взять симплекс третьего порядка (рисунок 2), то становится самоочевидно, что проведение эксперимента в первой, четвертой и седьмой точках решетки практически исключается, так как смеси, содержащие только индивидуальные компоненты, для достижения цели совершенно непригодны.
В этих случаях исследования нужно проводить в локальных областях факторного пространства, т. е. внутри внешнего симплекса надо выделять внутренний. Естественно, что две системы координат внутреннего и внешнего симплексов должны быть согласованы между собой. Для выделения внутренних локальных областей в факторном пространстве должны быть заданы координаты вершин многоугольников, причем точки могут располагаться как угодно, в любом месте. Их положение фиксируется с помощью матриц. Элементами каждой строки являются координаты одной точки (вершины) внутреннего симплекса в единицах внешнего симплекса.
При выделении локальной области следует придерживаться основных правил:
• точка (А) может располагаться в любом месте внешнего факторного треугольника;
• точка (В) должна быть вершинной точкой треугольника ABC и не может располагаться ниже точки (А);
• точка (С) должна располагаться правее точки (А);
• обегание вершин в треугольнике ABC должно осуществляться по часовой стрелке: (А) => (В) => (С);
• точка (D) в четырехкомпонентном симплексе должна занимать самое верхнее положение (координата Z4 точки D должна быть максимальна).
Для перевода координат относительных единиц внутреннего симплекса в натуральные единицы внешнего симплекса следует использовать следующие формулы:
|
|
|
а) для трехкомпонентного симплекса
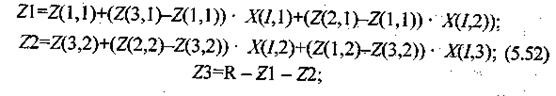 |
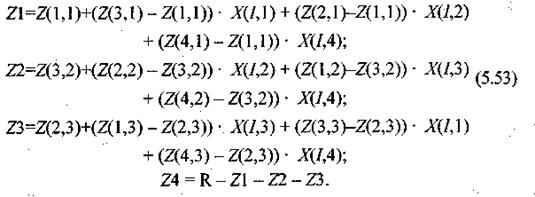 |
для четырехкомпонентного симплека
51. Методы многомерного поиска. Покоординатный спуск. Методы многомерного поиска. (в случае, когда F- функция более чем одного фактора).
Рассмотрим в простейшем варианте, когда оптимизация проводится без ограничений. Ограничения вносят заметные усложнения в алгоритмы поиска, но при этом их сущность не изменяется. Изложение будем иллюстрировать случаем двух факторов. Рассматривается поиск мах.
Покоординатный спуск. Этот метод сводится к следующему.Выбираются координаты начальной точки поиска х1u и х2u, т. е. те значения х1 и х2 от которых мы начнем искать оптимум. Выбираются единичные приращения факторов (шаги) Н1 и Н2, а так же малые приращения факторов ε1 и ε2. Выбор всех этих величин определяется физическим смыслом задачи и той информацией о ней, которой мы располагаем заранее.
Рассчитывается значение F(х1u; х2u) в точке 1(рис 1). Далее не меняя величины х2, начинаем двигать вдоль оси х1, давая на каждом шаге этому фактору приращение Н1. На каждом шаге – в точках 2,3,4, и т. д. – проводится расчет F. Шаги продолжаются до тех пор, пока продолжается рост F. Неудачными будем считать те шаги, на которых получено меньшее значение F, чем на предыдущих
0- удачные шаги,х- неудачные шаги
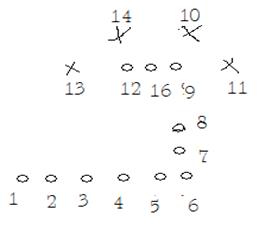 После первого неудачного шага (точка 6) возвращаемся в предыдущую точку (в данном случае в точку 5), фиксируем величину х1 и начинаем изменять х2, давая ему приращения Н3 или Н2 (точки 7,8,9,10).Затем снова движемся вдоль оси х1 (точки 11,12,13), снова меняем направление (точки 14,15) и т. д. (разумеется, если факторов больше двух, то после движения вдоль осей х1 и х2 проводится движение вдоль осей х3 и х4 и лишь затем движемся вдоль оси х1.На рис 1 изображена ситуация, когда из точки 12 двигаться некуда: во всех окружающих точках (9,13,14,15) значение F меньше, чем в данной. Это значит, что мы уже приблизились к мах и прежние крупные шаги из точки 12 переносят нас через него. Поэтому уменьшаем шаги и продолжают поиск уменьшенными шагами. Уменьшение шага может производиться неоднократно. Но в этот момент, когда уменьшенные шаги оказываются меньше чем, соответственно, ε1 и ε2
После первого неудачного шага (точка 6) возвращаемся в предыдущую точку (в данном случае в точку 5), фиксируем величину х1 и начинаем изменять х2, давая ему приращения Н3 или Н2 (точки 7,8,9,10).Затем снова движемся вдоль оси х1 (точки 11,12,13), снова меняем направление (точки 14,15) и т. д. (разумеется, если факторов больше двух, то после движения вдоль осей х1 и х2 проводится движение вдоль осей х3 и х4 и лишь затем движемся вдоль оси х1.На рис 1 изображена ситуация, когда из точки 12 двигаться некуда: во всех окружающих точках (9,13,14,15) значение F меньше, чем в данной. Это значит, что мы уже приблизились к мах и прежние крупные шаги из точки 12 переносят нас через него. Поэтому уменьшаем шаги и продолжают поиск уменьшенными шагами. Уменьшение шага может производиться неоднократно. Но в этот момент, когда уменьшенные шаги оказываются меньше чем, соответственно, ε1 и ε2
|
|
|
Логично считать, что мах зафиксирован достаточно точно и можно закончить расчет, приняв лучшую точку за оптимум.
|
|
|


