Статистические модели в виде линейных полиномов. Метод наименьших квадратов для линейного уравнения регрессии.

В исследовании объектов ХТ во многих случаях связь между выходными параметрами и факторами можно апроксимировать линейной зависимостью. приступая к исследовании процессов априорных данных о которым недостаточно исследователи начинают с самых простых моделей процесса.

Линейный полином: y⁼=b₀+b₁*x_i

Чтобы найти значения коэффициентов b₀и b₁ следует провести не менее 2 опытов и решить уравнения.

У₁= b₀+b₁*x_iI;y=b₀+b₁*x₁₂

Если исследовании система хар-ется линейной зависимостью и в ней не возникают помехи,тогда все экспериментные данные должны укрепляться на влиянием случайных факторов. Тогда для нахождения b₀ и b₁ наблюдается Nопытов и получают переопределенную систему уравнений:

Y₂=b₀+b₁*x₁₂

Y₁=b₀+b₁*x₁₁

Y_N=b₀+b₁*x_1N

В таком случае возникает задача усреднения данных. самым распространенным,хотя и не единственным способом усреднения данных является метод наименьших квадратов-суммы квадратов отклонений выходного параметра должны быть минимальны.

F= 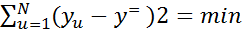или с учетом y⁼=b₀+b₁*x₁F= 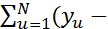b₀-b₁*x_iu)² = min. Т.е. наилучшие будут те значения параметров, в которых сумма квадратов отклон. расчетных величин от эксперимент. окажется наименьшей. Преимущества метода наим. квадратов: 1.простота вычисляемых операций. 2. высокая точность результатов.

Т.о. процедура нахождения коэффициентов уравнения регрессии сводится к задаче определить min функции необходимым условием minфункции нескольких переменных является выполнение условий равенства.

34. Виды моделей при планировании эксперимента по методике Шеффе. Методика расчета коэффициентов аппроксимирующих полиномов. Выделение локальных областей.

Из числа наиболее опробованных планов можно указать два типа симметричных планов: Шеффе и Дрейпера-Лоуренса. Первые для двух- и трехкомпонентных смесей при одинаковом числе параллельных наблюдений в каждой точке плана в случае моделей в виде третьей степени весьма удачны. Они минимизируют случайные ошибки предсказания этими моделями поверхности отклика. Однако точность моделей ухудшается при использовании планов Шеффе выше третьего порядка.

Планы на симплексных решетках, т.е. планы Шеффе, не обладают обычно свойством композиционности, т.е. для перехода к построению более сложной модели исследователю приходится ставить новые опыты, не полностью используя информацию, полученную из предыдущих опытов. Чтобы уменьшить подобные потери, либо выбирают координаты для контрольных точек в точках плана модели более высокого порядка, либо сразу строят план модели более высокого порядка (n₂>n₁). В многокомпонентных сплавах приходится строить полиномы сравнительно высоких степеней. Условие нормировки 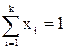облегчает эту задачу, позволяет вместо полных многочленов вида

y=b₀+

использовать либо канонические полиномы Шеффе:

либо однородные полиномы:

Число экспериментальных точек симплексного плана зависят от числа компонентов изучаемой смеси к и выбранной степени полинома

,

где к – число компонентов в смеси, р – степень полинома

Например для получения модели четвертой степени (р =4) для системы из пяти компонентов (к =5) необходимо провести следующее число опытов (N)

Использование приведенных полиномов позволяетт уменьшить число опытов для аппроксимации свойств и оценки адекватности модели полиномами одного и того же порядка.

Виды моделей и расчет коэффициентов. Коэффициенты аппроксимирующих полиномов представляют собой комбинации значений изучаемого свойства, полученных в узлах симплексных решеток для S-компонентных смесей n-го порядка.

Например, в модели второго порядка для трехкомпонентной смеси:

 

 

 

 

Модель второго порядка для S-компонентной смеси:

 

 

Чтобы воспользоваться формулами вычисления коэффициентов моделей следует оговорить расположение экспериментальных точек, значения показателя в которых подставляются в эти формулы.

В каждой узловой точке симплекса третьего порядка содержится по три части компонентов.

В первой точке смесь состоит из трех частей третьего компонента; в шестой точке к одной части первого компонента добавлено две части второго; в восьмой – к двум частям второго добавлена одна часть третьего, а десятая точка содержит по одной части всех трех компонентов.

 

 

Рисунок 1 – Барицентрическая система Рисунок 2 – { S, n}-решетка

координат Шеффе { S, n} = {3, 3}

 

Чтобы ставить эксперимент на решетке трехкомпонентного симплекса четвертого порядка, следует иметь в виду, что смеси во всех узловых точках в этом случае состоят уже из четырех частей. Так, например, в четвертой точке содержится три части первого и одна часть третьего компонента и т. д.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: