Главная | Обратная связь | Поможем написать вашу работу!

Математическое моделирование гидродинамической структуры однофазных потоков. Типовые модели.

Любой химико-технологический процесс,какправило,сопровождается перемещением материальных потоков жидкости или сыпучих материалов.Потоки могут быть однофазными,т.е. состоять целиком из одной фазы перемещаемой в аппарате и многофазной (в частности 2-х фазной),когда процесс происходит в условиях взаимодействия нескольких фаз(г-ж,ж-тв,г-тв)

Гидродинамика реальных потоков настолько сложна,что возможно составть в общем виде лишь ур-е для однофазных потоков(ур-е Новье-Стокса)

Однако,решение этих ур-й можно найти лишь для частных случаев.Для многофазных потоков ур-е не получены даже в общем виде.Поэтому,при разработке модели принимают упрощающие допущения.

Структура движущейся технологической среды хар-ся степенью перемешивания частиц потока,который определяет поле концентрации и градиент температуры,это послужило предпосылкой для установления типовых моделей движущихся потоков.Прежде всего это 2 типовые модели:

1. Модель идеального перемешивания(смешения)МИС

2. Модель идеального вытеснения(МИВ)

Указанные модели соответствуют идеальным потокам,однако их можно использовать и для характеристики реальных потоков.Кроме того к типовым моделям гидродинамических потоков относят:

· Ячеячную

· Диффузионную

· Комбинированную

Модели, которые характеризуют реальные потоки. Эти модели в придельных условиях переходят в модель идеального вытеснения или в модель идеального смешения.Модели структуры потока записываются в виде диф. Ур-й,которые выражают связь между наиболее характерными параметрами процесса.

Универсальным видом гидродинамической модели является ур-е характеризующее изменение концентрации в-ва в потоке,которое обуславливается только движением.При этом принимаетcя допущение,что скорость хим.реакцииравно 0.

При построении модели структуры потока следует учитывать,что модель должна

1)отражать физическую сущность реального потока и в тоже время иметь сравнительно простое математическое описание.

2)давать возможность определить ее параметры(коэффициент уравнений)экспериментальным или ресчетным способом.

3)должна быть удобной для использования при расчетах конкретных ХТП.

Метод наименьших квадратов. Постановка задачи и общий вид решения. Система нормальных уравнений

Метод наименьших квадратов-суммы квадратов отклонений выходного параметра объекта и модели должны быть минимальным

Или с учетом ур-я: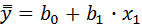

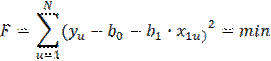
Т.е. наилучшими будут те значения параметров bпри кот. Сумма квадратов отклонений расчетных величин от экспериментальных окажется наименьшей

Достоинства этого метода

· Простота вычислительных операций

· Высокая точность результатов(при достаточном объеме данных)

Т.о. процедура нахождения коэф. Ур-я регрессии сводится к задаче определения min ф-ции

Необходим условием min ф-ции нескольких переменных является выполнение условия равенства нулю частных производных по искомым величинам(коэффициентом полинома)