Критерии проверки статистических гипотез. Проверка однородности дисперсий.

Обычная процедура проверки гипотез заключается в следующем:

1) по выборочным данным рассчитывается критерий проверки;

2) полученное значение критерия сравнивают с критическим значением, находимым из таблиц. Критическое значение каждого конкретного критерия определяется уровнем значимости и числом степеней свободы, по которому были рассчитаны величины, входящие в критерий.

Рассмотрим некоторые часто встречающиеся критерии проверки гипотез.

Критерий исключения грубой ошибки. Если результаты эксперимента получены из-за грубой ошибки, то их необходимо отбросить, не подвергая никаким статистическим оценкам. Необходимо произвести проверку резко выделяющихся значений.

Критерий проверки имеет вид

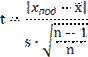
где x_под – «подозрительный» результат (наибольший или наименьший);

– среднее, полученное по формуле;

S – среднеквадратичное отклонение; при этом в расчет х и S включается «подозрительный» результат;

n – количество измерений.

Полученное значение критерия сравнивают с табличным. Также можно использовать, критерий Ирвина λ, который основан на разности x_n и x_n+1 (двух наибольших значений СВ):

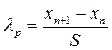
Если полученное значение λ_p больше значения, соответствующего табличному λ_кр то его следует оставить.

Критерий Пирсона χ². Для проверки гипотезы о соответствии эмпирического распределения СВ теоретическому наиболее часто применяют критерий Пирсонаχ²

Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что СВd имеет данный закон распределения заданный функцией F(d) или плотностью вероятности f(d). Назовем этот закон распределения «теоретическим».

Зная этот закон, можно вычислить ожидаемое число отказов изделия в определенных интервалах, на которые разбить время испытания.

В результате получим теоретический ряд частот в k интервалах времени испытаний:

Подсчитаем также число отказавших изделий в этих же интервалах в нашем опыте и получим экспериментальный ряд частот

Для проверки согласованности теоретического и экспериментального распределений подсчитывается мера расхождения χ².

и число степеней свободы v=k–f, где f – число ограничений. Число ограничений равно числу параметров распределения, увеличенному на единицу. Для распределения Пирсона составлены специальные таблицы.

Критерий Колмогорова λ. Критерий Пирсона применяют только в тех случаях, когда число наблюдений (n≥25). Если теоретические значения параметров распределения известны, то лучшим критерием является критерий Колмогорова.

Составляют разность между накопленными теоретическими и эмпирическими суммами и находят максимальное значение этой разности, вычисляя величину D по формуле:

Где , – разность функций экспериментального и теоретического распределения СВ.

Коэффициент λ находят по формуле:

Пользуясь табличными данными для вычисленного значения λ, определяют вероятность P(λ) – вероятность того, что гипотетическая функция выбрана правильно.

Критерий Фишера F. Прежде чем сравнивать средние значения двух выборок, необходимо убедиться в равенстве их дисперсий. При нормальном законе распределения СВ для проверки гипотезы о равенстве (однородности) выборочных дисперсий в качестве критерия используется статистика, которая равна отношению двух независимых оценок дисперсий генеральной совокупности и , имеющих степень свободы соответственно v₁ и v₂, т.е.

При этом должно выполняться услови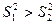е , где – большая величина выборочной дисперсии в двух выборках.

Найденное значение сравнивается стабличным при заданном уровне значимости p и степенях свободы v₁=n₁–1 и v₂=n₂-1. Если F<F_кр, тогда гипотеза о равенстве выборочных дисперсий принимается.

Критерий КохренаG. Если число параллельных опытов в сериях одинаково, то однородность дисперсий нескольких выборок проверяется с помощью критерия КохренаG по формуле:

где – максимальная дисперсия, а – сумма всех дисперсий выборок, N – число выборок, n – номер выборки.

Если расчетное значение G больше табличного G_кр (при уровне значимости α и степенях свободы v₁=n₁–1 для числителя и v₂=N для знаменателя), то гипотеза о равенстве (однородности) дисперсий отвергается.

Если проверка по критериям Фишера и Кохрена покажет, что для оценок дисперсий можно принять нуль-гипотезу, оценки называют однородными; эту процедуру часто называют проверкой однородности дисперсий. Однородные оценки можно усреднить – найти единую оценку дисперсии по всей совокупности измерений; для этого пользуются формулой:

Критерий Стьюдента t. Для проверки гипотезы о равенстве двух выборочных средних значений СВ, имеющей нормальный закон распределения, используют критерий Стьюдента t.

Нуль-гипотеза здесь: средние значения в двух сериях измерений являются оценками одного и того же генерального значения (математического ожидания, истинного значения).

Если серии измерений, в которых получены средние, сделаны с разной точностью (с разными дисперсиями), то процедура сравнения средних резко усложняется. В этих случаях можно рекомендовать специальные методы. Если дисперсии однородны и найдена общая оценка, тогда проверка проводится по критерию Стьюдента

где п₁ и n₂ – числа измерений в первой и второй сериях; s – единая оценка стандартного отклонения по всей совокупности измерений.

Критическое значение t зависит от v и α.