Процессы транспортирования пищевых материалов

В процессе проектирования новых технических систем пищевых производств приходится рассматривать большой круг задач механики, в том числе не только с механическими процессами обработки пищевого сырья и полуфабрикатов, но и с процессами транспортирования пищевых сред.

Транспортирование пищевых материалов может происходить при различных условиях, например, в свободном потоке в рабочих зонах машин, различных каналах и трубопроводах или путем медленного перемещения больших масс в накопителях, бункерах, силосах и т.п. под воздействием различных внешних сил, изменяющихся по определенным закономерностям.

При решении этих задач используются известные уравнения теории свободного движения тела, а в соответствующих случаях соотношения механики сплошных сред.

Известные дифференциальные уравнения движения центра тяжести свободной частицы постоянной массы в прямоугольной системе координат в случае неподвижной среды имеют вид [32]

,

где 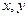- координаты точек траектории движения, 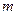- масса движущейся частицы; 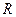- сила сопротивления среды; - сила тяжести; - угол наклона к горизонту касательной к траектории движения.

Из данных уравнений вытекают следующие свойства элементов траектории движения частицы:

- если угол , то скорость движения ни в одной точке траектории не равна нулю,

- угол наклона касательной к траектории уменьшается по мере движения частицы вдоль траектории,

- горизонтальная скорость движения частицы убывает по мере продвижения ее вдоль траектории,

- кривизна траектории (рис.2.49) равна ,

 

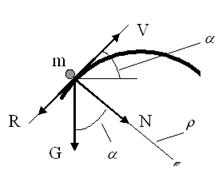
Рис.2.49 Силы, действующие на частицу на участке траектории с кривизной

- для одной и той же ординаты на восходящем и нисходящем участках траектории ее элементы связаны следующими неравенствами , .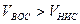

Сопротивление среды движению частицы можно рассматривать как функцию от скорости ее движения . Если кривая изменения скорости в зависимости от сопротивления среды не имеет перегибов, т.е. если ни на одном из участков, то закон изменения сопротивления среды от скорости будет монотонным.

По Ньютону сопротивление среды движению тела подчиняется квадратичному закону , где 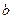- коэффициент, характеризующий свойства среды и тела.

Любой закон сопротивления среды в определенном диапазоне изменения скоростей можно заменить линейным законом (рис.2.50), условия применимости которого при определении элементов траектории записывается в виде , где - численные значения рассматриваемого элемента (скорости, времени, длины дуги траектории и пр.) при действительном и линейном законах сопротивления среды, - допускаемый процент ошибки.

Рис. 2.50 Аппроксимация квадратичного закона сопротивления среды линейным законом

 

¨ Условия движения частицы при линейном законе сопротивления среды

Из решения дифференциального уравнения при и начальных условиях 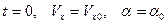следует 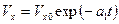, где .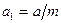

Абсцисса траектории .

Ордината траектории , где .

 

¨ Условия движения частицы при квадратичном законе сопротивления среды

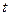При квадратичном законе сопротивления среды (при аргументе ) из решения уравнения , где при начальных условиях следует, что , где .

.

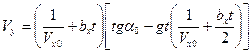Длина дуги траектории .

 

 

¨ Анализ движения частицы при боковом направлении воздушного потока

В некоторых технологических процессах, например, процессах разделения частиц на фракции, может иметь место свободное движение частиц в движущемся воздушном потоке.

Рассмотрим задачу движения частицы при боковом движении воздушного потока при допущении, что скорость этого потока будет постоянной на всей траектории движения частицы.

Полная скорость движения частицы будет равна или .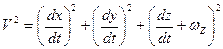

Дифференциальные уравнения движения

.

Разделив почленно первое и третье уравнения, получим , решение которого дает значение искомой величины .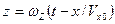

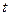С помощью этой формулы можно определить отклонение траектории движения частицы в случае бокового направления воздушного потока при . Можно видеть, что при боковом направлении воздушного потока боковое отклонение частицы зависит от скорости потока , сносящего частицу, абсциссы траектории , горизонтальной компоненты начальной скорости частицы и времени движения . Влияние аэродинамических свойств среды и частицы на величину ее отклонения косвенно учитывается величиной .

Анализ движения частиц материала по трубопроводу. Рассмотрим условия движения частицы твердого материала по трубопроводу прямоугольного сечения, нижняя плоскость которого установлена под наклоном к линии горизонта (рис.2.51).

Рис.2.51 Схема участка трубопровода

Будем считать, что масса транспортируемых по трубопроводу частиц, проходящая в единицу времени через любое сечение трубопровода равна , где - скорость воздушного потока в трубопроводе, - плотность потока частиц.

На отдельную частицу массой действуют сила тяжести 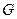, сила сопротивления среды 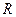, направленная под углом к оси 0Y, сила трения и сила реакции (рис. 2.52)

Рис.2.52 Схема сил, действующих на частицу материала

 

Уравнение движения частицы в проекциях на оси 0Х и 0Y:

где , -аэродинамические коэффициенты, 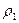- плотность воздушного потока, 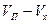- относительная скорость движения потока и частицы, - площадь миделевого сечения частицы и ее поверхности соответственно.

Предельная скорость частиц будет равна ,

где и .

Процессы транспортирования сыпучих материалов реализуются в пневмосистемах крупных хлебокомбинатов (рис.2.53).

а) б)

 

Рис. 2.53 Схема пневмосистемы транспортирования муки (а) и побудитель тяги (б)

 

¨ Распределение сыпучих материалов по емкостям

Для распределения смеси сыпучих материалов по емкостям, перемещаемой воздушным потоком по трубопроводу, используются широко известные двухпозиционные распределители, которые представляют собой управляемую заслонку (клапан), перекрывающий центральный трубопровод или отвод к данной емкости. Эти устройства просты по конструкции и высоко надежны, однако их использование оправдано, если число емкостей не более двух. При большем числе емкостей перед каждой необходимо устанавливать такой распределитель, что усложняет управление системой транспортирования и распределения сыпучих материалов по емкостям, делает ее громоздкой, энерго- и металлоемкой.

Более эффективной конструкцией распределителя является мехатронное многопозиционное устройство распределения сыпучих материалов, позволяющее обслуживать от 2 до 12 емкостей по их запросам или по обегающей системе [44]. Это устройство содержит мальтийский крест, число позиций которого равно числу обслуживаемых емкостей, соединенных с ним трубопроводами. Сигнал датчика уровня емкости заставляет срабатывать привод поводка мальтийского механизма, и патрубок центрального трубопровода позиционируется мальтийским крестом относительно трубопровода обслуживаемой емкости (рис.2.54)

Рис. 2.54 Схема многопозиционного устройства распределения сыпучих материалов по емкостям

5, 15 – трубопроводы к емкостям, 6 – центральный трубопровод, 7 – основание мальтийского креста, 8 – платформа, 9 – редуктор, 10 – поводок, 11 – ролик поводка, 12 – мальтийский крест, 13 – втулка, 14 – патрубок, 16 – кронштейн, 17 – пружина, 18 – электродвигатель, 19 – датчик положения, 20 - эжектор

 

¨ Анализ движения материала в вертикальном бункере

Рассмотрим процесс движения массы материала, состоящего из отдельных частиц, в вертикальном бункере, которые подаются в него по трубопроводу с помощью воздушного потока (рис.2.55).

Материал, подаваемый в бункер, обладает упругими свойствами, и в процессе заполнения бункера возникают боковые и осевые усилия. Величину давления на стенки бункера можно принять как часть осевого давления столба материала в бункере , где - боковое давление материала, - осевое давление материала, 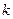- коэффициент пропорциональности.

Рис.2.55 Схема действующих сил на материал в бункере

 

Определим зависимость, характеризующую изменение осевого давления по высоте бункера накопителя, в предположении, что нормальные напряжения в любой точке сечения материала перпендикулярного оси одинаковы и давление воздушного потока равномерно распределяется по плоскости сечения бункера.

Выделим на расстоянии от начала координат элементарный слой материала толщиной 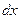. Площадь сечения бункера , где 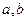- размеры сечения бункера. Выделенный элемент представляет собой параллелепипед с основаниями равными и боковыми гранями и . На выделенный элемент оказывают действие следующие силы:

- сила давления воздушного потока , где - плотность воздушного потока, -аэродинамический коэффициент, 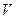- скорость воздушного потока,

- сила реакции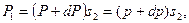

- силы нормального давления

- силы трения материала о стенки

- сила тяжести , где - объем элемента, .

Уравнение равновесия относительно оси

Разделив переменные и решив уравнение, получим .

При 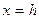давление будет равно , где - высота бункера накопителя, , - объемная масса материала в бункере.

Условные обозначения

- момент инерции рабочего органа измельчителя

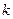- коэффициент восстановления материала после ударного воздействия рабочего органа измельчителя

- импульс ударного воздействия

- полная работа внешних сил при дроблении материала

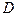- степень дисперсности материала при измельчении

- производительность (пропускная способность) машины или аппарата

- плотность материала

- угловая частота вращения

- установленная мощность двигателя привода

- фактор разделения материала при протирании

- сила воздушного сопротивления при движении частицы

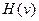- полнота смешивания

- коэффициент смешивания

- дисперсия фактической доли компонента в пробе смеси объема единиц

- энтропия смеси

- коэффициент однородности смеси

- порог связности частиц из одного вида материала в смеси компонентов

- средний диаметр жировых шариков при гомогенизации молока

- расходно-напорная характеристика формующей части экструдера

- расходно-напорная характеристика нагнетающей части экструдера

- скорость бокового движения частицы при ее транспортировании

- осевое давление материала в бункере

- боковое давление материала в бункере

- нормальное напряжение

- касательное напряжение

- модуль упругости

- деформация растяжения

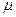- вязкость материала

 

Глоссарий

Измельчение – механический процесс образования новых поверхностей частиц материала путем их дробления

Диспергирование – процесс измельчения частиц до коллоидной степени дисперсности

Протирание – механический процесс отделения массы сырья путем его продавливания через сито

Финиширование – процесс тонкого измельчения протертой массы продавливанием через сито с небольшими отверстиями

Гомогенизация – процесс измельчения жидких и пюреобразных продуктов при их пропускании под давлением через узкие щели

Грубодисперсные системы – системы с частицами дисперсной фазы менее 10^-3 см

Микрогетерогенные системы - системы с частицами дисперсной фазы 10^-3 …10^-5 см

Ультрамикрогетерогенные системы - системы с частицами дисперсной фазы 10^-5 …10^-7 см

Дисперсионная среда – сплошная часть неоднородных дисперсных систем

Дисперсная фаза – входящая в качестве содержимого в дисперсную систему

Конденсация – укрупнение частиц до коллоидной степени дисперсности

Сортирование – механический процесс разделения сыпучих материалов на фракции, различающиеся качеством частиц

Калибрование - механический процесс разделения сыпучих материалов на фракции, различающиеся величиной частиц

Проход – часть сыпучего материала, прошедшая через отверстия сита при сортировании

Сход – часть сыпучего материала, не прошедшая через отверстия сита при сортировании

Самосортирование – процесс перемещения частиц с меньшими размерами и коэффициентом трения из верхних слоев в нижние

Смешивание – механический процесс, заключающийся в обеспечении равномерного распределения компонентов смеси в общем ее объеме в соответствии с заданным долевым участием компонентов

Конвективное смешивание – процесс перемещения групп частиц из одного объема смеси в другой внедрением и скольжением слоев

Диффузионное смешивание – процесс перемещения частиц различных компонентов через вновь образуемые границы их раздела

Сегрегация – группирование близких по форме и размерам частиц в разных местах смесителя

Связность частиц – контактирование соседних частиц из одного вида материала друг с другом

Слоистость частиц – контактирование частиц из одного вида материала друг с другом по горизонтали

Струйность частиц - контактирование частиц из одного вида материала друг с другом по вертикали

Показатель полноты смешивания – отношение отклонения реального состава смеси от заданного в разных объемах смеси

Денатурация – негидролитическое изменение нативной (первоначальной) структуры белка вследствие механического, химического или теплового воздействия

Синерезис – самопроизвольный процесс разделения продукта на две фазы, сопровождаемый изменением его объема

Коагуляция – процесс взаимофиксации выведенных из состояния агрегативной устойчивости частиц дисперсной фазы, проявляющийся в самоукрупнении коллоидных частиц

Предел текучести – предел напряжения сдвига, при котором возникает течение материала

Ньютонова жидкость - жидкие продукты, у которых коэффициент вязкости есть постоянная величина, т.е. когда скорость деформации жидкой среды пропорциональна напряжениям сдвига.

Плотность продукта – характеристика физико-механических свойств продукта, равная отношению его массы к единице объема

Прочность продукта – способность сопротивления материала противодействовать механическому разрушению

Упругость продукта – способность материала мгновенно восстанавливать свою форму после снятия внешней нагрузки

Эластичность – способность продукта восстанавливать форму через некоторый промежуток времени после снятия нагрузки

Пластичность – свойство продукта, характеризуемое получением необратимой деформации при определенной величине нагрузки

Релаксация – свойство продукта, характеризующее время перехода упругой деформации в пластическую при постоянной нагрузке

Вязкость – характеристика внутреннего трения, возникающего при относительном движении слоев жидких продуктов

Адгезия – способность проявления связей продукта с рабочим органом, тарой или с другим продуктом.

 

Контрольные вопросы

1.Какие существуют механические способы измельчения материалов?

2.По каким признакам классифицируют продукты по степени измельчения?

3.Что понимается под степенью измельчения?

4.На что затрачивается работа при измельчении материала?

5.Какова сущность ударного способа измельчения твердых материалов?

6.Каково устройство молотковой дробилки?

7.От каких параметров зависит производительность молотковой дробилки и степень измельчения продукта?

8.Какой процесс называется протиранием?

9.Как классифицируется протирочное оборудование?

10.Какие требования предъявляются к протирочным машинам?

11. Что понимается под процессом гомогенизации?

12.От каких факторов зависит степень гомогенизации?

12.Каково устройство и принцип действия клапанного гомогенизатора?

13.Каковы задачи сортирования материалов?

14.В чем заключается основное условие просеивания частиц?

15.Какими показателями оценивается качество смешивания сыпучих компонентов?

16.Что происходит при конвективном и диффузионном смешивании частиц?

17.Что понимается под связностью частиц при смешивании, и какие виды связности существуют?

18.Какие явления происходят при транспортировании частиц по продуктопроводам?

19. Какие параметры характеризуют движение сыпучих частиц в бункерах?

20. В чем сущность перемешивания пластичных и вязкоупругих пищевых сред, и на каком оборудовании осуществляется процесс перемешивания?

21.Какие явления происходят при раскатывании теста?

22. Какими показателями характеризуются физико-механические свойства пищевых материалов?

23.Какими основными реологическими свойствами обладают пищевые материалы, проявляемыми при их механической обработке?

 

 

3.Гидромеханические процессы. Основные понятия и закономерности

 

3.1.Основные понятия гидростатики и гидродинамики

3.2.Понятие о вязкости и течении жидкостей

3.3.Основные факторы гидродинамики аппаратов

Условные обозначения

Глоссарий

Контрольные вопросы

 

Основные понятия гидростатики и гидродинамики

Рассмотрение гидромеханических процессов начнем с основных понятий и закономерностей гидростатики и гидродинамики.

Основное свойство, которое отличает жидкость от твердого тела, заключается в том, что жидкость не способна сдерживать ни на одно мгновение напряжения сдвига. Если к жидкости приложить напряжение сдвига, то она начнет течь. Одни жидкости текут медленно, например, мед, другие, как вода и некоторые масла, быстро. Мерой легкости, с которой жидкость течет, является ее вязкость.

Гидростатика – это теория неподвижных жидкостей [23]. Если жидкость находится в покое, то на нее не действуют никакие сдвиговые силы. Поэтому закон гидростатики заключается в том, что напряжения внутри жидкости всегда нормальны к любой ее поверхности.

Нормальная сила на единицу площади называется давлением. Ясно, что если в неподвижной жидкости нет сдвигов, то напряжение давления во всех направлениях одинаково (рис. 3.1).

Рис. 3.1. Давление в неподвижной жидкости

Если плотность жидкости считать постоянной и обозначить давление на некотором нулевом уровне через , то давление на высоте , будет равно 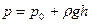. Соотношение для неподвижной жидкости.

Условно выделим в жидкости маленький кубик со сторонами 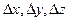и определим действующую на него силу

Рис. 3.2. Сила давления, действующая на элементарный кубик

Так как давление в любом месте во всех направлениях одинаково, то полная сила, действующая на единичный объем, может быть обусловлена только изменением давления. Пусть давление меняется в направлении оси . Давление на грань с координатой дает силу , а давление на грань с координатой дает силу . Результирующая сила равна .

Если учесть остальные грани, то сила давления на единичный объем равна . При наличии других сил, например, сил тяжести, давление при равновесии должно компенсироваться ими.

Дополнительные силы можно описать потенциальной энергией. Обозначим через 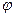потенциальную энергию единицы массы (для притяжения ). Сила, действующая на единичную массу, задается через потенциал 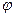выражением , и если учесть плотность жидкости , то на единицу объема будет действовать сила .

В состоянии равновесия эта сила вместе с силой давления должны быть равны нулю - это и есть уравнение гидростатики.

Если плотность изменяется в пространстве, то нет возможности уравновесить все силы, и жидкость не может находиться в состоянии статического равновесия – в ней возникнут конвекционные потоки. При постоянной плотности решение уравнения имеет вид .

Чтобы описать движение жидкости необходимо задать в каждой точке некоторые ее свойства. Так, если жидкость движется в разных местах с различными скоростями, то, чтобы определить характер потока в каждой точке и в любой момент времени, нужно задать три компоненты скорости. Причем скорость не является единственной характеристикой жидкости: от точки к точке может меняться плотность, температура, давление.

Уравнение состояния жидкости, связывающее давление и плотность

.

Уравнение непрерывности выражает сохранение массы жидкости. Если вещество вытекает из какой-то точки, то его количество в этой точке должно уменьшаться. Если скорость жидкости равна , то масса, которая протекает за единичное время через единицу площади поверхности, равна нормальной к поверхности компоненте . Дивергенция такой величины определяется скоростью уменьшения плотности.

.

При несжимаемой жидкости плотность ее постоянна и уравнение непрерывности записывается как .

Следующее уравнение гидродинамики получается из уравнения Ньютона. Произведение массы элемента жидкости на ускорение должно быть равно силам, действующим на этот элемент:

, где - сила, действующая на единичный объем.

Плотность сил можно записать в виде трех слагаемых: силы давления на единицу объема ; консервативных сил, приводящей к плотности сил ; внешней силы, приходящейся на единицу объема .

Уравнение движения .

Рассмотрим изменение скорости капельки жидкости. За небольшой интервал времени эта капелька изменит свое положение и в направлении оси передвинется на расстояние , аналогичные перемещения произойдут и в направлении осей и .

Если скорость капельки в момент 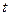, то скорость той же частицы в момент будет 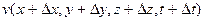, причем и .

Из определения частных производных получим

.

Считая вектором, можно записать и уравнение движения жидкости (без учета силы вязкости) выразится как

.

Под стационарным потоком жидкости понимается поток, скорость которого в любом месте жидкости никогда не меняется. Картина скоростей в таком потоке всегда выглядит одинаково и представляет статическое векторное поле. Для стационарного потока можно записать , т.е. все перемещения в стационарном потоке направлены вдоль линий тока и величина в скобках представляет собой уравнение Бернулли означающее сохранение энергии и позволяющее сразу описать поток.

Пример: Из отверстия, расположенного около дна цилиндрического резервуара вытекает вода. Рассмотрим случай, когда скорость потока в отверстии значительно больше скорости потока вблизи поверхности воды в резервуаре. Давление на поверхность воды равно атмосферному давлению . Такое же давление будет и на бока вытекающей струи. В верхней части резервуара скорость воды примем равной нулю . Гравитационный потенциал на поверхности будет также равным нулю, , а в отверстии . Напишем уравнение Бернулли . Откуда .

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: