 |
Течение жидкостей. Вязкость
|
|
|
|
Рассмотрим реальное поведение жидкости. Из предыдущего материала следует, что законы движения жидкости содержатся в уравнении  . В реальных жидкостях нельзя пренебрегать внутренним трением, называемым вязкостью, как это делается при рассмотрении течения идеальной жидкости.
. В реальных жидкостях нельзя пренебрегать внутренним трением, называемым вязкостью, как это делается при рассмотрении течения идеальной жидкости.
Если приложить к жидкости напряжения сдвига, то, как бы они ни были малы, жидкость «поддается» и течет. В статике, очевидно, никаких напряжений сдвига нет. Вязкость описывает силы сдвига при движении жидкости.
Пусть между двух пластинок находится жидкость и необходимо определить силу сдвига при перемещении верхней пластинки (рис. 3.3), которая движется параллельно с постоянной скоростью  относительно неподвижной нижней пластинки.
относительно неподвижной нижней пластинки.

Рис.3.3 Модель движения жидкости между двумя пластинками
Сила, которая требуется для поддержания движения верхней пластинки, будет пропорциональна площади пластинки и отношению  .
.
Если выделить внутри потока небольшой объем в виде параллелепипеда, то силы в этом объеме определятся как  , где
, где 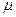 - коэффициент пропорциональности (динамическая вязкость),
- коэффициент пропорциональности (динамическая вязкость),  - площадь верхней грани параллелепипеда,
- площадь верхней грани параллелепипеда,  - скорость изменения деформации сдвига. Тогда можно записать, что
- скорость изменения деформации сдвига. Тогда можно записать, что  . Аналогично соответствующие выражения запишутся для
. Аналогично соответствующие выражения запишутся для  и
и 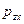 .
.
По характеру поведения различают идеальные, реальные и реологические жидкости. Реологические жидкости характеризуются наличием пластических течений, ползучестью.
В реальных жидкостях при движении возникают силы внутреннего трения, оказывающие сопротивление течению жидкости. Вязкость – это основное отличие реальной жидкости от идеальной. Эталоном для определения вязкости принята дистиллированная вода, с ней сравнивают вязкость других жидкостей. Вязкость, измеряемая в градусах Энглера, определяется отношением времени истечения  200 см3 исследуемой жидкости из специального сосуда ко времени истечения
200 см3 исследуемой жидкости из специального сосуда ко времени истечения 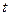 такого же объема дистиллированной воды при температуре 200С,
такого же объема дистиллированной воды при температуре 200С,  .
.
|
|
|
Идеальная жидкость. Если в сплошной среде, которая является мало сжимаемой и находится в покое, выделить некоторый объем и подвергнуть его всестороннему сжатию  , то от давления выделенный объем может изменить только свои размеры, не изменяя первоначальной формы, что будет свидетельствовать об отсутствии касательных напряжений. Величине внешнего давления
, то от давления выделенный объем может изменить только свои размеры, не изменяя первоначальной формы, что будет свидетельствовать об отсутствии касательных напряжений. Величине внешнего давления  внутри выделенного объема будут противостоять только нормальные напряжения, которые нормальны к любой поверхности объема, т.е. давление будет передаваться на все точки объема, и напряжение во всех направлениях будет одинаковым. Данный случай напряженного состояния, поскольку сплошная среда находится в покое, называется гидростатическим давлением.
внутри выделенного объема будут противостоять только нормальные напряжения, которые нормальны к любой поверхности объема, т.е. давление будет передаваться на все точки объема, и напряжение во всех направлениях будет одинаковым. Данный случай напряженного состояния, поскольку сплошная среда находится в покое, называется гидростатическим давлением.
Тензор напряжений в этом случае будет содержать только нормальные компоненты, которые равны между собой  или
или  , причем
, причем  , если
, если  .
.
Если гидростатическое давление не будет менять объема сплошной среды (среда несжимаема) и в ней будет отсутствовать трение, то такая среда будет называться идеальной (паскалевской) жидкостью.
Идеальные жидкости – это несжимаемые жидкости, у которых отсутствует трение.
Уравнение непрерывности  , где
, где  - скорость течения. Стационарное течение идеальной жидкости
- скорость течения. Стационарное течение идеальной жидкости  .
.
Закон сохранения импульса, равный произведению массы на скорость, применим также для вязких жидкостей и турбулентных течений. В объеме жидкости, ограниченной некоторой воображаемой поверхностью, входящий или выходящий через эту поверхность импульс находится в равновесии с внешними силами (давления, напряжения при сдвиге и др.), действующими на поверхность.
Реальные жидкие и полужидкие пищевые продукты являются продуктами с различным реологическим поведением от ньютоновых до зависимых от времени и вязкоупругих.
|
|
|
Ньютоновы жидкости. Если сопротивление движению будет пропорционально относительной скорости перемещения частиц, то жидкости, подчиняющиеся этому закону, называют жидкостями Ньютона-Стокса или ньютоновыми жидкостями. Свойства таких сред описываются линейным уравнением  , где
, где  - касательное напряжение (напряжение сдвига) между двумя соседними слоями,
- касательное напряжение (напряжение сдвига) между двумя соседними слоями,  - скорость сдвига,
- скорость сдвига, 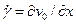 ,
,  - градиент скорости. Напряжение направлено перпендикулярно направлению потока.
- градиент скорости. Напряжение направлено перпендикулярно направлению потока.
При взаимном движении слоев жидкости (деформация сдвига) вязкость  определяет связь между возникающими напряжениями и скоростью деформации.
определяет связь между возникающими напряжениями и скоростью деформации.
Вязкость ньютоновых пищевых сред измеряется в Па·с или г/см·с, текучесть - в см·с/г. Кинематическая вязкость равна отношению динамической вязкости к плотности данной жидкости  , [мм2/с].
, [мм2/с].
Для трехмерного пространства реологическое уравнение состояния ньютоновой жидкости записывается в виде  , где
, где  - компоненты тензора напряжений,
- компоненты тензора напряжений,  - компоненты тензора скоростей деформации.
- компоненты тензора скоростей деформации.
Вязкость жидкостей существенно уменьшается с увеличением температуры. Общей формулы, связывающей вязкость с изменением температуры, не существует. Среди эмпирических формул часто используют формулу Андраде  , где
, где  - постоянные коэффициенты, определяемые опытным путем при изучении конкретных материалов.
- постоянные коэффициенты, определяемые опытным путем при изучении конкретных материалов.
С увеличением давления вязкость жидкостей увеличивается. Изменение вязкости может происходить линейно  или по экспоненте, например, для некоторых растительных масел,
или по экспоненте, например, для некоторых растительных масел,  .
.
Реологическое поведение различных пищевых материалов, отвечающих требованиям ньютоновой жидкости, полностью описывается их вязкостью. К таким продуктам относятся, например, молоко, пиво, вино, чай, кофе, фруктовые нектары, растительные масла, растопленные животные жиры. Однако многие жидкости представляют собой эмульсии или суспензии, в них содержатся водные растворы солей и сахаров, поэтому оценку вязкости таких жидкостей нужно проводить относительно вязкости воды при различных температурах и концентрации.
Например, при оценке вязкости яблочного и других соков и нектаров измерения проводятся на капиллярном вискозиметре в диапазоне температур от 10 до 800С и при различной концентрации сока.
|
|
|
Теория вязкой жидкости, основанная на модели Ньютона, базируется на связи напряжения сдвига между слоями жидкости и скоростями деформации сдвига. Модель вязкой жидкости показывает, что поведение реальных тел может быть различным. Так, пищевые продукты, в зависимости от условий деформации проявляют различные свойства: они могут вести себя как упругие, пластичные тела или истинно вязкие жидкости. Неоднозначное поведение реальных тел необходимо учитывать в комплексе с другими параметрами технологического оборудования при его проектировании.
Если при воздействии неизменной внешней нагрузки, приложенной к телу, смещение частиц тела начинает увеличиваться во времени, то это смещение относят к течению. Течение при очень малых скоростях, когда для перемещения частей тела на 1 мм требуется длительное время, называют ползучестью.
Неньютоновы жидкости. Если напряжения сдвига не пропорциональны скорости сдвига, то такие жидкости относятся к неньютоновым (структурно вязким или аномально текущим). К ним относятся, например, многие лиофильные коллоиды, свойства которых при течении не удается охарактеризовать только одной вязкостью, зависящей не только от температуры и давления, но и от градиента скоростей, продолжительности течения и других факторов.
Эффективная вязкость является функцией от скорости сдвига и времени  .
.
Различают неньютоновскую чисто вязкую жидкость, в которой вся работа внешних сил диссипирует полностью в виде тепла вследствие вязкого трения, и неньютоновскую вязкоупругую жидкость, в которой часть работы идет на упругую обратимую деформацию. Напряжения в общем случае зависят от скорости деформации и от времени, т.е. от величины деформации. Если деформация продолжается достаточно длительное время и при этом устанавливается стационарный режим течения, тогда соотношение между сдвиговыми напряжениями и скоростью деформации представляет кривую течения. Если режим течения не устанавливается, то состояние материала будет непрерывно изменяться во времени.
|
|
|
Неньютоновское поведение жидкостей может проявляться в широком диапазоне скоростей сдвига и напряжений. Для таких сред характерна высокая вязкость в начальный период деформации при небольших напряжениях сдвига, затем последующее значительное падение вязкости, когда напряжение достигнет некоторой предельной величины, называемой пределом текучести  , и маловязкое течение при напряжениях, превышающих данный предел. Твердая дисперсная среда такой структуры начинает разрушаться и течь, когда напряжения превысят предел прочности. Такое реологическое поведение тел называется пластичностью и является характерным для коагуляционных пищевых продуктов с достаточно твердой структурой.
, и маловязкое течение при напряжениях, превышающих данный предел. Твердая дисперсная среда такой структуры начинает разрушаться и течь, когда напряжения превысят предел прочности. Такое реологическое поведение тел называется пластичностью и является характерным для коагуляционных пищевых продуктов с достаточно твердой структурой.
При переходе от низких  к высоким напряжениям
к высоким напряжениям  поведение продукта будет все больше напоминать поведение жидкообразных продуктов. Величина предела текучести зависит от концентрации дисперсной фазы в структуре продукта, а вязкость при переходе через предел текучести определяется вязкостью дисперсной среды.
поведение продукта будет все больше напоминать поведение жидкообразных продуктов. Величина предела текучести зависит от концентрации дисперсной фазы в структуре продукта, а вязкость при переходе через предел текучести определяется вязкостью дисперсной среды.
Пластичные вещества, такие как жиры, масла, пасты и др. обладают сопротивлением текучести, и для них существует предел текучести. Для таких веществ применим закон Бингхэма  , где
, где  - напряжение сдвига при пределе текучести.
- напряжение сдвига при пределе текучести.
На рис. 3.4. приведены зависимости неньютоновых пищевых продуктов, у которых свойства не зависят от продолжительности сдвига. К таким продуктам относятся:
- вязкие пищевые продукты (кривая течения 4). У этих продуктов зависимость напряжения сдвига от скорости деформации линейный характер и отсекает на оси ординат отрезок равный  , называемый пределом текучести
, называемый пределом текучести 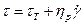 , где
, где  - пластическая вязкость. Продукты, с таким поведением относят к идеально-пластичным материалам или телам Шведова - Бингама. Если напряжение сдвига будет меньше предела текучести, то такие тела остаются неподвижными или могут перемещаться как твердое тело.
- пластическая вязкость. Продукты, с таким поведением относят к идеально-пластичным материалам или телам Шведова - Бингама. Если напряжение сдвига будет меньше предела текучести, то такие тела остаются неподвижными или могут перемещаться как твердое тело.

Рис. 3.4. Зависимости напряжения сдвига от скорости сдвига
1 – упрочняющиеся псевдопластичные продукты, 2 – ньютонова жидкость, 3 – псевдопластичные пищевые продукты, 4 – вязкие пищевые продукты, 5 – смешанный тип продуктов
- кривая течения 5 соответствует нелинейным вязкопластичным телам. Зависимость напряжения сдвига  от скорости деформации
от скорости деформации  у таких тел выражается как
у таких тел выражается как  (уравнение Шульмана) или
(уравнение Шульмана) или  , где
, где  - коэффициент и показатель степени определяются экспериментально (уравнение Хершеля-Балкли);
- коэффициент и показатель степени определяются экспериментально (уравнение Хершеля-Балкли);
- псевдопластичные пищевые продукты (кривая 3). Поведение таких продуктов при напряжениях выше предела текучести называется пластичностью смешанного типа. Примерами псевдопластичных неньютоновских жидкостей является сгущенное молоко, различного вида пюре, кетчуп и пр.
|
|
|
- реологическое поведение упрочняющихся пищевых продуктов (кривая 1) обратно псевдопластичным продуктам.
Ниже (табл. 3.1) в качестве примера приведены числовые значения вязкости  , показателя
, показателя  и предела текучести
и предела текучести  для некоторых пищевых продуктов, описываемых неньютоновой моделью реологического поведения.
для некоторых пищевых продуктов, описываемых неньютоновой моделью реологического поведения.
Таблица 3.1.
Реологические параметры некоторых неньютоновых жидкостей
| Наименование продукта | Эффективная вязкость  , мПа·с , мПа·с
| Показатель степени для течения жидкости, 
| Коэффициент консистенции, 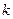
| Предел текучести,  , Па , Па
|
| Яблочное пюре Сок томатный Томатная паста Молоко сгущенное Йогурт Сливочное масло Мясо (30% жира) | 0,15…0,24 0,40 0,28 0,834 0,46 0,042 0,341 | 40,6…76,9 139…252 1,31 417,0 160,2 | 18,4…50,7 78…212 3,97 1,16 27,8 |
Таким образом, к жидкостям относятся сложные реологические среды, при деформировании которых могут возникать следующие эффекты:
- неньютоновская вязкость при установившемся течении,
- упругость,
- структурные преобразования,
- существование пределов течения.
Материал относится к жидкости:
- если он обладает вязким течением и необратимые деформации в нем возникают при любых напряжениях по величине, т.е. жидкость не запасает работу внешних сил и вязкое сопротивление означает диссипацию этой работы. К вязким жидкостям относятся среды, в которых затраченная на их деформирование энергия полностью диссипирует, переходя в тепло;
- если часть затраченной на деформирование материала работы сохраняется в виде упругих деформаций, то такой материал может быть отнесен в общем случае к вязкоупругим телам в т.ч. и к вязкоупругим жидкостям;
- пластичные материалы могут рассматриваться как жидкости в том случае, если в них необратимые деформации будут наблюдаться после перехода напряжений за предел текучести.
|
|
|


