 |
Передача теплоты теплопроводностью
|
|
|
|
В общем случае процесс передачи теплоты теплопроводностью в твердом теле сопровождается изменением температуры тела 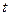 в пространстве и во времени, т.е.
в пространстве и во времени, т.е. 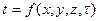 . Данная функция определяет температурное поле.
. Данная функция определяет температурное поле.
Если температура будет являться функцией координат и времени, то температурное поле является нестационарным, т.е. зависящим от времени 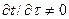 , если температура не изменяется с течением времени, то поле стационарно
, если температура не изменяется с течением времени, то поле стационарно 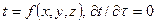 .
.
Если температура тела является функцией двух координат, то температурное поле для стационарного режима 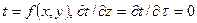 ; а для нестационарного
; а для нестационарного 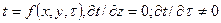 .
.
Для одномерного случая, например, при переносе теплоты через стенку аппарата, у которой длина и ширина являются бесконечно большими величинами по сравнению с толщиной, уравнение температурного поля для стационарного режима запишется как 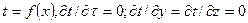 , а для нестационарного
, а для нестационарного 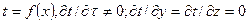 .
.
Если в теле соединить точки с одинаковой температурой линиями (изотермами), то поверхность равных температур называется изотермной поверхностью. Изотермные поверхности не пересекаются друг с другом. При рассмотрении двух изотермных поверхностей можно заметить, что интенсивность изменения температуры по разным направлениям неодинакова. Наибольшее изменение (наибольшая разность на единицу длины) наблюдается в направлении нормали к изотермной поверхности.
Предел отношения изменения температуры 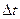 к расстоянию между изотермами по нормали
к расстоянию между изотермами по нормали 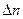 при
при 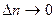 , называется градиентом температуры
, называется градиентом температуры 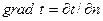 , (град/м).
, (град/м).
Градиент - это вектор, направленный по нормали к изотермной поверхности в сторону увеличения температуры, численно равный производной от температуры по этому направлению.
При передаче теплоты теплопроводностью градиент температуры в разных точках тела не должен быть равен нулю. Связь между количеством теплоты  , проходящей через элементарную площадку
, проходящей через элементарную площадку 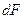 на изотермной поверхности за промежуток времени
на изотермной поверхности за промежуток времени  , и градиентом температуры устанавливается зависимостью Фурье (основной закон теплопроводности)
, и градиентом температуры устанавливается зависимостью Фурье (основной закон теплопроводности) 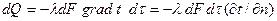 . Здесь минус показывает, что в направлении теплового потока температура убывает и градиент отрицателен.
. Здесь минус показывает, что в направлении теплового потока температура убывает и градиент отрицателен.
|
|
|
Величина 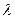 является коэффициентом пропорциональности, называемым коэффициентом теплопроводности, Вт/(м∙град). Числовое значение коэффициента определяет количество теплоты, проходящей через единицу изотермной поверхности в единицу времени, при условии, что градиент температуры равен единице. Коэффициент теплопроводности зависит от давления и температуры и определяется опытным путем, его значения приводятся в справочных таблицах.
является коэффициентом пропорциональности, называемым коэффициентом теплопроводности, Вт/(м∙град). Числовое значение коэффициента определяет количество теплоты, проходящей через единицу изотермной поверхности в единицу времени, при условии, что градиент температуры равен единице. Коэффициент теплопроводности зависит от давления и температуры и определяется опытным путем, его значения приводятся в справочных таблицах.
Количество теплоты, проходящее через единицу изотермной поверхности в единицу времени, называется плотностью теплового потока или вектором плотности теплового потока, его размерность Вт/м2:  . Этот вектор направлен по нормали к изотермной поверхности в сторону убывания температуры.
. Этот вектор направлен по нормали к изотермной поверхности в сторону убывания температуры.
Выше было дано определение теплового потока как потока внутренней энергии, передаваемой теплоносителем нагреваемому продукту в результате их контакта или облучения. Более строгое определение теплового потока - это количество теплоты, прошедшее в единицу времени через произвольную поверхность 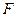 , (Вт):
, (Вт): 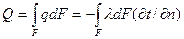 .
.
Для определения количества теплоты, проходящей через какую-то произвольную поверхность тела, необходимо знать температурное поле внутри этого тела, что и составляет основную аналитическую задачу теории теплопроводности.
В нестационарном температурном поле без тепловых источников связь между величинами, участвующими в передаче теплоты теплопроводностью для точки 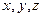 , устанавливается дифференциальным уравнением теплопроводности
, устанавливается дифференциальным уравнением теплопроводности  или
или 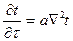 , где
, где 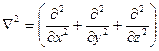 - «набла» - оператор Лапласа;
- «набла» - оператор Лапласа; 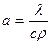 , (м2/сек) - коэффициент температуропроводности.
, (м2/сек) - коэффициент температуропроводности.
|
|
|
Уравнение 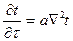 для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты является основным уравнением при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты теплопроводностью, устанавливающим связь между временным и пространственным изменением температуры в любой точке поля.
для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты является основным уравнением при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты теплопроводностью, устанавливающим связь между временным и пространственным изменением температуры в любой точке поля.
Дифференциальное уравнение теплопроводности с источниками теплоты внутри тела имеет вид  , где
, где 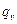 - количество выделяемой теплоты в единице объема вещества в единицу времени, Вт/м3, с – массовая теплоемкость тела, Дж/(кг∙град);
- количество выделяемой теплоты в единице объема вещества в единицу времени, Вт/м3, с – массовая теплоемкость тела, Дж/(кг∙град);  - плотность вещества, кг/м3.
- плотность вещества, кг/м3.
Для применения уравнения в конкретном случае нужно знать форму и размеры тела, физические параметры среды и тела, начальные условия, т.е. распределение температур в теле в начальный момент времени, и граничные условия, которые характеризуют распределение температур на поверхности тела или его взаимодействие со средой. В совокупности эти условия называются условиями однозначности или краевыми условиями. Обычно принимают в начальный момент времени 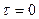 .
.
Граничные условия могут быть заданы тремя способами:
- граничное условие первого рода задается распределением температуры на поверхности тела для любого момента времени;
- граничное условие второго рода задается плотностью теплового потока в каждой точке поверхности тела для любого момента времени;
- граничное условие третьего рода задается температурой среды, окружающей тело, и законом теплоотдачи между поверхностью и средой. В соответствии с законом сохранения энергии количество теплоты, отданное единицей поверхности окружающей среде в единицу времени должно быть равно теплоте, подводимой путем теплопроводности к этой единице поверхности со стороны внутренних частей тела в единицу времени 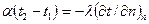 , где
, где 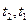 - температура поверхности тела и среды соответственно,
- температура поверхности тела и среды соответственно,  - проекция градиента температуры к площадке.
- проекция градиента температуры к площадке.
Рассмотрим некоторые типовые случаи теплопередачи:
Случай 1 - Плоская стенка (рис.4.2). Пусть рассматриваемая стенка имеет одинаковую толщину 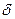 с одинаковыми температурами поверхностей
с одинаковыми температурами поверхностей 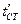 ,
, 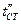 и постоянным коэффициентом теплопроводности
и постоянным коэффициентом теплопроводности 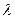 . Температура изменяется в направлении перпендикулярном плоскости стенки и в любой точке тела является неизменной и не зависящей от времени
. Температура изменяется в направлении перпендикулярном плоскости стенки и в любой точке тела является неизменной и не зависящей от времени  .
.
|
|
|
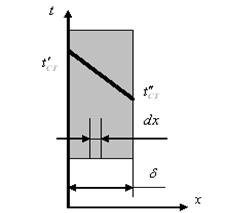
Рис.4.2. Схема теплопередачи через плоскую тонкую стенку
Учитывая, что 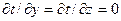 и
и  , уравнение теплопроводности имеет вид
, уравнение теплопроводности имеет вид 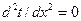 . Его решение дает
. Его решение дает 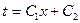 , т.е. при постоянном коэффициенте теплопроводности закон изменения температуры при передаче теплоты через плоскую стенку является линейным.
, т.е. при постоянном коэффициенте теплопроводности закон изменения температуры при передаче теплоты через плоскую стенку является линейным.
Постоянные интегрирования 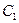 и
и 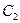 : при
: при  температура стенки равна
температура стенки равна 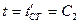 , а при
, а при 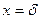 температура будет
температура будет 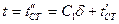 . Откуда
. Откуда 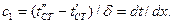
Плотность теплового потока 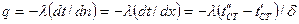 или
или 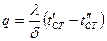 .
.
Общее количество теплоты, передаваемое теплопроводностью через плоскую стенку с поверхностью 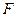 за время
за время  равно
равно
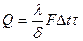 , где
, где 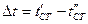 - температурный напор.
- температурный напор.
В реальных условиях коэффициент теплопроводности зависит от температуры и закон ее изменения в стенке выражается кривой линией. При переменном коэффициенте теплопроводности (считая зависимость линейной 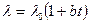 ) плотность теплового потока выражается формулой
) плотность теплового потока выражается формулой 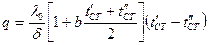 . Здесь множитель
. Здесь множитель  - среднеинтегральная величина коэффициента теплопроводности.
- среднеинтегральная величина коэффициента теплопроводности.
Уравнение температурной кривой в стенке 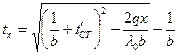 . При отрицательном коэффициенте
. При отрицательном коэффициенте 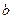 кривая направлена выпуклостью вниз.
кривая направлена выпуклостью вниз.
Случай 2 - Многослойная плоская стенка (рис.4.3). Формула теплопроводности многослойной стенки выводится из уравнения теплопроводности для отдельных слоев при допущении, что тепловой поток, проходящий через любую изотермную поверхность неоднородной стенки, одинаков.

Рис.4.4.Схема теплопередачи через многослойную плоскую стенку
Тепловой поток для каждого слоя

Выразив эти уравнения относительно разности температур, и сложив, найдем 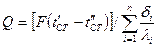 , где
, где 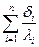 - полное термическое сопротивление многослойной стенки.
- полное термическое сопротивление многослойной стенки.
Температуры между отдельными слоями стенки равны 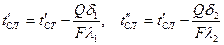 и т.д.
и т.д.
Случай 3 - Однослойная цилиндрическая стенка (рис. 4.4). Пусть труба имеет бесконечную длину. В этом случае температурное поле можно принять одномерным 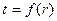 , где
, где 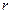 текущая цилиндрическая координата. Температуры на внешней
текущая цилиндрическая координата. Температуры на внешней 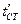 и внутренней
и внутренней 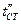 поверхностях трубы постоянны. Изотермные поверхности представляют собой концентрические поверхности с общей осью трубы. Температура меняется в направлении радиуса, и тепловой поток радиален.
поверхностях трубы постоянны. Изотермные поверхности представляют собой концентрические поверхности с общей осью трубы. Температура меняется в направлении радиуса, и тепловой поток радиален.
|
|
|
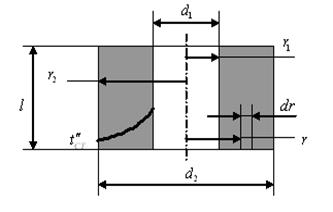
Рис. 4.4 Схема теплопередачи через цилиндрическую стенку трубы
Выделим внутри трубы элементарный кольцевой слой радиусом 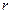 и толщиной
и толщиной 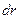 , тогда можно рассматривать этот слой как плоскую стенку, разность температур между поверхностями которого будет также бесконечно малой и равной
, тогда можно рассматривать этот слой как плоскую стенку, разность температур между поверхностями которого будет также бесконечно малой и равной 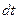 .
.
Отсюда  или для кольцевого слоя
или для кольцевого слоя 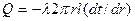 . Разделив переменные, получим уравнение
. Разделив переменные, получим уравнение  , интегрируя которое в пределах
, интегрируя которое в пределах  и
и  , найдем решение
, найдем решение 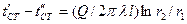 , откуда
, откуда 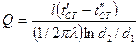 .
.
Тепловой поток относительно единицы длины трубы 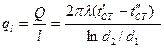 , относительно внутренней
, относительно внутренней 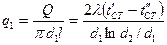 или внешней
или внешней  поверхности.
поверхности.
Случай 4 - Многослойная цилиндрическая стенка. Пусть имеется трехслойная труба, у которой внутренний диаметр равен 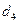 , диаметры слоев
, диаметры слоев 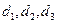 , температура внутренней поверхности стенки равна
, температура внутренней поверхности стенки равна 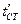 , наружной
, наружной 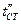 , коэффициенты теплопроводности слоев соответственно
, коэффициенты теплопроводности слоев соответственно  . Температура каждого слоя изменяется по логарифмической кривой и через них проходит один и тот же тепловой поток.
. Температура каждого слоя изменяется по логарифмической кривой и через них проходит один и тот же тепловой поток.
Из уравнений теплового потока для каждого слоя, разрешив их относительно разностей температур и почленно сложив, получим 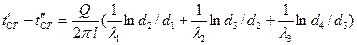 , откуда находится величина
, откуда находится величина 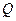 . Для многослойной цилиндрической стенки с n слоями
. Для многослойной цилиндрической стенки с n слоями 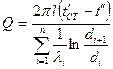 .
.
Температуры между слоями находятся по формулам 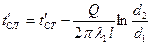 и т. д.
и т. д.
Пример: Стальная труба (коэффициент теплопроводности 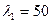 Вт/(м∙град)
Вт/(м∙град)  мм) покрыта двумя слоями изоляции. Толщина первого слоя составляет
мм) покрыта двумя слоями изоляции. Толщина первого слоя составляет 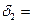 5 мм с
5 мм с 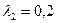 Вт/(м∙град), второго 10 мм с
Вт/(м∙град), второго 10 мм с  Вт/(м∙град). Температура внутренней поверхности трубы
Вт/(м∙град). Температура внутренней поверхности трубы  , наружной поверхности изоляции
, наружной поверхности изоляции 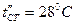 .
.
Требуется найти потери теплоты через изоляцию с одного метра трубы и температуры на границе слоев.
Имеем 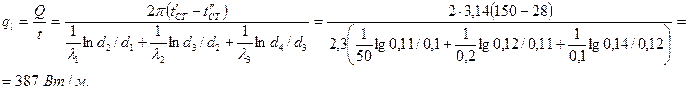 Температура между слоями изоляции
Температура между слоями изоляции
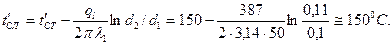
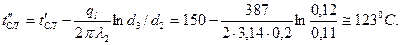
Рассмотрим процесс теплопередачи через плоскую однослойную стенку при граничных условиях третьего рода (рис. 4.5).
При теплопередаче теплота передается всеми тремя способами: теплопроводностью, конвекцией и излучением. Первый этап теплопередачи при наличии стенки – перенос теплоты конвекцией от горячего теплоносителя к стенке. Конвекция сопровождается теплопроводностью и излучением. На втором этапе осуществляется перенос теплоты теплопроводностью через стенку (если материал стенки пористый, то теплопроводность связана с конвекцией и излучением в порах). Третий этап связан переносом теплоты конвекцией от второй поверхности стенки к холодному теплоносителю, что также сопровождается теплопроводностью и излучением.
Количество теплоты, передаваемое конвекцией, определяется уравнением Ньютона-Рихмана  , где
, где 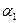 - коэффициент теплоотдачи от горячего теплоносителя с температурой
- коэффициент теплоотдачи от горячего теплоносителя с температурой  к поверхности стенки,
к поверхности стенки, 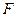 - расчетная поверхность плоской стенки, м2.
- расчетная поверхность плоской стенки, м2.
|
|
|
Тепловой поток, переданный теплопроводностью, через стенку равен 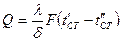 .
.
Тепловой поток от второй поверхности стенки к холодному теплоносителю  , где
, где  - коэффициент теплоотдачи от второй поверхности стенке к среде с температурой
- коэффициент теплоотдачи от второй поверхности стенке к среде с температурой 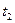 .
.
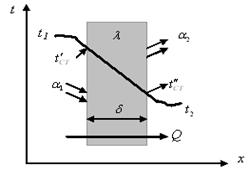
Рис.4.5 Схема теплопередачи через плоскую однослойную стенку
Все три величины 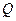 одинаковы – сколько теплоты воспринимает стенка, столько она и отдает в стационарном режиме, поэтому, решая все три уравнения относительно разностей температур и складывая их почленно, получим
одинаковы – сколько теплоты воспринимает стенка, столько она и отдает в стационарном режиме, поэтому, решая все три уравнения относительно разностей температур и складывая их почленно, получим 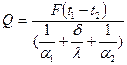 или
или  , где
, где 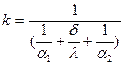 - коэффициент теплопередачи, Вт/(м2∙град).
- коэффициент теплопередачи, Вт/(м2∙град).
Плотность теплового потока  .
.
Коэффициент теплопередачи 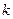 выражает количество теплоты, проходящее через единицу поверхности стенки в единицу времени от горячего к холодному теплоносителю при разности температур между ними в 1оС.
выражает количество теплоты, проходящее через единицу поверхности стенки в единицу времени от горячего к холодному теплоносителю при разности температур между ними в 1оС.
Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением 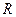 .
.
Известно, что тепловые потери снижаются пропорционально увеличению толщины изоляционного слоя, поэтому для тепловой изоляции должны использоваться материалы с низким коэффициентом теплопроводности. Критический диаметр слоя изоляции не зависит от диаметра трубопровода, он будет тем меньше, чем меньше коэффициент теплопроводности изоляции и чем больше коэффициент теплоотдачи  ;
; 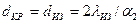 . Для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше внешнего диаметра оголенного трубопровода.
. Для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше внешнего диаметра оголенного трубопровода.
Пример: Для изоляции патрубка продуктопровода диаметром 30 мм имеется изоляционный материал с коэффициентом теплопроводности  = 0,1 Вт/(м∙град). Коэффициент теплоотдачи составляет
= 0,1 Вт/(м∙град). Коэффициент теплоотдачи составляет 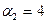 Вт/(м2∙град).
Вт/(м2∙град).
Определить целесообразность применения данного изоляционного материала. Критический диаметр изоляции 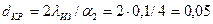 м.
м.
Поскольку  данный материал применять нецелесообразно.
данный материал применять нецелесообразно.
Ребристые поверхности в машинах и аппаратах пищевых производств применяют для выравнивания термических сопротивлений теплоотдачи с обеих сторон стенки, например, когда с одной стороны стенки находится жидкость с большим коэффициентом теплоотдачи, а с другой газ с малым коэффициентом, создающим значительное термическое сопротивление. Поэтому оребрение стенки со стороны большего термического сопротивления позволяет увеличить поверхность соприкосновения с теплоносителем и увеличить тем самым тепловой поток.
Коэффициент эффективности ребер равен отношению количества теплоты, передаваемой поверхностью ребер в окружающую среду, к теплоте, которую эта поверхность могла бы передать при постоянной температуре, равной температуре у основания ребер  . Отношение оребренной поверхности
. Отношение оребренной поверхности 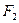 к гладкой
к гладкой 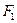 называется коэффициентом оребрения.
называется коэффициентом оребрения.
Пример: Пусть имеется стенка толщиной 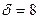 мм, коэффициент оребрения которой равен
мм, коэффициент оребрения которой равен 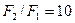 . Материал стенки серый чугун, коэффициент теплопроводности которого равен
. Материал стенки серый чугун, коэффициент теплопроводности которого равен 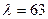 Вт/(м∙град). Коэффициент теплоотдачи от рабочего тела к стенке
Вт/(м∙град). Коэффициент теплоотдачи от рабочего тела к стенке  Вт/(м2∙град) и
Вт/(м2∙град) и  10 Вт/(м2∙град). Температура рабочего тела
10 Вт/(м2∙град). Температура рабочего тела  =100оС, температура окружающей среды
=100оС, температура окружающей среды  С.
С.
Коэффициент теплопередачи при отнесении теплового потока к гладкой поверхности  Вт/(м2∙град).
Вт/(м2∙град).
Плотность теплового потока  Вт/м2.
Вт/м2.
Коэффициент теплопередачи при условии плоской стенки 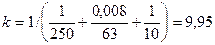 Вт/(м2∙град).
Вт/(м2∙град).
Плотность теплового потока для плоской стенки 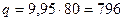 Вт/м2.
Вт/м2.
Можно видеть, что оребрение увеличивает теплопередачу примерно в 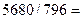 7 раз.
7 раз.
|
|
|


