 |
Признак существования конечного предела последовательности
|
|
|
|
Для того, чтобы последовательность  имела конечный предел a, необходимо и достаточно, чтобы эта последовательность представлялась как сумма числа a и бесконечно малой последовательности:
имела конечный предел a, необходимо и достаточно, чтобы эта последовательность представлялась как сумма числа a и бесконечно малой последовательности:

Теорема Вейерштрасса о пределе монотонной последовательности

Аудиторные задания
Задача 1
Среди данных последовательностей  укажите номера последовательностей:
укажите номера последовательностей:
а) сходящихся, б) расходящихся, в) бесконечно малых, г) бесконечно больших,
д) ограниченных, е) монотонных:
1)  2)
2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 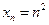 ; 6)
; 6)  ; 7)
; 7)  ;
;
8)  9)
9)  10)
10) 
Ответ: а) сходящиеся последовательности: 1), 2), 8), 9), 10);
б) расходящиеся последовательности: 3), 4), 5), 6), 7);
в) бесконечно малые последовательности: 1), 2), 8), 9);
г) бесконечно большие последовательности: 3), 5), 7);
д) ограниченные последовательности: 1), 2), 6), 8), 9), 10);
е) монотонные последовательности: 1), 5), 7), 8), 10).
Задача 2
Используя определение предела последовательности докажите, что
1) 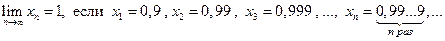
2) 
3)  является бесконечно малой, если
является бесконечно малой, если 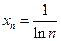 ;
;
4)  является бесконечно большой, если
является бесконечно большой, если  .
.
Задача 3
Используя признак существования конечного предела последовательности, докажите, что
1)  2)
2)  3)
3)  4)
4) 
Задача 4
Используя теорему Вейерштрасса, докажите, что следующие последовательности являются сходящимися:
1)  ;
;
2)  .
.
Задания для домашнего выполнения
Задача 1
Среди данных последовательностей  укажите номера последовательностей:
укажите номера последовательностей:
а) сходящихся, б) расходящихся, в) бесконечно малых, г) бесконечно больших,
д) ограниченных, е) монотонных:
1)  2)
2) 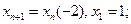 3)
3)  ; 4)
; 4) 
5)  6)
6)  ; 7)
; 7) 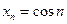 ; 8)
; 8)  ;
;
9)  ; 10)
; 10) 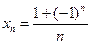 .
.
Задача 2
Используя определение предела последовательности докажите, что
1)  является бесконечно большой, если
является бесконечно большой, если  ;
;
2)  является бесконечно малой, если
является бесконечно малой, если  ;
;
3)  , если
, если 
4)  , если
, если  ;
;
5)  если
если  ;
;
6)  если
если  .
.
Задача 3
|
|
|
Используя признак существования конечного предела последовательности, докажите, что:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Задача 4
Используя теорему Вейерштрасса, докажите, что следующие последовательности являются сходящимися:
1) 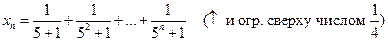
2) 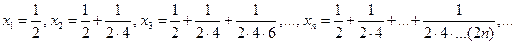 ;
;
Ответы к задачам для домашнего выполнения
Задача 1
а) сходящиеся последовательности: 1), 3), 5), 6), 8), 10);
б) расходящиеся последовательности: 2), 4), 7), 9);
в) бесконечно малые последовательности: 1), 6), 8), 10);
г) бесконечно большие последовательности: 2);
д) ограниченные последовательности: 1), 3), 4), 5), 6), 7), 8), 10);
е) монотонные последовательности: 3), 6), 8).
Задача 4
1) 

 конечный
конечный  - сходящаяся последовательность;
- сходящаяся последовательность;
2) 



 конечный
конечный  сходится.
сходится.
Занятие 2. Вычисление пределов последовательностей с помощью свойств сходящихся, бесконечно малых, бесконечно больших и ограниченных последовательностей
Цель занятия:
1) использовать основные свойства сходящихся, бесконечно малых, бесконечно больших и ограниченных последовательностей для вычисления предела заданной последовательности;
2) рассмотреть примеры раскрытия неопределенностей 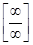 и
и  для последовательностей.
для последовательностей.
Краткие теоретические сведения
- Основные теоремы о сходящихся последовательностях:
1) 


2) 


 .
.
- Основные теоремы о бесконечно малых последовательностях:
1) если последовательности  и
и  являются бесконечно малыми, то их сумма
являются бесконечно малыми, то их сумма  и их произведение
и их произведение 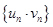 также являются бесконечно малыми последовательностями, т.е.
также являются бесконечно малыми последовательностями, т.е.

2) если последовательность  является бесконечно малой, а последовательность
является бесконечно малой, а последовательность  – ограниченной, то их произведение
– ограниченной, то их произведение 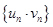 является бесконечно малой последовательностью, т.е.
является бесконечно малой последовательностью, т.е.
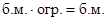
3) если последовательность  является бесконечно малой и
является бесконечно малой и 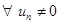 , то последовательность
, то последовательность 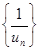 является бесконечно большой, т.е.
является бесконечно большой, т.е.

- Основные теоремы о бесконечно больших последовательностях:
1) если последовательности  и
и  являются бесконечно большими, причем
являются бесконечно большими, причем  (т.е. числа un и vn всегда одного знака), то их сумма
(т.е. числа un и vn всегда одного знака), то их сумма  также является бесконечно большой последовательностью, т.е.
также является бесконечно большой последовательностью, т.е.
|
|
|

 | |||
 |
одного знака
2) если  и
и  – две бесконечно большие последовательности, то их произведение
– две бесконечно большие последовательности, то их произведение  также является бесконечно большой последовательностью, т.е.
также является бесконечно большой последовательностью, т.е.

3) если  – бесконечно большая последовательность,
– бесконечно большая последовательность,  – ограниченная последовательность, то их сумма
– ограниченная последовательность, то их сумма  есть бесконечно большая последовательность и их произведение
есть бесконечно большая последовательность и их произведение  тоже бесконечно большая последовательность, но при дополнительном условии, что ограниченная
тоже бесконечно большая последовательность, но при дополнительном условии, что ограниченная  не является бесконечно малой последовательностью, т.е.
не является бесконечно малой последовательностью, т.е.

4) если  – бесконечно большая последовательность, причем
– бесконечно большая последовательность, причем 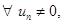 то последовательность
то последовательность 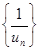 является бесконечно малой, т.е.
является бесконечно малой, т.е.

Аудиторные задания
Задача 1
Вычислите следующие пределы последовательностей, используя основные теоремы о свойствах сходящихся последовательностей, бесконечно малых, бесконечно больших и ограниченных последовательностей (в процессе решения указывайте используемые свойства в каждом пределе):
1)  ; 2)
; 2) 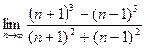 ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ; 9)
; 9)  ;
;
10)  ; 11)
; 11) 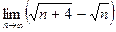 ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ; 15)
; 15)  .
.
Ответы: 1) 0,5; 2) 3; 3)  ; 4) 0; 5) 1; 6) 0; 7) 4/3;
; 4) 0; 5) 1; 6) 0; 7) 4/3;
8) -1/2; 9) 1; 10) 0; 11) 0; 12) 0,5; 13) 0; 14) 0; 15) 2.
|
|
|


