 |
Задания для домашнего выполнения
|
|
|
|
Задача 1
Постройте график кусочно-заданной функции и по графику опишите свойство непрерывности этой функции; сформулируйте при этом рабочие определения:
1) 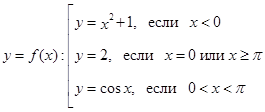 2)
2) 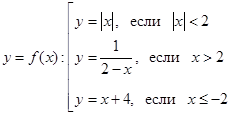
Задача 2
Исследуйте непрерывность элементарной функции, используя основные свойства непрерывных функций; построите часть графика функции в окрестности каждой точки разрыва:
1) 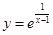 ; 2)
; 2) 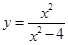 ;
;
Задание 3
Решите следующие задачи (Берман №222, №223, №227, №228, №229):
1. Три цилиндра, радиусы оснований которых соответственно равны 3, 2 и 1 м, а высоты одинаковы и равны 5 м, поставлены друг на друга. Выразить площадь поперечного сечения  получившегося тела как функцию расстояния
получившегося тела как функцию расстояния  этого сечения от нижнего основания нижнего цилиндра. Будет ли эта функция непрерывной?
этого сечения от нижнего основания нижнего цилиндра. Будет ли эта функция непрерывной?
2. Функция 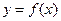 содержит параметр a:
содержит параметр a:
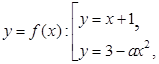
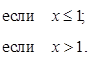
При каком выборе числа 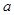 функция
функция  будет непрерывной?
будет непрерывной?
3.Какого рода разрывы имеют функции  и
и 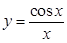 при
при  ? Укажите характер графиков этих функций в окрестности точки
? Укажите характер графиков этих функций в окрестности точки  .
.
4. Исследуйте непрерывность функции, заданной так:  при
при 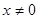 ,
, 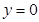 при
при  . Постройте график этой функции.
. Постройте график этой функции.
5.Сколько точек разрыва (и какого рода) имеет функция  ? Постройте её график.
? Постройте её график.
Ответы к заданиям для домашнего выполнения
Задача 1
1) Функция 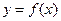 является непрерывной на промежутках
является непрерывной на промежутках 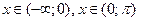 и
и
 ; в точке
; в точке 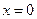 имеет разрыв типа выколотой точки, т.к.
имеет разрыв типа выколотой точки, т.к. 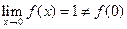 ; в точке
; в точке 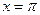 имеет разрыв типа скачка, т.к.
имеет разрыв типа скачка, т.к.  .
.
2) Функция 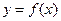 является непрерывной при
является непрерывной при  и при
и при 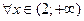 , в точке
, в точке 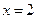 имеет бесконечный разрыв, т.к.
имеет бесконечный разрыв, т.к.  .
.
Задача 2
1)

| Функция 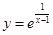 является непрерывной при является непрерывной при 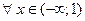 и при и при 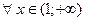 , в точке x = 1 – имеет бесконечный разрыв; , в точке x = 1 – имеет бесконечный разрыв;
 , ,  . .
|
2)
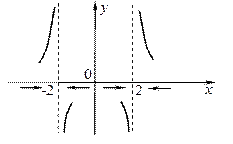
| Функция 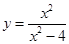 непрерывна на каждом из промежутков непрерывна на каждом из промежутков  и имеет бесконечные разрывы в точках и имеет бесконечные разрывы в точках  и и 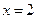 . .
|
Задача 3
1. 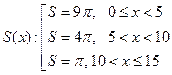 , функция
, функция  имеет разрывы типа скачка при x = 5 и x = 10.
имеет разрывы типа скачка при x = 5 и x = 10.
|
|
|
2. При a = 1.
3.Функция 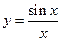 имеет в точке
имеет в точке 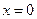 разрыв первого рода (типа выколотой точки);
разрыв первого рода (типа выколотой точки);
функция  имеет в точке
имеет в точке 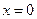 разрыв второго рода (бесконечный).
разрыв второго рода (бесконечный).
4. Функция является непрерывной при всех  и имеет разрыв типа скачка при x = 0.
и имеет разрыв типа скачка при x = 0.
5. Функция имеет три точки разрыва: 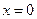 - точка разрыва первого рода (устранимый разрыв),
- точка разрыва первого рода (устранимый разрыв), 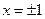 - точки разрыва второго рода (бесконечные разрывы).
- точки разрыва второго рода (бесконечные разрывы).
Занятие 10. Контрольная работа
Цель занятия:
провести контрольную работу по теме: «Предел и непрерывность функций одной переменной»
Контрольная работа «Предел и непрерывность функций одной переменной»,
вариант 0
Задача 1
Вычислите 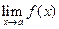 , ответы проиллюстрируйте возможным локальным поведением графика функции
, ответы проиллюстрируйте возможным локальным поведением графика функции 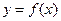 в окрестности точки
в окрестности точки  :
:
1)  ; 2)
; 2)  ;
;
3*)  ; 4)
; 4) 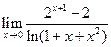 .
.
Задача 2
Сравните бесконечно малые функции при  :
:
1)  ,
, 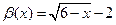 ,
,  ;
;
2*)  ,
, 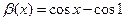 ,
,  .
.
Задача 3
1) По графику функции 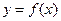 опишите ее непрерывность:
опишите ее непрерывность:
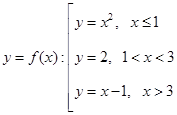 .
.
2) Проведите исследование функции на непрерывность, постройте часть ее графика в окрестности точки разрыва: 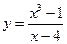 .
.
Задача 4
Используя строгое определение предела функции по Коши (на языке  ), докажите, что
), докажите, что  .
.
Ответы к задачам 0 варианта контрольной работы
«Предел и непрерывность функций одной переменной»
Задача 1
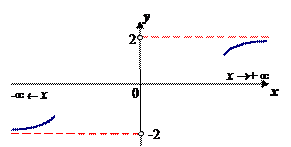 1)
1) 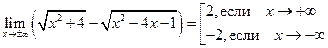
значения функции 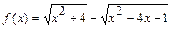
сколь угодно близки к числу 2 при достаточно больших положительных значениях x и сколь угодно близки к числу -2 при достаточно больших по модулю отрицательных значениях x.
2) 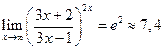
 значения функции
значения функции 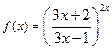 становятся сколь угодно близкими к числу e2, если значения аргумента x будутдостаточно большими по модулю.
становятся сколь угодно близкими к числу e2, если значения аргумента x будутдостаточно большими по модулю.
3*) 
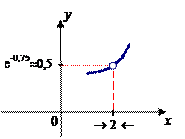 значения функции
значения функции 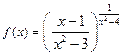 сколь угодно мало отличаются от числа
сколь угодно мало отличаются от числа 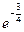 для значений аргумента x, достаточно близких к числу 2 (но
для значений аргумента x, достаточно близких к числу 2 (но 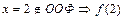 не существует).
не существует).
4) 
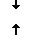
 значения функции
значения функции  сколь угодно мало отличаются от числа
сколь угодно мало отличаются от числа 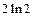 , если значения аргумента x будут достаточно близкими к числу 0
, если значения аргумента x будут достаточно близкими к числу 0
(но  не существует).
не существует).
Задача 2
1) 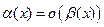 при
при  , то есть б.м. функция
, то есть б.м. функция 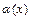 имеет более высокий порядок малости по сравнению с б.м. функцией
имеет более высокий порядок малости по сравнению с б.м. функцией  , при
, при  ;
;
|
|
|
2*)  при
при  , то есть б.м. функции
, то есть б.м. функции 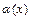 и
и  при
при  имеют одинаковый порядок малости.
имеют одинаковый порядок малости.
Задача 3
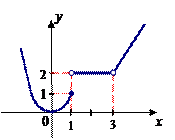
1)
Функция 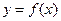 является непрерывной при
является непрерывной при 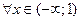 ,
, 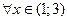 и
и 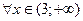 ; при
; при  функция имеет разрыв типа скачка, при
функция имеет разрыв типа скачка, при 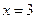 – разрыв типа выколотой точки.
– разрыв типа выколотой точки.
2)

| Функция 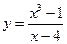 является непрерывной при является непрерывной при 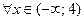 и при и при 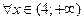 , имеет бесконечный разрыв в точке , имеет бесконечный разрыв в точке 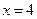 . .
|
Задача 4
 , так как
, так как 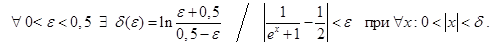
|
|
|


