 |
Задания для домашнего выполнения
|
|
|
|
Задача 1
Вычислите пределы функций f (x), используя теоремы о функциях, имеющих конечные пределы, о бесконечно малых, бесконечно больших и локально ограниченных функциях; результат вычисления проиллюстрируйте возможным локальным поведением графика функции f (x) в окрестности той точки, в которой вычисляется предел; опишите словами смысл иллюстрации:
1)  ; 2)
; 2) 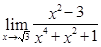 ; 3)
; 3) 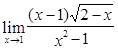 ;
;
4) 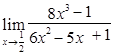 ; 5)
; 5)  ; 6)
; 6) 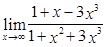 ;
;
7) 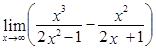 ; 8)
; 8) 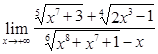 ; 9)
; 9) 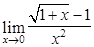
10)  ; 11)
; 11)  ; 12)
; 12)  ;
;
13) 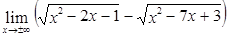 .
.
Ответы к заданиям для домашнего выполнения
Задача 1
1) 3/4; 2) 0; 3) 0,5; 4) 6; 5) ∞; 6) -1; 7) 0,25; 8) ∞; 9) ∞;
10) 0,25; 11) 1/3; 12) 1/2, если x→+∞; -∞, если x→-∞;
13) 5/2, если x→+∞; - 5/2, если x→-∞.
Занятие 6. Основные правила раскрытия неопределенностей. Замечательные пределы. Раскрытие неопределенностей с помощью замены эквивалентных бесконечно малых
Цель занятия:
1) сформулировать основные правила раскрытия неопределенностей;
2) рассмотреть раскрытие неопределенности  с помощью 2-го замечательного предела;
с помощью 2-го замечательного предела;
3) отработать раскрытие неопределенности 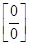 с помощью замены эквивалентных бесконечно малых.
с помощью замены эквивалентных бесконечно малых.
Краткие теоретические сведения
1. Правила раскрытия основных неопределенностей:
Правило 1. Чтобы раскрыть неопределенность 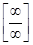 , образованную при
, образованную при  делением целых многочленов или иррациональных функций, нужно в числителе и в знаменателе вынести за скобки переменную в старших степенях и провести сокращение этих степеней.
делением целых многочленов или иррациональных функций, нужно в числителе и в знаменателе вынести за скобки переменную в старших степенях и провести сокращение этих степеней.
Правило 2. Чтобы раскрыть неопределенность 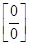 , образованную при
, образованную при 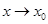 делением целых многочленов или иррациональных функций, нужно алгебраическими преобразованиями выделить в числителе и в знаменателе критический множитель
делением целых многочленов или иррациональных функций, нужно алгебраическими преобразованиями выделить в числителе и в знаменателе критический множитель 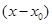 и сократить на него дробь.
и сократить на него дробь.
Правило 3. Чтобы раскрыть неопределенность 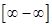 , нужно для выражения, стоящего под пределом, сделать алгебраические преобразования так, чтобы неопределенность исчезла или заменилась на неопределенность
, нужно для выражения, стоящего под пределом, сделать алгебраические преобразования так, чтобы неопределенность исчезла или заменилась на неопределенность 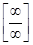 или
или 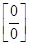 .
.
|
|
|
Правило 4. Неопределенность 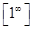 раскрывается сведением ко второму замечательному пределу:
раскрывается сведением ко второму замечательному пределу:  или
или  .
.
Правило 5. Для раскрытия неопределенности 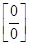 , образованной трансцендентными функциями (тригонометрическими, логарифмическими, показательными) или иррациональной функцией, нужно заменять бесконечно малые трансцендентные или иррациональные функции на эквивалентные им бесконечно малые алгебраические функции, используя следующие теоретические эквивалентности:
, образованной трансцендентными функциями (тригонометрическими, логарифмическими, показательными) или иррациональной функцией, нужно заменять бесконечно малые трансцендентные или иррациональные функции на эквивалентные им бесконечно малые алгебраические функции, используя следующие теоретические эквивалентности:
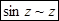 при
при 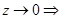
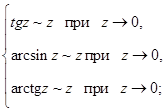
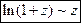
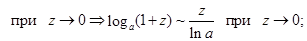
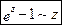
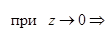
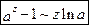
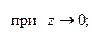
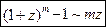
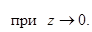
2. Принцип замены эквивалентных бесконечно малых:
При вычислении пределов любой бесконечно малый множитель можно заменить на ему эквивалентный, т.е. если при x → a имеем 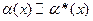 ,
, 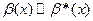 , то
, то
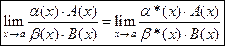 .
.
Аудиторные задания
Задача 1
Вычислите следующие пределы функции f (x), используя правила раскрытия основных неопределенностей; некоторые результаты проиллюстрируйте возможным локальным поведением графика функции f (x) в окрестности точки, в которой вычисляется предел; опишите смысл иллюстрации:
1)  ; 2)
; 2) 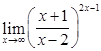 ; 3)
; 3)  ;
;
4) 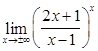 ; 5)
; 5)  ; 6)
; 6) 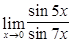 ;
;
7)  ; 8)
; 8) 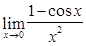 ; 9)
; 9) 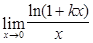 ;
;
10) 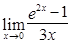 ; 11)
; 11)  ; 12)
; 12) 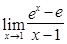 ;
;
13) 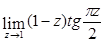 ; 14)
; 14) 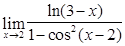 ; 15)
; 15)  ;
;
16) 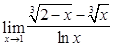 ; 17)
; 17)  ; 18)
; 18) 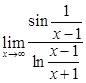 ;
;
19) 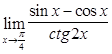 ; 20)
; 20) 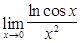 ; 21)
; 21)  .
.
Ответы: 1) 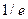 ; 2)
; 2) 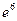 ; 3) e2; 4) + ∞, если x→+∞;0, если x→-∞; 5)
; 3) e2; 4) + ∞, если x→+∞;0, если x→-∞; 5) 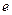 ; 6) 5/7; 7) 2/3;
; 6) 5/7; 7) 2/3;
8) 1/2; 9) k; 10) 2/3; 11) 1/2; 12) 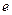
 ; 13)2/π; 14) ∞; 15) -3/20; 16) -2;
; 13)2/π; 14) ∞; 15) -3/20; 16) -2;
17) -4ln2; 18)-0,5; 19)  20)-0,5; 21) 0.
20)-0,5; 21) 0.
Задания для домашнего выполнения
Задача 1
Вычислите следующие пределы функции f (x), используя правила раскрытия основных неопределенностей; некоторые результаты проиллюстрируйте возможным локальным поведением графика функции f (x) в окрестности точки, в которой вычисляется предел; опишите смысл иллюстрации:
1)  ; 2)
; 2) 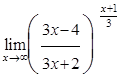 ; 3)
; 3) 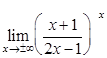 ;
;
4) 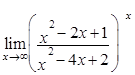 ; 5)
; 5) 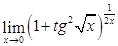 ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 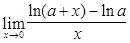 ; 9)
; 9)  ;
;
10) 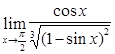 ; 11)
; 11) 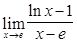 ; 12)
; 12) 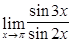 ;
;
13)  ; 14)
; 14) 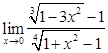 ; 15)
; 15) 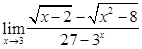 ;
;
16) 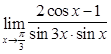 ; 17)
; 17) 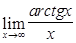 ; 18)
; 18) 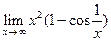 .
.
Ответы к заданиям для домашнего выполнения
Задача 1
|
|
|
1) 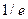 ; 2)
; 2) 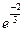 ; 3) 0, если x→+∞; +∞, если x→-∞; 4)
; 3) 0, если x→+∞; +∞, если x→-∞; 4) 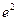 ; 5)
; 5) 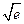 ;
;
6) 2/5; 7) 3/4; 8) 1/ a; 9) 1; 10) ∞; 11) 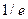 ; 12) -3/2;
; 12) -3/2;
13)2; 14) - 4; 15) 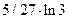 ; 16) 2/3; 17) 0; 18) 0,5;
; 16) 2/3; 17) 0; 18) 0,5;
Занятие 7. Самостоятельная работа «Пределы функций»
Цель занятия:
провести промежуточный контроль по технике вычисления различных пределов.
Самостоятельная работа «Пределы функций», вариант 0
Задача 1 (15 баллов)
Вычислите следующие пределы 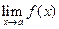 ; не менее чем в пяти задачах результат проиллюстрируйте графически локальным поведением функции f (x) в окрестности точки х = а и опишите смысл иллюстрации:
; не менее чем в пяти задачах результат проиллюстрируйте графически локальным поведением функции f (x) в окрестности точки х = а и опишите смысл иллюстрации:
1) 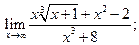 2)
2) 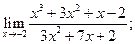 3)
3) 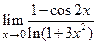 ;
;
4) 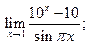 5)
5) 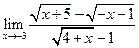 ; 6)
; 6) 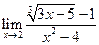 ;
;
7) 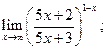 8)
8) 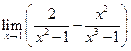 ; 9)
; 9) 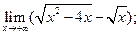 10)
10)  .
.
Задача 2(10 баллов)
Ответьте на вопросы о предельном поведении функции y = f (x), заданной графически:

| 1) ООФ, ОЗФ;
2) 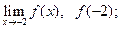 3)
3) 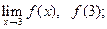 4)
4) 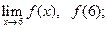 5)
5)  6)
6) 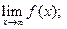 7)
7) 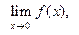 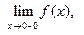 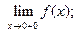 8)
8)  ; ;
|
9) укажите все точки, в окрестности которых f (x) является бесконечно малой;
10) укажите все точки, в окрестности которых f (x) является бесконечно большой.
Ответы к варианту 0 самостоятельной работы «Пределы функций»
Задача 1(15 баллов)
1) 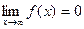 , где
, где 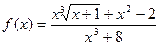 ;
;

| для значений x, достаточно больших по модулю, значения функции  становятся сколь угодно близкими к числу 0; становятся сколь угодно близкими к числу 0;
|
2) 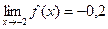 , где
, где 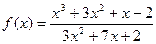 ;
;
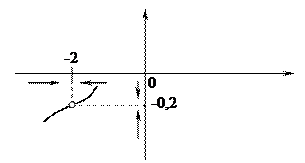
| точка x =-2 не входит в ООФ  , но окрестность этой точки входит в ООФ и значения функции , но окрестность этой точки входит в ООФ и значения функции  становятся сколь угодно близкими к числу -0,2, если брать значения аргумента я, достаточно близкими к числу -2; становятся сколь угодно близкими к числу -0,2, если брать значения аргумента я, достаточно близкими к числу -2;
|
3) 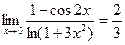 ; 4)
; 4)  ; 5)
; 5) 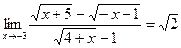 ;
;
6)  ; 7)
; 7)  ;
;
8)  , где
, где 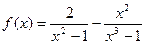 ;
;
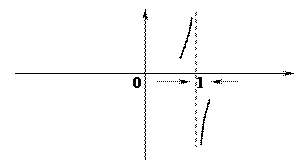
| точка x =1 не входит в ООФ  , но окрестность этой точки входит в ООФ и для значений x, достаточно близких к числу 1, значения функции , но окрестность этой точки входит в ООФ и для значений x, достаточно близких к числу 1, значения функции  становятся сколь угодно большими по модулю; становятся сколь угодно большими по модулю;
|
9) 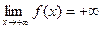 , где
, где 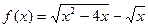 ;
;

| для достаточно больших положительных значений аргумента x функция  принимает сколь угодно большие положительные значения;
принимает сколь угодно большие положительные значения;
|
10) 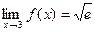 , где
, где  ;
;

| значения функции  становятся сколь угодно близкими к числу становятся сколь угодно близкими к числу 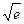 , если брать значения аргумента x,достаточно близкими к числу 3. , если брать значения аргумента x,достаточно близкими к числу 3.
|
Задача 2 (10 баллов)
1) ООФ: 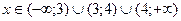 ;
;
ОЗФ:  ;
;
2) 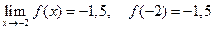 ;
;
3)  ;
;
4)  ;
;
5) 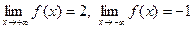 ;
;
6)  ;
;
7)  ;
;
8) 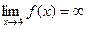 ;
;
9) f (x) является бесконечно малой в точках x =3 и x =6;
10) f (x) является бесконечно большой в точке x =4.
Занятие 8. Сравнение бесконечно малых
Цель занятия:
отработать процедуру сравнения бесконечно малых.
Краткие теоретические сведения
|
|
|
1. Сравнение бесконечно малых функций:
Чтобы сравнить две функции 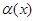 и
и  , являющиеся бесконечно малыми в окрестности одной и той же точки
, являющиеся бесконечно малыми в окрестности одной и той же точки  , нужно рассмотреть предел их отношения при
, нужно рассмотреть предел их отношения при  :
:
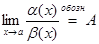 ;
;
по результату вычисления этого предела получаются следующие ответы:
1) если 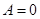 , то
, то 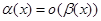 при
при  , т.е.
, т.е. 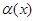 имеет более высокий порядок малости, чем б.м.
имеет более высокий порядок малости, чем б.м.  , при
, при  ;
;
2) если 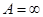 , то
, то  при
при  , т.е.
, т.е.  имеет более высокий порядок малости, чем
имеет более высокий порядок малости, чем 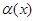 , или
, или 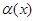 имеет более низкий порядок малости по сравнению с
имеет более низкий порядок малости по сравнению с  при
при  ;
;
3) если А – это число 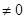 , то
, то  при
при  , т.е.
, т.е. 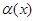 и
и  имеют одинаковый порядок малости при
имеют одинаковый порядок малости при  ;
;
в частности, если А =1, то 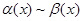 при
при  , т.е.
, т.е. 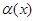 и
и  эквивалентны при
эквивалентны при  ;
;
4) если предел А не существует, то б.м. 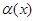 и
и  сравнить нельзя.
сравнить нельзя.
Таким образом, для решения задачи «сравнить две бесконечно малые функции» нужно вычислять предел отношения этих функций при  , где
, где  – это та точка, в которой обе сравниваемые функции являются бесконечно малыми.
– это та точка, в которой обе сравниваемые функции являются бесконечно малыми.
2. Порядок малости одной бесконечно малой функции относительно другой:
Число р называется порядком б.м. 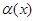 относительно б.м.
относительно б.м.  при
при  , если
, если 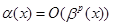 при
при  , т.е. если
, т.е. если 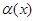 и
и 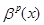 имеют одинаковый порядок малости при
имеют одинаковый порядок малости при  .
.
Из этого определения следует, что число p определяется из следующего условия:
 , где
, где 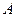 - число,
- число,  .
.
Аудиторные задания
Задача 1
Сравните две бесконечно малые величины:
1) 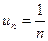 и
и 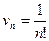 при
при  ;
;
2)  и
и 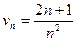 при
при  ;
;
3)  и
и 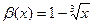 при
при  ;
;
4) 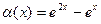 и
и  при
при  ;
;
5)  и
и 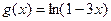 при
при  ;
;
6) 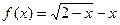 и
и  при
при  ;
;
Ответы:
1) 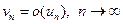 ; 2)
; 2) 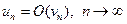 ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 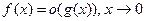 ; 6)
; 6) 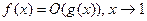 .
.
Задача 2
Определите порядок малости p относительно x функции f (x), которая является бесконечно малой при  :
:
1) 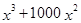 ; 2)
; 2) 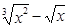 ; 3)
; 3) 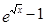 ; 4)
; 4) 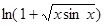 ; 5)
; 5) 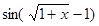 .
.
Ответы: 1) p =2; 2) p =1/2; 3) p =1/2; 4) p =3/2; 5) p =1.
|
|
|


