 |
Задания для домашнего выполнения
|
|
|
|
Задача 1
Вычислить следующие пределы последовательностей, используя основные теоремы о свойствах сходящихся последовательностей, бесконечно малых, бесконечно больших и ограниченных последовательностей; перечислите использованные свойства в каждом пределе.
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 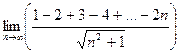 ; 9)
; 9)  ;
;
10)  ; 11)
; 11)  ; 12)
; 12)  .
.
Ответы к задачам для домашнего выполнения
Задача 1
1) 15/17; 2) 0; 3) 4; 4) 0; 5) 0; 6) 1; 7) 1/2;
8) -1; 9) 0; 10) -1,5; 11) 0; 12) 1.
Занятие 3. Самостоятельная работа «Предел последовательности»
Цель занятия:
проконтролировать усвоение знаний по основным понятиям пределов последовательностей.
Самостоятельная работа «Предел последовательности», вариант 0
Задача 1 (1балл)
Используя строгое определение предела последовательности, докажите, что 
Задача 2 (14 баллов)
Среди данных последовательностей  укажите номера а) сходящихся, б) расходящихся, в) бесконечно малых, г) бесконечно больших, д) ограниченных, е) монотонных последовательностей, записав предварительно каждую последовательность в развернутом виде и указав, чему равен
укажите номера а) сходящихся, б) расходящихся, в) бесконечно малых, г) бесконечно больших, д) ограниченных, е) монотонных последовательностей, записав предварительно каждую последовательность в развернутом виде и указав, чему равен  :
:
 ;
;
5)  ; 6)
; 6) 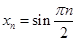 ; 7)
; 7)  ; 8)
; 8) 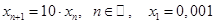 .
.
Задача 3 (2 балла)
Последовательность  задана рекуррентной формулой
задана рекуррентной формулой  ;
;
1) запишите члены этой последовательности и составьте формулу общего члена  ;
;
2) существует ли и чему равен  ? Приведите обоснование ответа.
? Приведите обоснование ответа.
Задача 4 (13 баллов)
а) Вычислите пределы последовательностей, используя свойства сходящихся, ограниченных, бесконечно малых и бесконечно больших последовательностей; поясните каждый ответ с точки зрения описательного определения предела последовательностей:
 ;
;
4)  ; 5)
; 5)  ;
;
б) сформулируйте теоремы, которые использовались при вычислении данных пределов.
|
|
|
Ответы к задачам 0 варианта сам. работы «Предел последовательности»
Задача 1 (1 балл)
 так как для
так как для 
Задача 2 (14 баллов)
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 

 .
.
а) сходящиеся последовательности: 2), 4), 5), 7);
б) расходящиеся последовательности: 1), 3), 6), 8);
в) бесконечно малые последовательности: 2), 5), 7);
г) бесконечно большие последовательности: 1), 8);
д) ограниченные последовательности: 2), 4), 5), 6), 7), 8);
е) монотонные последовательности:  1), 4), 8);
1), 4), 8);  5).
5).
Задача 3 (2 балла)
1) 
2)  так как последовательность
так как последовательность  представлена суммой числа 3 и бесконечной малой последовательности
представлена суммой числа 3 и бесконечной малой последовательности  .
.
Задача 4 (13 баллов)
а) 1) 
этот ответ означает, что члены последовательности с общим членом  становятся сколь угодно близкими к числу
становятся сколь угодно близкими к числу  , если брать номера этих членов достаточно большими;
, если брать номера этих членов достаточно большими;
2) 
этот ответ означает, что члены последовательности с  при достаточно больших номерах n сколь угодно близко подходят к числу 0;
при достаточно больших номерах n сколь угодно близко подходят к числу 0;
3) 
этот ответ означает, что члены последовательности с общим членом  при достаточно больших номерах n становятся сколь угодно большими;
при достаточно больших номерах n становятся сколь угодно большими;
4)  ;
;
этот результат означает, что члены последовательности с общим членом  становятся сколь угодно близкими к числу 1, если брать их номера n достаточно большими;
становятся сколь угодно близкими к числу 1, если брать их номера n достаточно большими;
5)  ;
;
этот ответ означает, что члены последовательности с общим членом  при достаточно больших номерах n становятся сколь угодно большими по модулю, но отрицательными.
при достаточно больших номерах n становятся сколь угодно большими по модулю, но отрицательными.
б) При вычислении пределов 1) - 5) использовались следующие теоремы:
1)теоремы о конечных пределах:
если  и
и  , то
, то  ,
,  при
при  ;
;
2) теоремы о бесконечно малых, бесконечно больших и ограниченных последовательностях:

 ;
;
 ,если складываемые б.б. имеют одинаковый знак.
,если складываемые б.б. имеют одинаковый знак.
Занятие 4. Определения предела функции в точке 
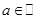 и при
и при  . Бесконечно малые, бесконечно большие и локально ограниченные функции. Чтение предельного поведения функции по её графику
. Бесконечно малые, бесконечно большие и локально ограниченные функции. Чтение предельного поведения функции по её графику
Цель занятия:
отработать основные понятия, связанные с предельным поведением функции непрерывного аргумента.
|
|
|
Краткие теоретические сведения
- Определение предела функции
 при
при  на языке последовательностей (по Гейне):
на языке последовательностей (по Гейне):

- Определение предела функции
 при
при  на языке окрестностей (по Коши):
на языке окрестностей (по Коши):

- Определения предела функции
 на языке «
на языке «  »:
»:
1) 
т.е.  , означает, что значения функции
, означает, что значения функции  становятся сколь угодно близкими к числу А, если брать значения аргумента x достаточно близкими к числу a;
становятся сколь угодно близкими к числу А, если брать значения аргумента x достаточно близкими к числу a;
2) 
т.е.  означает, что значения функции
означает, что значения функции  становятся сколь угодно большими по модулю, если брать значения аргумента x достаточно близкими к числу a;
становятся сколь угодно большими по модулю, если брать значения аргумента x достаточно близкими к числу a;
3) 
т.е.  означает, что значения функции
означает, что значения функции  становятся сколь угодно близкими к числу A, если брать значения аргумента x достаточно большими по модулю;
становятся сколь угодно близкими к числу A, если брать значения аргумента x достаточно большими по модулю;
4) 
т.е.  , означает, что значения функции
, означает, что значения функции  становятся сколь угодно большими по модулю, если брать значения аргумента x также достаточно большими по модулю.
становятся сколь угодно большими по модулю, если брать значения аргумента x также достаточно большими по модулю.
- Определение бесконечно малой (б.м.), бесконечно большой (б.б.) и локально ограниченной (лок. огр.) функции
 при
при  и некоторые связи между этими понятиями:
и некоторые связи между этими понятиями:
1)  – б.м. при
– б.м. при 
2)  – б.б. при
– б.б. при 
3)  – лок.огр. при
– лок.огр. при  в которой множество значений функции
в которой множество значений функции  является ограниченным;
является ограниченным;
4) если 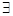 конечный
конечный  то функция
то функция  является локально ограниченной при
является локально ограниченной при 
5) если  , то функция
, то функция  является бесконечно большой при
является бесконечно большой при 
6) существование конечного предела функции  при
при  равносильно представлению этой функции в виде суммы этого предела и бесконечно малой функции при
равносильно представлению этой функции в виде суммы этого предела и бесконечно малой функции при  :
:

 где
где  – это б.м. функция при
– это б.м. функция при 
5. Односторонние пределы и их связь с пределом функции:
1) левосторонний предел: 
правосторонний предел: 
2) 
3) 
Аудиторные задания
Задача 1
Используя определение предела функции на языке  докажите что:
докажите что:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  .
.
Задача 2

По графику функции  дайте ответы на вопросы о предельном поведении функции в окрестностях различных значений её аргумента:
дайте ответы на вопросы о предельном поведении функции в окрестностях различных значений её аргумента:
1) 

2) 

3) 


4) 


5) 

6) 

7) 

8) укажите точки  в окрестностях которых функция
в окрестностях которых функция  является бесконечно малой;
является бесконечно малой;
9) укажите точки  в окрестностях которых функция
в окрестностях которых функция  является бесконечно большой;
является бесконечно большой;
10) укажите точки, в окрестностях которых функция  является локально ограниченной.
является локально ограниченной.
Задача 3
Представьте функцию  , имеющую конечный предел в каждой из точек
, имеющую конечный предел в каждой из точек  , в виде суммы этого предела и функции
, в виде суммы этого предела и функции  , бесконечно малой при
, бесконечно малой при  :
:
|
|
|
1) 
2) 
3) 
Ответы:
1) если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
2) если  , то
, то  , где
, где  ,
, 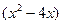 - б.м. при
- б.м. при  ;
;
если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
3) если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
если 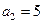 , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  .
.
Задания для домашнего выполнения
Задача 1
Используя определение предела функции на языке  , докажите что:
, докажите что:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 
Задача 2
По графику функции  ответить на вопросы о предельном поведении функции в окрестностях различных значений её аргумента:
ответить на вопросы о предельном поведении функции в окрестностях различных значений её аргумента:

1) 


2) 

3) 

4) 



5) 



6) 



7) 

8) укажите точки  в окрестностях которых функция
в окрестностях которых функция  является бесконечно малой;
является бесконечно малой;
9) укажите точки  в окрестностях которых функция
в окрестностях которых функция  является бесконечно большой.
является бесконечно большой.
10) укажите точки, в окрестностях которых функция  является локально ограниченной.
является локально ограниченной.
Задача 3
Представьте функцию  , имеющую конечный предел в каждой из точек
, имеющую конечный предел в каждой из точек  , в виде суммы этого предела и функции
, в виде суммы этого предела и функции  , бесконечно малой при
, бесконечно малой при  :
:
1) 
2) 
3)  .
.
Ответы к заданиям для домашнего выполнения
Задача 3
1) если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
2) если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
3) если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  ;
;
если  , то
, то  , где
, где  ,
,  - б.м. при
- б.м. при  .
.
Занятие 5. Теоремы о функциях, имеющих конечные пределы, о бесконечно малых, бесконечно больших и локально ограниченных функциях. Раскрытие основных неопределенностей, образованных алгебраическими функциями
Цель занятия:
1) использовать теоремы о конечных пределах функций, о бесконечно малых, бесконечно больших и локально ограниченных функциях для практического вычисления пределов;
2) рассмотреть приемы раскрытия неопределенностей  ,
,  ,
,  , образованных алгебраическими функциями.
, образованных алгебраическими функциями.
Краткие теоретические сведения
- Основные теоремы о функциях, имеющих конечные пределы:
1) если  непрерывна в точке
непрерывна в точке  , то
, то  ;
;
2)  ;
;
3)  , где C-const по x;
, где C-const по x;
4) если  и
и  ,
, 
то 
- Основные теоремы о бесконечно малых функциях:
 ;
;  ;
;  ;
;
 , если лок.огр. не является б.м.
, если лок.огр. не является б.м.
- Основные теоремы о бесконечно больших функциях:
 ;
;  ;
;
|
|
|
 , если лок.огр. не является б.м.;
, если лок.огр. не является б.м.;

Аудиторные задания
Задача 1
Вычислите пределы функций f (x), используя теоремы о функциях, имеющих конечные пределы, о бесконечно малых, бесконечно больших и локально ограниченных функциях; результат вычисления проиллюстрируйте возможным локальным поведением графика функции f (x) в окрестности той точки, в которой вычисляется предел; опишите словами смысл иллюстрации:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ; 9)
; 9)  ;
;
10)  ; 11)
; 11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  .
.
Ответы: 1) 9; 2) ∞; 3) 0; 4) -0,4; 5) 0; 6) 0,5; 7) 0; 8) -1; 9) 0; 10) 4;
11) 2/3; 12) 0; 13) 0, если x→+∞; +∞, если x→-∞; 14) 1/13.
|
|
|


