 |
Задания для домашнего выполнения
|
|
|
|
Задача 1
Сравните две бесконечно малые величины:
1)  и
и  при
при  ;
;
2)  и
и  при
при  ;
;
3)  и
и  при
при 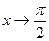 ;
;
4)  и
и  при
при 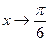 ;
;
5)  и
и  при
при  ;
;
Задача 2
Определите порядок малости p относительно x функции f (x), которая является бесконечно малой при  :
:
1) 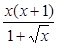 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 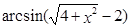 .
.
Ответы к заданиям для домашнего выполнения
Задача 1
1) 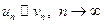 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 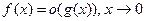 .
.
Задача 2
1) p =1; 2) p =10; 3) p =1; 4) p =1; 5) p =2.
Занятие 9. Исследование функций на непрерывность
Цель занятия:
1) отработать основные определения, связанные с непрерывностью функции в точке;
2) научиться описывать по графику свойство непрерывности функций.
Краткая теоретическая справка
1. Определение непрерывности функции в точке:
Функция 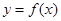 называется непрерывной в точке x 0, если выполняются следующие условия:
называется непрерывной в точке x 0, если выполняются следующие условия:
1) точка  вместе с некоторой своей окрестностью;
вместе с некоторой своей окрестностью;
2) 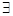 конечный
конечный 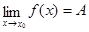 ;
;
3)  , т.е. этот предел совпадает со значением функции в точке
, т.е. этот предел совпадает со значением функции в точке  .
.
Если функция 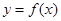 непрерывна в точке
непрерывна в точке  , то это означает, что её график проходит через точку
, то это означает, что её график проходит через точку  , не прерываясь.
, не прерываясь.
2. Определение точки разрыва:
Точка  называется точкой разрыва функции
называется точкой разрыва функции 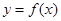 , если функция определена в окрестности этой точки (за исключением, быть может, самой точки
, если функция определена в окрестности этой точки (за исключением, быть может, самой точки  ), но не является в ней непрерывной, (т.е. не выполняется хотя бы одно из требований определения непрерывности).
), но не является в ней непрерывной, (т.е. не выполняется хотя бы одно из требований определения непрерывности).
3. Типы точек разрыва:
1) разрыв типа выколотой точки, или устранимый разрыв в точке  , если существует конечный предел
, если существует конечный предел  , но этот предел не совпадает со значением функции f (x 0):
, но этот предел не совпадает со значением функции f (x 0):

|

|
2) разрыв типа скачка в точке x 0, если не существует конечный предел 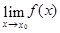 , но существуют конечные односторонние пределы этой функции в точке x 0:
, но существуют конечные односторонние пределы этой функции в точке x 0:

|

|
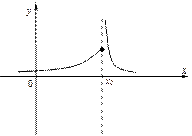
3) бесконечный разрыв в точке x 0, если не существует конечный предел 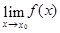 , но при этом хотя бы один из односторонних пределов
, но при этом хотя бы один из односторонних пределов  является бесконечным:
является бесконечным:
|
|
|

| 
| 
|
4. Классификация точек разрыва:
1) точки разрыва I рода, или точки конечного разрыва – это точки разрыва типа выколотой точки или типа скачка;
2) точки разрыва II рода – это точки бесконечного разрыва и точки разрыва, которые характеризуются тем, что хотя бы один из односторонних пределов  не существует.
не существует.
5. Основные свойства функций, непрерывных в точке:
1) если две функции  и
и  непрерывны в точке
непрерывны в точке  , то непрерывными в этой же точке являются их сумма
, то непрерывными в этой же точке являются их сумма  , их произведение
, их произведение  , а также их отношение
, а также их отношение  , но при условии, что
, но при условии, что 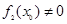 ;
;
2) если функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , то суперпозиция этих функций
, то суперпозиция этих функций  является непрерывной в точке
является непрерывной в точке  ;
;
3) каждая из основных элементарных функций (степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические, гиперболические) является непрерывной в каждой точке своей ООФ;
4) любая элементарная функция (получается из основных элементарных функций конечным числом арифметических операций и суперпозиций) является непрерывной в каждой точке своей ООФ.
6. Определение функции, непрерывной на промежутке:
Функция 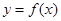 называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка;
называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка;
в случае, когда промежуток является конечным и замкнутым, т.е.  , то на его концах
, то на его концах  и
и  требуется односторонняя непрерывность (правосторонняя в точке
требуется односторонняя непрерывность (правосторонняя в точке  и левосторонняя в точке
и левосторонняя в точке  ).
).
7. Исследовать заданную функцию  на непрерывность – это означает:
на непрерывность – это означает:
1) описать множество всех точек x, в которых функция является непрерывной;
2) перечислить точки разрывов и указать тип каждого разрыва;
3) построить график функции (полностью или в окрестности каждой точки разрыва).
Аудиторные задания
Задача 1
Постройте график кусочно-заданной функции и по графику опишите свойство непрерывности этой функции; сформулируйте при этом рабочие определения:
|
|
|
1)  2)
2)  .
.
Ответы:
1)
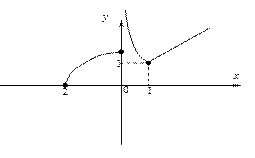
| Функция y = f (x) является непрерывной при  и при и при  , при этом в точке x =-2 непрерывность является односторонней; x =0 – точка разрыва, т.к. не , при этом в точке x =-2 непрерывность является односторонней; x =0 – точка разрыва, т.к. не   , тип разрыва в точке x =0 бесконечный, т.к. один из односторонних пределов f (x) при x →0 является бесконечным. , тип разрыва в точке x =0 бесконечный, т.к. один из односторонних пределов f (x) при x →0 является бесконечным.
|
2)

| Функция y = f (x) является непрерывной при  , при , при  , при , при  и при и при 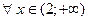 ; имеет 3 точки разрыва x =0, x =1, x =2, т.к. в каждой из этих точек не выполняется определение непрерывности функции; типы точек разрывов:
x = 0 - бесконечный разрыв, т.к. ; имеет 3 точки разрыва x =0, x =1, x =2, т.к. в каждой из этих точек не выполняется определение непрерывности функции; типы точек разрывов:
x = 0 - бесконечный разрыв, т.к.  ;
x = 1 – разрыв типа выколотой точки, т.к. ;
x = 1 – разрыв типа выколотой точки, т.к.  ;
x = 2 – разрыв типа скачка, т.к., ;
x = 2 – разрыв типа скачка, т.к., 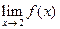 не, не,  но есть конечные односторонние пределы но есть конечные односторонние пределы  и и 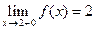 . .
|
Задача 2
Исследуйте непрерывность элементарной функции, используя основные свойства непрерывных функций; построите часть графика функции в окрестности каждой точки разрыва:
1)  ; 2)
; 2)  .
.
Ответы:
1)
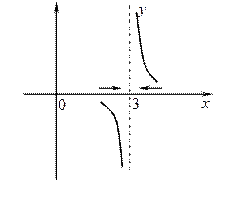
| Функция  является непрерывной при является непрерывной при  и при и при  , т.к. данная функция относится к элементарным функциям, следовательно, является непрерывной в каждой точке , т.к. данная функция относится к элементарным функциям, следовательно, является непрерывной в каждой точке  ;
x = 3 – точка разрыва, т.к. не принадлежит ООФ, но её окрестность входит в ООФ; тип разрыва – бесконечный, т.к. ;
x = 3 – точка разрыва, т.к. не принадлежит ООФ, но её окрестность входит в ООФ; тип разрыва – бесконечный, т.к.
 , ,  . .
|
2)

| Функция  является непрерывной при является непрерывной при  и при и при 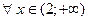 , т.к. данная функция относится к элементарным функциям, следовательно, является непрерывной в каждой точке , т.к. данная функция относится к элементарным функциям, следовательно, является непрерывной в каждой точке  ;
x = 2 – точка разрыва, т.к. не принадлежит ООФ, но её окрестность входит в ООФ; тип разрыва – бесконечный, т.к. ;
x = 2 – точка разрыва, т.к. не принадлежит ООФ, но её окрестность входит в ООФ; тип разрыва – бесконечный, т.к. 
|
|
|
|


