 |
Принцип Гамильтона (наименьшего действия). Уравнения движения
|
|
|
|

|
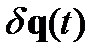
|
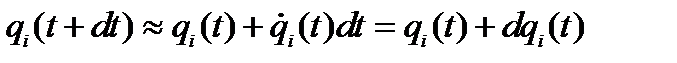
Пусть 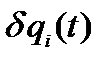 - вариация координаты (произвольное изменение координаты в данный момент времени). Будем рассматривать бесконечно малые
- вариация координаты (произвольное изменение координаты в данный момент времени). Будем рассматривать бесконечно малые  , следовательно, 2-я возможная траектория будет в непосредственной близости от 1-ой. Возможная траектория – траектория, которая может получиться при данных взаимодействиях. Возможных траекторий много, реальных – одна. В начальной и конечной точке траектории вариации координат равны нулю:
, следовательно, 2-я возможная траектория будет в непосредственной близости от 1-ой. Возможная траектория – траектория, которая может получиться при данных взаимодействиях. Возможных траекторий много, реальных – одна. В начальной и конечной точке траектории вариации координат равны нулю:
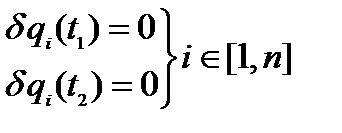
 , т.е.
, т.е. 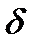 и
и 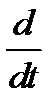 коммутативны:
коммутативны:
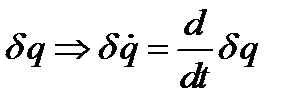
Будем искать первую вариацию 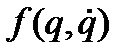 (линейную вариацию по вариацию аргумента).
(линейную вариацию по вариацию аргумента).
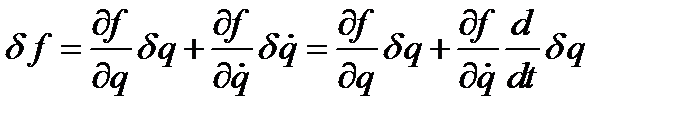
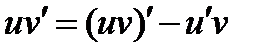
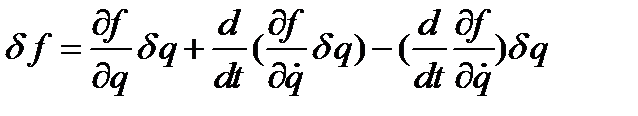
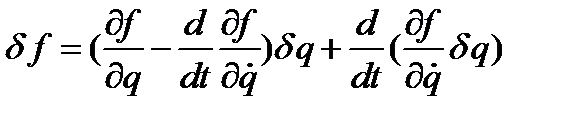
Введём функционал:
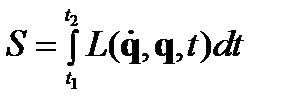
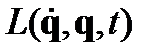 - функция Лагранжа, функция динамических переменных и времени.
- функция Лагранжа, функция динамических переменных и времени.
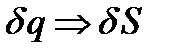
Принцип наименьшего действия:
Из всех возможных траекторий, между данными точками, механической системы в конфигурационном пространстве реализуется та, для которой первая вариация действия равна нулю:
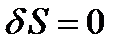

Найдём 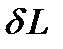 :
:

Тогда:
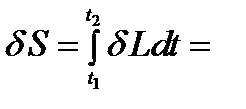
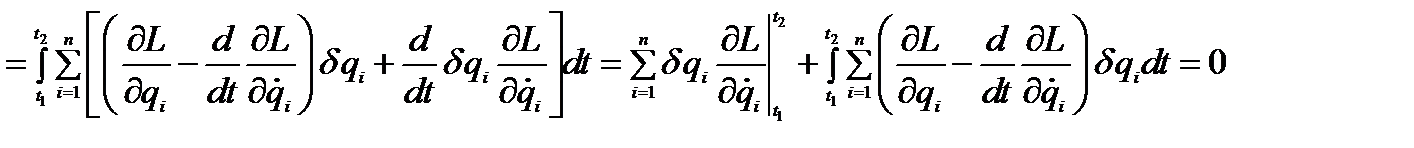
Первое слагаемое в правой части данного выражения равно нулю, тогда остаётся:

Координаты  независимы, вариации этих координат так же независимы. Условие независимости
независимы, вариации этих координат так же независимы. Условие независимости 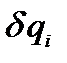 означает, что все коэффициенты при
означает, что все коэффициенты при 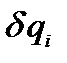 равны нулю. В результате получаем:
равны нулю. В результате получаем:
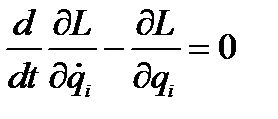 ,
, 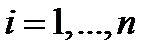
Мы получили уравнения движения Лагранжа. Это дифференциальные уравнения второго порядка, что бы их решить, нужны начальные условия: 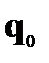 и
и 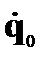 . В результате получим закон движения
. В результате получим закон движения 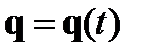
Функция Лагранжа и её свойства. Правило суммирования Эйнштейна. Функция Лагранжа простейших систем.
Каждой системе ставится в соответствие функция динамических переменных  , называемая функцией Лагранжа.
, называемая функцией Лагранжа.
Свойства:
1. Уравнение движения Лагранжа инвариантно относительно следующего преобразования:
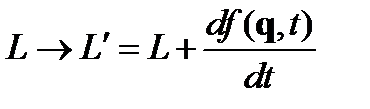
Надо доказать, что  .
.

Рассмотрим вариацию 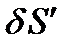 :
:
|
|
|
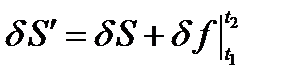
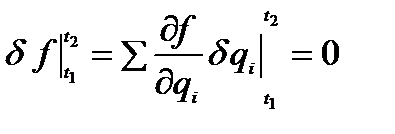 (вариации координат на концах траектории равны нулю).
(вариации координат на концах траектории равны нулю).
Итак, вывод: функция Лагранжа может быть задана с точностью до полной производной по времени функции обобщённых координат и времени. Это не влияет на уравнения движения, а следовательно на решение задачи.
2. Энергии(T и U)
a) 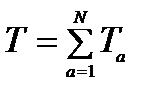 (N- число материальных точек)
(N- число материальных точек)
Т – кинетическая энергия, величина аддитивная.
б) 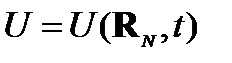
U – потенциальная энергия не аддитивна.
(U – аддитивна, когда нет взаимодействия между точками системы).
Правило суммирования Эйнштейна
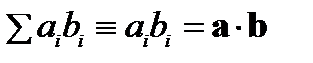
Знак суммы не пишется при дважды встречающемся индексе.
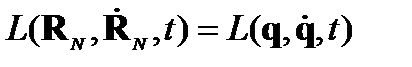
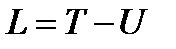 ,
, 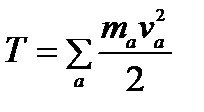
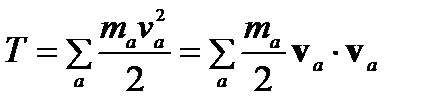

тогда:
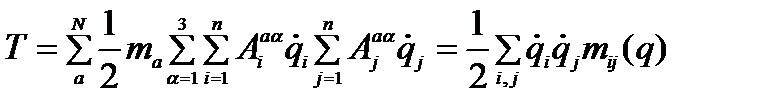 - для стационарных связей
- для стационарных связей
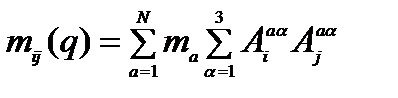
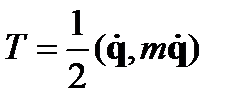 - однородная функция своих переменных
- однородная функция своих переменных 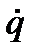 , у неё второй порядок, т.е.:
, у неё второй порядок, т.е.:
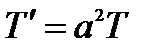
Соотношение Эйлера для однородной функции:
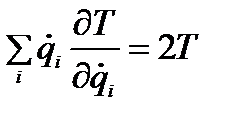
Функции Лагранжа простейших систем
Рассмотрим системы с одной степенью свободы. 
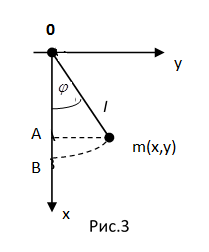
1. Плоский математический маятник (Рис.3).
 - уравнение связи.
- уравнение связи.
Число степеней свободы равно единице (см. §1).
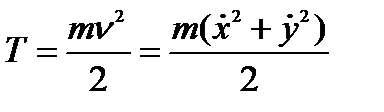 - кинетическая энергия.
- кинетическая энергия.

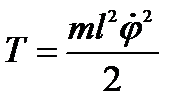
U – потенциальная энергия.
U=mgh, где h – уровень подъёма над положением равновесия.
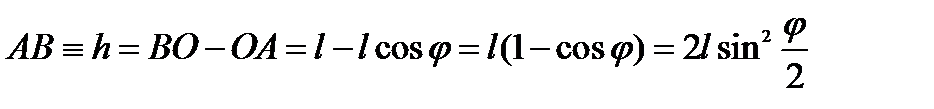
Имеем:
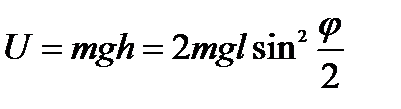
Рассмотрим случай малых колебаний:
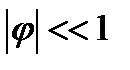 , φ – измеряется в радианах.
, φ – измеряется в радианах.
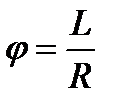
L – длина дуги, R – радиус окружности. Тогда:

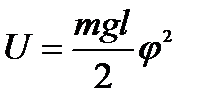
Функция Лагранжа:

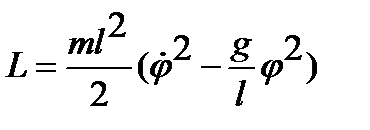
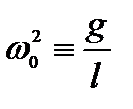
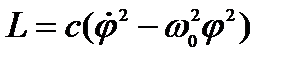
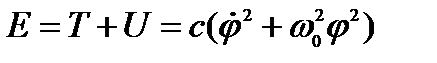
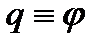
Уравнение движения:
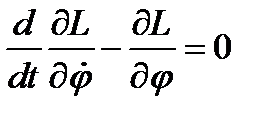
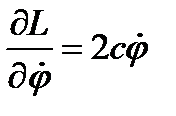
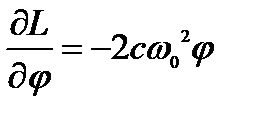
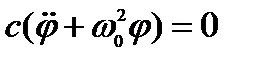

Для решения дифференциального уравнения второго порядка необходимо два начальных условия:
1) 
2) 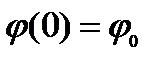
2. Линейный гармонический осциллятор (Рис.4).
k – упругость пружины,
| m |
| k, l0,l |
| Рис.4 Линейный гармонический осциллятор |
l – длина пружины в деформированном состоянии.
По закону Гука (для малых деформаций):


 - малые деформации.
- малые деформации.
По второму закону Ньютона:
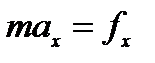 ,
, 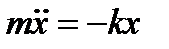
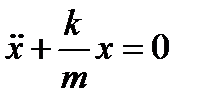 ,
, 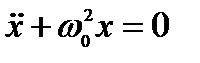 , где
, где 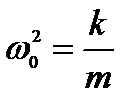 .
.
Решение аналогично случаю 1. Начальные условия:
| x |
| m |
| l0 |
| l1 |
| Dl0 |
| Рис.5 Вертикальный гармонический осциллятор |
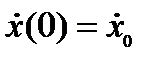
2) 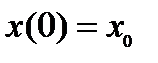
3. Аналогично для вертикального гармонического осциллятора (Рис.5)
|
|
|
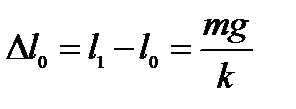 (По закону Гука)
(По закону Гука)
В данном случае: 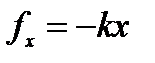 - не является результирующей силой, а лишь возвращающей систему к положению равновесия.
- не является результирующей силой, а лишь возвращающей систему к положению равновесия.
|
|
|


