 |
Статистическое описание систем с большим числом степеней свободы. Метод статистической физики (элементы теории вероятностей). Микро- и макро- параметры системы
|
|
|
|
Статистическая физика изучает системы с большим числом степеней свободы. Наличие большого число степеней свободы вносит некоторые особенности в описание таких систем. Например, в 1 см  воздуха содержится
воздуха содержится  частиц (число Лошмидта), но у каждой материальной точки (частицы) имеется 3 степени свободы, поэтому у этой системы огромное число степеней свободы.
частиц (число Лошмидта), но у каждой материальной точки (частицы) имеется 3 степени свободы, поэтому у этой системы огромное число степеней свободы.
В классической механике возможно описывать такие системы (через формализм Гамильтона) –  динамических переменных
динамических переменных  , где
, где  – число степеней свободы. Описание системы сводится к решению уравнений:
– число степеней свободы. Описание системы сводится к решению уравнений:

Чтобы решить данную систему, необходимо задать  начальных условий. Задаем начальные условия и решаем систему. Но здесь сложные технические трудности (долгий счёт на ЭВМ). Но имеются ещё и качественные особенности этих систем, которые не охватываются этими уравнениями, то есть детерминированный подход здесь не используют.
начальных условий. Задаем начальные условия и решаем систему. Но здесь сложные технические трудности (долгий счёт на ЭВМ). Но имеются ещё и качественные особенности этих систем, которые не охватываются этими уравнениями, то есть детерминированный подход здесь не используют.
Статистическая физика рассматривает переход от малого числа степеней свободы к большому.  и
и 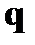 – это динамические переменные. Фазовое пространство – это
– это динамические переменные. Фазовое пространство – это  -мерное пространство, декартовыми осями которого являются переменные
-мерное пространство, декартовыми осями которого являются переменные  и
и  . Тогда состояние системы (которое задаётся динамическими переменными) в фазовом пространстве задаётся фазовой точкой. Движение системы в реальном пространстве задаётся движением фазовой точки в фазовом пространстве, то есть устанавливается соответствие между фазовым и реальным пространствами.
. Тогда состояние системы (которое задаётся динамическими переменными) в фазовом пространстве задаётся фазовой точкой. Движение системы в реальном пространстве задаётся движением фазовой точки в фазовом пространстве, то есть устанавливается соответствие между фазовым и реальным пространствами.
Основной метод статистической физики – теория вероятностей. В теории вероятностей для описания событий задаётся, или вводится, вероятность:
 – поле событий,
– поле событий,  – вероятность, тогда:
– вероятность, тогда:
 .
.
При изучении конкретных систем, для измерения вероятностей используется закон больших чисел, который разработал Чебышёв. На основе закона больших чисел вводится аксиома измерений вероятностей (в абстрактной теории закона измерения нет), через частоту появления события и через предельные соотношения.
|
|
|
Далее в теории вероятностей вводится либо дискретное, либо непрерывное множество.
На ряду с  вводится
вводится 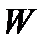 :
: 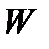 – вероятность того, что некоторая величина заключена в интервале
– вероятность того, что некоторая величина заключена в интервале  :
:
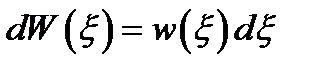 ,
,  .
.
Здесь  – плотность вероятности. Плотность вероятности вводится для непрерывных объектов, случайных процессов и полей, которые сплошь заполняют исследуемые множества.
– плотность вероятности. Плотность вероятности вводится для непрерывных объектов, случайных процессов и полей, которые сплошь заполняют исследуемые множества.
Под  понимается
понимается  в момент времени
в момент времени 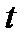 :
:  .
.
Запишем  -точечную функцию распределения (или плотность распределения):
-точечную функцию распределения (или плотность распределения):
 ,
,
здесь  ,
,  .
.
Функции  обладают определённым набором свойств:
обладают определённым набором свойств:
1) Неотрицательность;
2) Симметричность, то есть инвариантность относительно перестановок:
 ;
;
3) Согласованность, то есть после интегрирования  получаем:
получаем:
 ;
;
4) Нормированность на единицу:
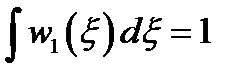 .
.
Каждое состояние системы описывается набором динамических переменныx  и
и  . В ансамблях таких систем, из большого числа параметров, которые можно построить на переменных
. В ансамблях таких систем, из большого числа параметров, которые можно построить на переменных  и
и  , можно выделить небольшое число параметров, которые являются наиболее важными для описания системы.
, можно выделить небольшое число параметров, которые являются наиболее важными для описания системы.
Введём такой параметр:
 .
.
Выясняется, что эта величина в зависимости от  может принимать различные значения, то есть является функцией от
может принимать различные значения, то есть является функцией от  . Параметр, определяемый динамическими переменными, называется микропараметром. Наряду с этой величиной вводится параметр аналогичный, который определяется в более длительный момент времени и характеризует систему в целом – макропараметр.
. Параметр, определяемый динамическими переменными, называется микропараметром. Наряду с этой величиной вводится параметр аналогичный, который определяется в более длительный момент времени и характеризует систему в целом – макропараметр.
Будем рассматривать в этом курсе стационарные явления или стационарные системы – системы, свойства которых не зависят от времени. То есть, если рассмотреть ось  , то для стационарных сред начало наблюдения за системой можно выбрать в любой точке оси
, то для стационарных сред начало наблюдения за системой можно выбрать в любой точке оси  :
:
|
|
|

|
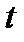
|

И для таких процессов начальные условия динамических переменных не оказывают влияние на результат, то есть начальные условия могут быть отброшены, так как часы пускаем в любой момент времени.
Итак, в стационарных системах:
1) Время начала отсчёта  можно перемещать по оси времени;
можно перемещать по оси времени;
2) Начальные условия отбрасываются;
3) Граничные условия, оказывается, не влияют на систему (если система стационарная).
Через границу вешнее воздействие проникает и через некоторое время действует на систему. Действие идёт через точки, находящиеся в очень узком приграничном слое. Так как количество этих точек мало, по сравнению с точками системы, то граничные условия можно не учитывать. Это обстоятельство можно использовать при рассмотрении двух подсистем. Взаимодействие подсистем в достаточно малом промежутке времени не оказывает влияние на подсистемы, так как на границе точек пренебрежимо мало по сравнению с подсистемами.
Выясняется, что микро и макро параметры  , если наблюдать за ними в течение большого промежутка времени, то в большей части этого промежутка времени, система обладает конкретными или близкими к нему параметрами. Если усреднить этот параметр, то он не будет отличаться от конкретного параметра.
, если наблюдать за ними в течение большого промежутка времени, то в большей части этого промежутка времени, система обладает конкретными или близкими к нему параметрами. Если усреднить этот параметр, то он не будет отличаться от конкретного параметра.
В качестве результата наблюдения  , принимается значение среднего по времени от
, принимается значение среднего по времени от  :
:
 .
.
Если 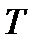 – время наблюдения, то выражение, стоящее в скобках верно, но так как
– время наблюдения, то выражение, стоящее в скобках верно, но так как  очень велико, то пишут предел. Это и предлагают воспринимать как наблюдаемую величину (в теории).
очень велико, то пишут предел. Это и предлагают воспринимать как наблюдаемую величину (в теории).
|
|
|


