 |
Задачи по курсу «Теоретическая физика»
|
|
|
|
 1. Наити функцию Лагранжа двойного плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g). 1. Наити функцию Лагранжа двойного плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g).
|
 2.Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m2, точка которого (с массой m1 в ней) может совершать движения по горизонтальной прямой. 2.Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m2, точка которого (с массой m1 в ней) может совершать движения по горизонтальной прямой.
|
| 3.Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах. |
| 4.Выразить амплитуду xm и начальную фазу φ0 колебаний x=x(t) через начальные значения x0, v0 координаты и скорости. |
 5.Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F. 5.Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F.
|
 6.Найти частоту колебаний изображенного на рисунке 4 маятника, точка подвеса которого (с массой m1 в ней) способна совершать движение в горизонтальном направлении. 6.Найти частоту колебаний изображенного на рисунке 4 маятника, точка подвеса которого (с массой m1 в ней) способна совершать движение в горизонтальном направлении.
|
7.  Определить малые колебания двойного плоского маятника. Определить малые колебания двойного плоского маятника.
|
8.Рассмотреть следующие операторы на предмет линейности  :
5) инверсии :
5) инверсии 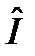 : :  ;
6) трансляции ;
6) трансляции  : :  ;
7) изменения масштаба ;
7) изменения масштаба  : :  ;
8) комплексного сопряжения ;
8) комплексного сопряжения  : :  . .
|
9.Используя свойства:
4)  ,
5) ,
5)  ,
6) ,
6)  скалярного произведения скалярного произведения
 , , 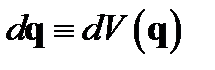 .
Доказать неравенство Коши-Шварца-Буняковского .
Доказать неравенство Коши-Шварца-Буняковского
 . .
|
10.Найти оператор  , если
3) , если
3) 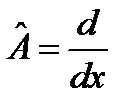 , , 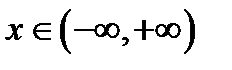 , ,  , ,  ;
4) ;
4)  , ,  , ,  , , 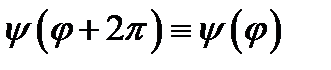 ; ;
|
11.Показать, что произвольный линейный оператор  может быть представлен в виде может быть представлен в виде  , ,  , ,  . .
|
12.. Найти  , если , если 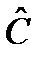 – произведение эрмитовых операторов – произведение эрмитовых операторов  и и  . .
|
13.Показать, что при условии эрмитовости 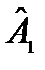 и и  операторы операторы  и и 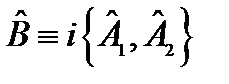 , также эрмитовы. , также эрмитовы.
|
14.Используя определение 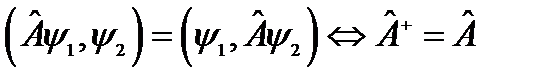 и свойство и свойство  , показать, что уравнение , показать, что уравнение  имеет решение лишь для вещественного числа имеет решение лишь для вещественного числа  . .
|
15.Доказать, что собственные функции эрмитова оператора  с невырожденным дискретным спектром ортогональны. с невырожденным дискретным спектром ортогональны.
|
16.Используя свойство ортонормированности, найти коэффициенты  разложения произвольной функции разложения произвольной функции  по базису в гильбертовом пространстве. по базису в гильбертовом пространстве.
|
17.Решить уравнение (14.3) для оператора  , ,  . .
|
18.Решить уравнение (14.3) для оператора  , ,  . .
|
19.Для стационарного состояния вида
 (19.1)
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины (19.1)
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины  , рассчитать средние значения величин, соответствующих операторам:
3) , рассчитать средние значения величин, соответствующих операторам:
3)  ;
4) ;
4)  . .
|
20.В 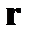 -представлении получить явный вид оператора -представлении получить явный вид оператора 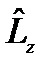 , используя координаты
3) декартовы;
4) сферические. , используя координаты
3) декартовы;
4) сферические.
|
21.Математический маятник совершает гармонические колебания по закону   . Найти вероятность того, что при случайном измерении отклонения . Найти вероятность того, что при случайном измерении отклонения  маятника это значение будет лежать в интервале маятника это значение будет лежать в интервале  . .
|
22.Вероятность того, что  и и 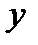 лежат в интервалах: лежат в интервалах:  и и 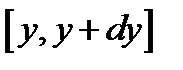 дается выражением: дается выражением:  , ,  . Считая, что областями измерения переменных . Считая, что областями измерения переменных  и и  являются являются  и и  , найти константу нормировки , найти константу нормировки  . .
|
23.Определить вероятность того, что значение величины  будет лежать в интервале будет лежать в интервале 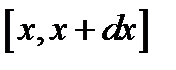 . .  , ,  . .
|
|
|
|
Вопросы по курсу «Теоретическая физика».
1. Обобщенные координаты. Понятие числа степеней свободы. Описание эволюции системы в конфигурационном пространстве.
2. Принцип наименьшего действия. Уравнение движения.
3. Функция Лагранжа и ее свойства. Правило суммирования Эйнштейна. Функция Лагранжа простейших систем.
4. Интегралы движения (метод Лагранжа). Свойства симметрии пространства и времени. Законы сохранения.
5. Обобщенный импульс. Преобразование Лежандра. Уравнения Гамильтона. Канонически сопряженные величины.
6. Функция Гамильтона и ее свойства. Функции Гамильтона простейших систем.
7. Малые колебания. Свойства потенциальной энергии.
8. Принцип неопределенности. Полный набор динамических переменных. Постулаты квантовой механики.
|
|
|
9. Волновая функция и ее свойства. Принцип суперпозиции состояний.
10. Операторы в квантовой механике и их свойства.
11. Собственные функции и собственные значения эрмитовых операторов и их свойства. Случай дискретного спектра.
12. Операторы координаты 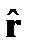 , импульса
, импульса 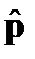 , момента импульса
, момента импульса  , энергии
, энергии  и их свойства.
и их свойства.
13. Волновое уравнение.
14. Стационарные состояния различных систем.
15. Решение волнового уравнения в случае свободной материальной точки.
16. Собственный механический момент (спин). Спиновая переменная волновой функции. Нормировка функций.
17. Принцип тождественности. Оператор перестановки и его свойства.
18. Статистическое описание систем с большим числом степеней свободы. Метод статистической физики (элементы теории вероятностей).
19. Распределение Ферми-Дирака.
20. Распределение Бозе-Эйнштейна.
Вопросы по курсу «Теоретическая физика»
(план минимум)
1. Обобщенные координаты. Функция Лагранжа простейших систем.
2. Принцип наименьшего действия. Уравнение движения.
3. Законы сохранения. Обобщенный импульс.
4. Функции Гамильтона простейших систем.
5. Принцип неопределенности. Полный набор динамических переменных. Постулаты квантовой механики.
6. Волновая функция и ее свойства. Принцип суперпозиции состояний.
7. Операторы в квантовой механике и их свойства.
8. Собственные функции и собственные значения эрмитовых операторов и их свойства. Случай дискретного спектра.
9. Операторы координаты 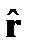 , импульса
, импульса 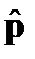 , момента импульса
, момента импульса  , энергии
, энергии  и их свойства.
и их свойства.
10. Волновое уравнение.
11. Стационарные состояния: случай свободной материальной точки.
12. Собственный механический момент (спин). Спиновая переменная волновой функции.
13. Статистическое описание систем с большим числом степеней свободы. Два способа усреднения в статистической физике.
14. Распределение Ферми-Дирака.
15. Распределение Бозе-Эйнштейна.
Задачи по курсу «Теоретическая физика»
(план минимум)
1. Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.
2. Найти оператор  , если
, если
1) 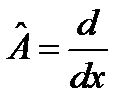 ,
,  ,
,  ,
,  ;
;
2) 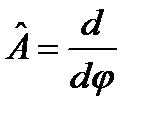 ,
, 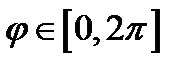 ,
, 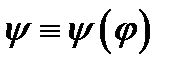 ,
,  .
.
3. Найти  , если
, если  – произведение эрмитовых операторов
– произведение эрмитовых операторов  и
и  . В сферических координатах
. В сферических координатах  -представления найти собственную функцию оператора
-представления найти собственную функцию оператора 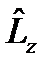 .
.
|
|
|
4. В  -представлении (одномерная система) решить уравнение
-представлении (одномерная система) решить уравнение  для оператора
для оператора  в случае частицы в бесконечно глубокой потенциальной яме, ширины
в случае частицы в бесконечно глубокой потенциальной яме, ширины  .
.
5. Вероятность того, что  и
и  лежат в интервалах:
лежат в интервалах:  и
и  дается выражением:
дается выражением:  ,
,  . Считая, что областями измерения переменных
. Считая, что областями измерения переменных  и
и  является
является  и
и  , найти константу нормировки
, найти константу нормировки  .
.
|
|
|


