 |
Задачи по курсу «Теоретическая физика» и их решение.
|
|
|
|
Задача 
1. Найти функцию Лагранжа двойного плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g).
Решение. В качестве координат берём углы φ1 и φ2, которые нити l1 и l2 образуют с вертикалью. Тогда для точки m1 имеем:
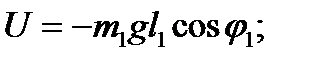
чтобы найти кинетическую энергию второй точки, выражаем её декартовы координаты x2, y2 (начало координат в точке подвеса, ось y – по вертикали вниз) через углы φ1 и φ2:
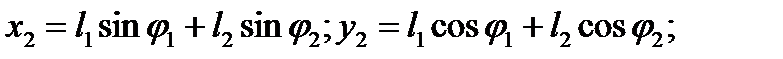
после этого получим:
окончательно:
Задача 
2. Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m2, точка которого (с массой m1 в ней) может совершать движения по горизонтальной прямой.
Решение. Вводя координату x точки m1 и угол φ между нитью маятника и вертикалью, получим:
Задача 3. Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.
Решение. В декартовых координатах x, y, z:
В цилиндрических координатах r, φ, z:
В сферических координатах r, θ, φ:
Задача 4. Выразить амплитуду xm и начальную фазу φ0 колебаний x=x(t) через начальные значения x0, v0 координаты и скорости.
Ответ: 
, 
Задача 
5. Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F.
Решение. Потенциальная энергия пружины (с точностью до малых величин высшего порядка) равна произведению силы F на удлинение δ l пружины. при x<< l имеем:
,
так что U=Fx2/2l. Поскольку кинетическая энергия есть 
то
Задача 6. Найти частоту колебаний маятника, точка подвеса которого (с массой m1 в ней) способна совершать движение в горизонтальном направлении.
|
|
|
Решение. При φ<<1 находим:
Отсюда
.
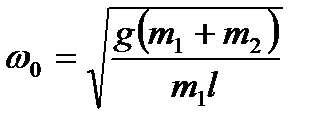Задача
7. Определить малые колебания двойного плоского маятника.
Решение. Для малых колебаний 
найденная в задаче 1 параграфа 5 функция Лагранжа принимает вид:
.
Уравнения движения:
После подстановки:
Корни характеристического уравнения:
Ответ: 
.
При 
частоты стремятся к пределам 
и 
, соответствуют независимым колебаниям двух маятников.
Задача 8. Рассмотреть следующие операторы на предмет линейности 
:
1) инверсии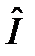 
: 
;
2) трансляции 
: 
;
3) изменения масштаба 
: 
;
4) комплексного сопряжения 
: 
.
Решение.
Представим 
в форме
, где 
и 
. (8.1)
Учтем, что соотношения 1-4 (см. условие задачи) справедливы для каждой из функций 
, входящих в суперпозицию (8.1). Тогда имеем:
1) 
;
2) 
;
3) 
;
4) 
;
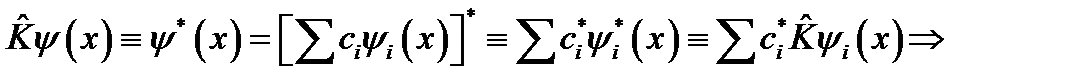
Таким образом, лишь последний из рассмотренных операторов не удовлетворяет свойству линейности.
Задача 9. Используя свойства:
1) 
, (9.1)
2) 
, (9.2)
3) 
(9.3)
скалярного произведения
, 
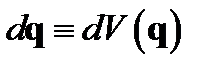. (9.4)
Доказать неравенство Коши-Шварца-Буняковского
. (9.5)
Решение.
Запишем норму функции 
вида
,
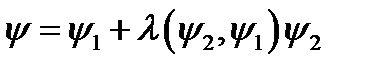где 
– вещественное число 
.
Тогда из 
с учетом (9.1)-(9.3) найдем
Ввиду произвольности 
положительность нормы 
достигается при условии неположительности дискриминанта
,
поставленного в соответствие неравенству 
. Легко видеть, что из 
, автоматически следует неравенство (9.5). Знак равенства в формуле (9.5) имеет место в том и только в том случае, когда функция 
и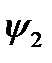 
пропорциональны друг другу, то есть
.
Задача 10. Найти оператор 
, если
1) 
, 
, 
, 
;
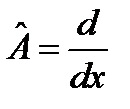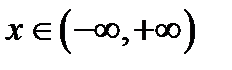2) 
, 
, 
, 
;
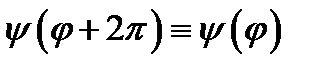Решение.
Подставляя явный вид 
в правую часть 
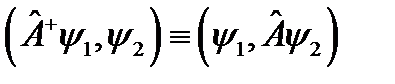и проводя интегрирование по частям, получим
1) 
,
;
2) 
,
.
Здесь использовано обращение функций 
и 
в нуль на бесконечности в случае (1) и условие периодичности функции 
и 
в случае (2). В обоих случаях оператор не совпадает с оператором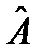 
.
|
|
|
Задача 11. Показать, что произвольный линейный оператор 
может быть представлен в виде 
, 
, 
.
Решение.
Легко видеть, что справедливо разложение на сумму
двух операторов, первый из которых является эрмитовым:
, 
,
а второй – антиэрмитовым:
.
С их помощью будем иметь:
, 
, 
,
, 
.
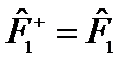Всякая линейная комбинация эрмитовых операторов с вещественными коэффициентами – эрмитов оператор. Произведение двух эрмитовых операторов не обязательно эрмитово.
Задача 12. Найти 
, если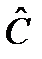 
– произведение эрмитовых операторов 
и 
.
Решение.
Из определения 
имеем
,
, 
.
Отсюда с учетом эрмитовости и найдем
. (12.1)
Легко видеть, что в общем случае 
.
Задача 13. Показать, что при условии эрмитовости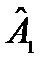 
и 
операторы 
и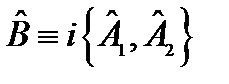 
, также эрмитовы.
Решение.
Из решения задач 11 и 12 следует, что линейному оператору 
можно поставить в соответствие два самосопряженных оператора:
, 
.
Эрмитовость операторов 
, 
и равенство (12.1) приводят к эрмитовости операторов 
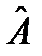и 
:
, 
.
Задача 14. Используя определение
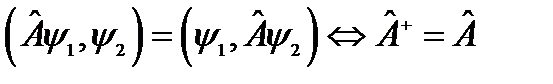(14.1)
и свойство
, (14.2)
показать, что уравнение
(14.3)
имеет решение лишь для вещественного числа 
.
Решение.
Подставляя
,
где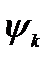 
– решение уравнения (14.3), в определение эрмитова оператора (14.1), запишем
.
Используя свойство (14.2), вынесем число 
, стоящее слева и справа от запятой, за знак скалярного произведения. Это дает
.
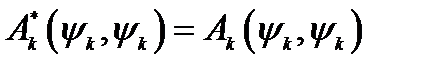Сокращая на положительное число 
, получим
.
Задача 15. Доказать, что собственные функции эрмитова оператора 
с невырожденным дискретным спектром ортогональны.
Решение.
В качестве функци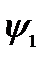и 
и 
в определении 
рассмотрим 
и 
, являющиеся решениями уравнений
, 
, (15.1)
соответственно. Воспользуемся определением (14.1) эрмитова оператора, записав его в форме
.
Подставляя сюда правые части уравнений (15.1) и учитывая свойство (14.2), получим
.
В силу вещественности и невырожденности собственных значений 
и 
, отсюда найдем
, 
, 
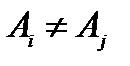, (15.2)
что и требовалось доказать.
Учтём
. (15.3)
Объединяя равенства (15.3) и (15.2), запишем условие ортонормированности
(15.4)
собственных функций эрмитова оператора с невырожденным дискретным спектром.
Задача 16. Используя свойство ортонормированности (15.2), найти коэффициенты 
разложения произвольной функции 
по базису в гильбертовом пространстве.
|
|
|
Решение.
В качестве базиса выберем собственные функции оператора 
, полученные решением уравнения (14.3) и удовлетворяющие условию (15.4). Искомое разложение представим в форме
,
где суммирование проводится по всем значениям индекса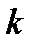 
(то есть по всем собственным значениям 
оператора 
). Для нахождения коэффициентов 
запишем скалярное произведение
.
Преобразуем его с учетом свойств (14.2), 
, (15.4). Это дает
.
Таким образом, окончательно запишем
, 
.
Коэффициент 
имеет смысл проекции функции 
на орт 
гильбертова пространства.
Задача 17. Решить уравнение (14.3) для оператора
, 
.
Решение.
Из решения задачи 10 и равенств
(17.1)
найдем
,
то есть рассматриваемый оператор 
эрмитов, а его собственные значения вещественны. Уравнение (14.3) примет вид
.
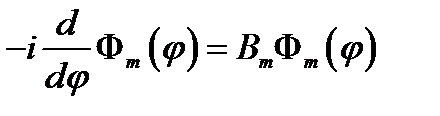Решая его, найдем
.
Из условия периодичности (см. задачу 10):
вытекает равенство
,
из которого получаем ограничение
, 
.
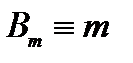Из дискретности и невырожденности спектра следует, что после нормировки (15.3) функции 
будут обладать свойством (15.4).
Запишем условие нормировки (15.3) в виде
.
В общем случае постоянный множитель есть комплексное число, однако ввиду всегда допустимого введения произвольного фазового множителя
, 
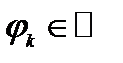(170.2)
будем предполагать вещественность константы 
. Это дает
.
Окончательно запишем
, 
.
Задача 18. Решить уравнение (14.3) для оператора
, 
.
Решение.
Из (17.1) и решения задачи 10 следует, что рассматриваемый оператор эрмитов. Следовательно, его собственные значения вещественны. Уравнение (14.3) примет вид
, 
.
Решая его, найдем
. (18.1)
Норма функции 
неограниченна, поскольку
.
Следовательно, при соответствующем выборе константы 
функции 
и 
вида (18.1) будут удовлетворять условию
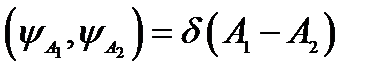. (18.2)
Для расчета 
воспользуемся равенством 
. Собственный дифференциал 
для функции (18.1) имеет вид:
,
.
Подставляя 
в определение нормы
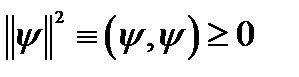, (18.3)
приходим к интегралу
,
который после замены переменных, 
, приводится к виду
.
Используя табличный интеграл
,
из условия нормировки получим
.
Как и в задаче 10, константу нормировки 
выберем вещественной. Таким образом, окончательно запишем
|
|
|
, 
. (18.4)
Задача 19. Для стационарного состояния вида
(19.1)
описывающего в одномерном случае частицу в бесконечно глубокой потенциальной яме ширины 
, рассчитать средние значения величин, соответствующих операторам:
1) 
;
2) 
.
Решение.
1) По определению
, 
, (19.2)
запишем
. (19.3)
Расчёт числителя (19.3) даёт
,
где использованы соотношения
, 
.
Аналогичным образом для знаменателя (19.3) получим
.
Следовательно, для 
будем иметь
.
2) Учитывая свойство (14.2) и определение (19.2), запишем
, 
. (19.4)
Расчёт числителя (19.4) даёт
,
.
Таким образом, для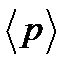 
будем иметь
.
Задача 20. В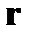 
-представлении получить явный вид оператора 
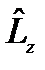, используя координаты
1) декартовы;
2) сферические.
Решение.
1) В декартовых координатах имеем
. (20.1)
2) Переход от декартовых координат 
к сферическим 
определяется формулами:
(20.2)
(20.3)
Для операторов 
и 
переход (20.2) к сферическим координатам даёт
, 
.
Подставляя эти выражения в (20.1), запишем
. (20.4)
С учетом (20.3) производные сферических координат и выражения в круглых скобках (20.4) приводятся к виду
, 
, 
, 
, 
, 
,
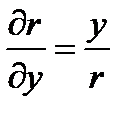(20.5)
, 
, 
, 
.
Подставляя вторую строку (20.5) в (20.4), для оператора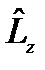 
в сферических координатах получаем
. (20.6)
Задача 21. Математический маятник совершает гармонические колебания по закону 
, 
. Найти вероятность того, что при случайном измерении отклонения 
маятника это значение будет лежать в интервале 
.
Решение.
Запишем закон колебания в виде: 
, где 
. Тогда нам надо найти вероятность: 
.
Из рисунка видно, что 
.
, 
, 
.
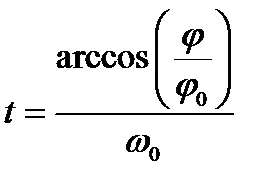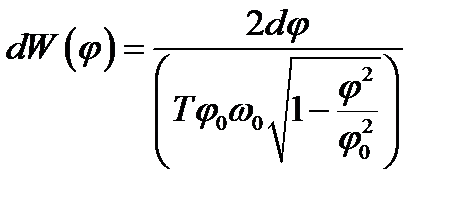Обозначим 
, 
, тогда 
.
Как и ожидалось, площадь под кривой равна 1.
Ответ.
, где .
Дополнение.
В общем случае график зависимости может не выражаться через линейные функции. Например:
Тогда необходимо подсчитать время, в течении которого параметр находится в заданном интервале значений:
.
Гамма-функция Эйлера
, 
Свойства:
, 
, 
.
Задача 22. Вероятность того, что 
и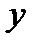 
лежат в интервалах: 
и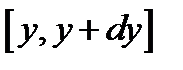 
дается выражением: 
, 
. Считая, что областями измерения переменных 
и 
являются 
и , найти константу нормировки 
.
Задача 23. Определить вероятность того, что значение величины 
будет лежать в интервале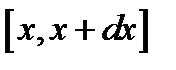 
. , .
Решение.
Условие нормировки:
, 
.
Переходим к полярным координатам:
Первому рисунку отвечает функция распределения 
, второму – 
, третьему – 
.
, 
,
, 
.
,
аналогично:
.
Ответ.
, , .
|
|
|
