Номинальные значения влияющих величин

При нормальных условиях

 

Влияющая величина	Значение
1. Температура для всех видов измерений (К)	20 (293)
2. Давление окружающего воздуха для измерения ионизирующих излучений, теплофизических, температурных, магнитных, электрических измерений, измерения давления и параметров движения, кПа (мм рт.ст.)	100 (750)
3. Давление окружающего воздуха для линейных, угловых измерений, измерения массы, силы света и измерений в других областях, кроме указанных в п.2, кПа (мм рт.ст.)	101,3 (760)
4. Относительная влажность воздуха для линейных, угловых измерений, измерений массы, измерений в спектроскопии, %
5. Относительная влажность воздуха для измерения электрического сопротивления, %
6. Относительная влажность воздуха для измерений температуры, силы, твердости, переменного электрического тока, ионизирующих излучений, параметров движения, %
7. Относительная влажность воздуха для всех видов измерений, кроме указанных в п.4-6, %
8. Плотность воздуха, кг/м	1,2
9. Ускорение свободного падения, м/с	9,8
10. Магнитная индукция (Тл) и напряженность электростатического поля (В/м) для измерений параметров движения, магнитных и электрических величин
11. Магнитная индукция и напряженность электростатического поля для всех видов измерений, кроме указанных в п. 10	Соответствует характеристикам поля Земли в данном географическом районе
12. Частота питающей сети переменного тока, Гц	50 1%
13. Среднеквадратическое значение напряжения питающей сети переменного тока, В	220 10%

 

Погрешность, обусловленная взаимодействием средства измерений иобъекта измерений. Подключение средства измерений к объекту измерений во многих случаях приводит к изменению значения измеряемой величины относительно того значения, которое она имела до подключения средства измерения к объекту измерений и определение которого является целью измерений. Эта составляющая зависит от свойств средства измерений и объекта измерений.

Классификация погрешностей средств измерений приведена на Рис. 5.

Погрешности средств измерения

Абсолютные

Приведенные

Относительные

Систематические

Случайные

Аддитивные

Мультипликативные

Статические

Динамические

Основные

Дополнительные

Рис. 5. Классификация погрешностей средств измерений

Классы точности средств измерений и нормирование

Погрешностей

На практике принято деление СИ на классы точности, которые дают их обобщенную метрологическую характеристику. Действующие стандарты (ГОСТ 8.401-80) устанавливают пределы допустимых погрешностей всех средств измерений. На показания средств измерений влияет целый ряд причин, среди которых немаловажное значение имеют внешние факторы (влияющие величины). Весь диапазон возможных значений каждой влияющей величины делится на три поддиапазона: 1) диапазон нормальных значений(область значений); 2) рабочая область значений; 3) предельная область значений.

При нормальном значении влияющей величины погрешность средств измерений минимальная.

Если влияющая величина находится в пределах рабочей области, то погрешность СИ возрастает. Если влияющая величина выходит за пределы рабочей области, то погрешность средства измерения может быть сколько угодно большой и не нормируется. Эксплуатировать средства измерения в этом случае нельзя.

Предельная область значений определяет значения влияющих величин, при которых возможно транспортирование и хранение средств измерений без изменений их метрологических свойств после возвращения в рабочие условия.

Если все влияющие величины имеют нормальные значения или находятся в пределах нормальной области значений, то условия применения средства измерений называют нормальными, а если значения влияющих величин находятся в пределах рабочих областей, то условия применения называются рабочими.

Погрешность средств измерений, используемых в нормальных условиях применения, называется основной погрешностью. Изменение погрешности средств измерений, вызванное отклонением одной из влияющих величин от нормального значения, называется дополнительной погрешностью.

В зависимости от основной и дополнительной погрешности средствам измерений на предприятии-изготовителе присваиваются соответствующие классы точности.

Класс точности средства измерений – обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых устанавливают в стандартах на отдельные виды средств измерений.

Класс точности характеризует свойства приборов в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность измерений зависит еще от метода измерений и условий, при которых выполняется измерение.

Пределы допускаемых основной и дополнительной погрешности следует выражать по форме приведенных, относительных и абсолютных погрешностей в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений конкретного вида. Пределы допускаемой дополнительной погрешности иногда можно выражать в форме, отличной от формы выражения пределов основной погрешности.

Абсолютная погрешность может быть выражена одним числом:

,

или двучленной формулой:

,

где – предел допускаемой абсолютной погрешности; а, b – положительные числа, не зависящие от x; x – значение измеряемой величины.

Коэффициент a определяет составляющую погрешности, остающуюся постоянной во всем диапазоне измерений. Эта составляющая – аддитивная погрешность. Составляющая погрешности, линейно зависящая от значения измеряемой величины, – мультипликативная погрешность, она определяется коэффициентом b.

1) В случае нормирования абсолютной погрешности классы точности обозначают прописными буквами латинского алфавита или римскими цифрами. При этом классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, соответствуют буквы, находящиеся ближе к началу алфавита, или меньшие цифры.

2) Относительная погрешность выражается одночленной формулой:

или двучленной формулой:

,

где 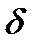– предел допускаемой относительной погрешности в процентах от значения измеряемой величины; x_к – конечное значение диапазона измерений; с,d – положительные числа. Коэффициент с численно равен относительной погрешности на верхнем пределе измерения; d численно равен погрешности на нижнем пределе измерения, выраженной в процентах верхнего предела.

Первый способ применяется для нормирования погрешности однозначных мер и масштабных преобразователей. В этом случае число, обозначающее класс точности, и предел допускаемой основной погрешности, выраженной в процентах, совпадают. Например, катушка сопротивления, для которой 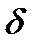= 0,01%, должны иметь условное обозначение класса точности

.

По второму способу нормируются погрешности магазинов сопротивлений ицифровых вольтметров. В обозначение класса точности входят два числа, которые разделяются чертой (первое – с, второе – d). Например, погрешность магазина сопротивлений нормируется по формуле:

,

где – показание в конце диапазона.

Условное обозначение класса точности в этом случае 0,05/4 .

Нормирование по абсолютной погрешности не позволяет сравнить приборы с разными диапазонами измерений по точности, поэтому принято нормировать приведенную погрешность:

,

где – пределы допустимой приведенной погрешности в процентах нормирующего значения Х_N.

Средствам измерений, пределы допускаемых погрешностей которых нормированы приведенной погрешностью (), присваиваются классы точности, выбираемые из ряда чисел: 1 ; 1,5 ; 2 ; 2,5 ; 4 ; 5 , где n = 1; 0; -1; -2 и т.д., (3 – не рекомендуется). Для одного и того же значения показателя разрешается устанавливать не более пяти классов точности.

Зная класс точности средств измерений, можно рассчитать пределы допускаемой относительной погрешности измерений для любого показания прибора по формуле:

,

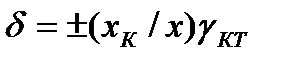где – класс точности измерительного прибора, нормированный по приведенной погрешности.

Это выражение показывает, что относительная погрешность прибора с нулем в начале шкалы, для которого (значение в конце диапазона) соответствует классу точности только при . Если намного меньше , погрешность измерения может оказаться весьма большой. Поэтому при выборе прибора необходимо учитывать не только его класс точности, но и соотношение и . Как правило, прибор должен выбираться с расчетом, чтобы измеряемая величина превышала половину диапазона измерения прибора, а относительная погрешностьне превышала приведенную погрешность более, чем в 3 раза.

Условное обозначение класса точности при его нормировании по приведенной погрешности зависит от способа выбора нормирующего значения. Если нормирующее значение определяется в единицах измеряемой величины, то класс точности обозначается числом, совпадающим с приведенной погрешностью.

Пример 1. При значении = 1,5 % класс точности обозначается 1,5 (без кружка). Таким же будет обозначение класса точности, если нормирующее значение Х _N определяется длиной шкалы (например, для омметров).

Пример 2. Катушка сопротивления, для которой относительная погрешность 0,01 %, имеет условное обозначение класса точности:

.

Погрешности многих средств электрических измерений, например, потенциометров постоянного тока, нормируются по двучленной формуле вида:

,

где e и f – постоянные числа (e = c – d; f = d ).

В последнем случае в условное обозначение класса точности входит только число e, которое заключают в кружок, т.е. обозначение класса точности не отличается от способа обозначения точности СИ с постоянной относительной погрешностью.

Пример 3. Потенциометр постоянного тока в диапазоне 0 – 50 мВ имеет основную погрешность:

,

где – показания потенциометра, мВ. Условное обозначение класса точности .

Предел допускаемой погрешности в конце диапазона измерений ( = 50 мВ) для этого потенциометра:

,

а в середине диапазона:

,

т.е. фактическая относительная погрешность прибора существенно превышает число, входящее в условное обозначение класса точности.

Пределы допускаемых абсолютных погрешностей средств измерений и возможные зависимости абсолютных погрешностей от величины показаний x показаны на Рис. 6. Пределы допускаемых относительных погрешностей средств измерений 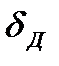и возможные зависимости относительных погрешностей от величины показаний x представлены на Рис. 7.

Рис. 6. Пределы допускаемых абсолютных погрешностей средств измерений в зависимости от величины х, где:

а) Δ_д = + а;

б) Δ_д = + (а + b x)

Рис. 7. Пределы допускаемых относительных погрешностей средств

измерений в зависимости от величины х:

Предел допускаемой приведенной погрешности γ относится к нормирующему значению Χ_N, часто принимаемому равным диапазону измерений. Приведенная погрешность γ – удобная обобщающая характеристика класса точности. Её величина определяется лишь качеством изготовления измерительного механизма и отсчетного устройства прибора и не зависит ни от значения измеряемой величины, ни от диапазона измерений.

Приведенная погрешность удобна для нормирования погрешности аналоговых электроизмерительных приборов, имеющих неизменный во всем диапазоне измерений предел допускаемой абсолютной погрешности. Нормировать погрешности аналоговых приборов в абсолютной форме нецелесообразно, поскольку однотипные приборы, но с разными диапазонами измерений (например, за счет масштабных преобразователей), будут иметь различные классы точности. Кроме того, универсальные (многодиапазонные) приборы будут иметь много различных классов точности (на каждом поддиапазоне свой класс точности). Нормировать погрешность аналоговых приборов в относительной форме тоже неудобно, поскольку относительная погрешность различна на разных отметках шкалы и, кроме того, стремится к бесконечности при уменьшении измеряемой величины до нуля.

Абсолютная и относительная погрешности результата измерений связаны с приведенной погрешностью (γ) следующими соотношениями:

 

,

где – нормирующее значение; – приведенная погрешность в соответствии с классом точности. Относительная погрешность всегда (кроме случаев ) больше приведенной. Причем, чем меньше измеренное значение x, тем больше относительная погрешность. Поэтому рекомендуется по возможности выбирать приборы таким образом, чтобы при измерениях указатель находился во второй половине шкалы. Обозначения классов точности СИ представлены в Таблице 7.

Таблица 7

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: