Определяются точечные оценки закона распределения результатов измерений.

а) Определяется точечная оценка математического ожидания (МО) – среднего арифметического измеряемой величины:

б) Определяется точечная оценка среднеквадратичного отклонения (СКО):

,

где D (x) – точечная оценка дисперсии, которая определяется по формуле:

, где n <20.

При n> 20 деление производят на n.

2. Определяют закон распределения результатов измерений либо случайных погрешностей измерений.

Для расчета погрешностей от выборки результатов измерений , ,…, переходят к выборке отклонений от среднего арифметического: , , …, , где .

По исправленным результатам измерений строят упорядоченную выборку (так называемый вариационный ряд , где , а . В вариационном ряду результаты измерений либо отклонения результатов измерений от среднего арифметического располагают в порядке возрастания.

Полученный ряд разбивают на оптимальное число «m» (как правило, одинаковых) интервалов длиной «l», так называемых интервалов группирования.

.

Оптимальным считают такое число «m», при котором возможное максимальное сглаживание случайных флуктуаций сопровождается минимальным искажением от сглаживания самой кривой распределения. Для практического применения «m» можно определять по формулам:

и .

Значение должно быть нечетным (либо середина кривой распределения искусственно уплощается). Полученное значение длины интервала «l», округляется в большую сторону,чтобы последняя точка не оказалась за пределами крайнего интервала.

Определяют интервалы группирования экспериментальных результатов в виде:

; ; … .

Затем подсчитывают число попаданий n (частоты) результатов измерений в каждый интервал группирования. Сумма частот равняется общему числу измерений . По значениям рассчитывают частости (), т.е. вероятности попадания результатов измерений в каждый из интервалов группирования:

, где k = 1, 2, …, m.

Затем на основании расчетов строят гистограмму. Для построения гистограммы по оси результатов наблюдений x откладывают интервалы 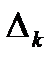(в порядке возрастания номеров) и на каждом интервале строится прямоугольник высотой . Площадь, заключенная под графиком, пропорциональна числу наблюдений n. Если высоту прямоугольника откладывать равной (эмпирической плотности вероятности), то площадь под гистограммой равна 1. С увеличением числа интервалов гистограмма приближается к гладкой кривой – графику плотности распределения вероятности (Рис. 8).

Рис.8. Гистограмма распределения вероятностей:

а) ступенчатый характер гистограммы;

б) кривая плотности распределения вероятности

Если соединить середины верхних оснований каждого столбца гистограммы, то получится ломаная кривая – полигон (Рис. 9). Полигон достаточно наглядно отражает форму кривой плотности распределения вероятности. За пределами гистограммы (справа и слева) остаются пустые интервалы, в которых точки, соответствующие их серединам, лежат на оси абсцисс. При построении полигона эти точки также учитываются, так что полигон и оси «x» образуют замкнутую фигуру, площадь которой (при использовании частостей) равна числу наблюдений.

Рис.9. Гистограмма, полигон

3. Оценка закона распределения по статистическим критериям

При числе наблюдений n> 50 чаще всего для идентификации закона распределения используют критерий согласия Пирсона χ² («хи – квадрат»).

При15 <n< 50 для проверки нормальности закона распределения применяют составной критерий («d – критерий») по ГОСТ 8.207-76.

При n< 15 соответствие экспериментального распределения нормальному распределению не проверяется.