Определение доверительных границ случайной погрешности

Для идентифицированного закона распределения находят так называемый квантильный множитель 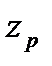при данном значении доверительной вероятности Р. Доверительный интервал случайной погрешности соответствует .

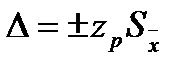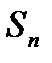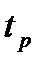При определении среднеквадратичной погрешности из малого числа наблюдений погрешность находят с малой точностью. Полученное значение не может быть заменено на . Такому доверительному интервалу соответствует меньшая вероятность. Для учета этого обстоятельства вводится так называемый коэффициент Стьюдента и равенство 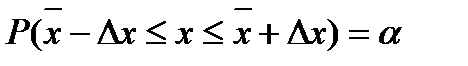заменяется равенством .

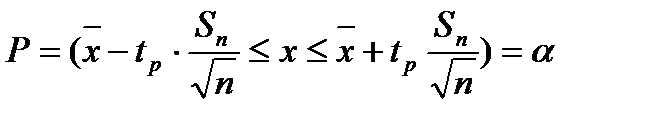Значение коэффициента Стьюдента при данном значении доверительной вероятности Р и данном числе наблюдений находится по таблицам, в частности, см. Таблицу 11.

Пример. Произведено четырехкратное измерение сопротивления катушки (результаты сведены в Таблицу 12). Определить доверительную границу погрешности результата измерений при доверительной вероятности P=0,99.

Таблица 11

Значения коэффициента Стьюдентапри доверительной вероятности

Р_д = 0,95 и Р_д = 0,99

Число наблюде­ний	Значение коэффициента tР при доверительной вероятности Р, равной	Число наблюдений	Значение коэффициента tР при доверительной вероятности Р, равной
0,95	0,99	0,95	0,99
	12,71	63,7		2,18	3,06
	4,30	9,92		2,16	3,01
	3,18	5,84		2,14	2,98
	2,77	4,60		2,13	2,95
	2,57	4,03		2,12	2,92
	2,45	3,71		2,11	2,90
	2,36	3,50		2,10	2,88
	2,31	3,36		2,09	2,86
	2,26	3,25		2,06	2,80
	2,23	3,17		2,04	2,75
	2,20	3,11		1,96	2,58

 

1. Определим среднее арифметическое из результатов четырех наблюдений:

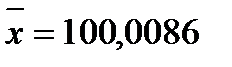Ом.

2. Найдем случайные отклонения результатов наблюдений Δ_ί. Для самопроверки определим сумму случайных отклонений. Она всегда должна равняться нулю.

3. Возьмем случайные отклонения в квадрат и найдем их сумму:

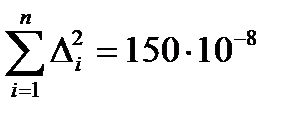Ом

Таблица 12

Четырехкратное измерение сопротивления катушки

Результат наблюдения xi , Ом	Отклонение результата наблюдения, Δί, Ом	Квадрат отклонения, Δί2, Ом2
100,0078	-0,0008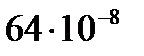
100,0084	-0,0002
100,0087	+0,0001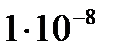
100,0095	+0,0009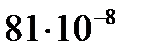

 

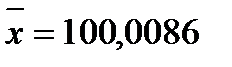
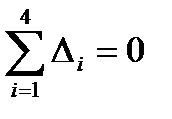
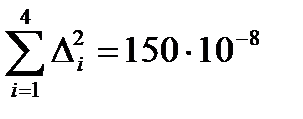
4. Найдем оценку СКО результатов наблюдений :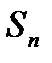

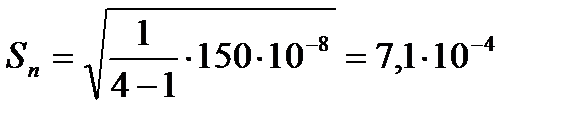Ом.

5. Найдем оценку СКО результата измерения (СКО среднеарифметического):

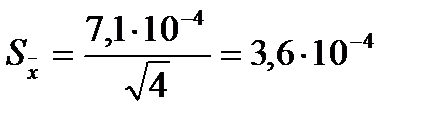Ом.

6. По Таблице 3.2 для n =4 и Р =0,99 найдем коэффициент Стъюдента t_Р =5,84.

7. Определим доверительные границы погрешности результата измерения путем умножения t_Р на :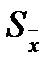

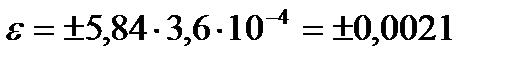Ом.

Результат измерения запишем в следующем виде:

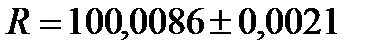Ом при Р_д =0,99.

 

 

5. Определяют границы неисключенной систематической погрешности 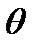результата измерений.

Эти границы находят нестатистическими методами. Это границы интервала, внутри которого находится неисключенная систематическая погрешность. Такая погрешность образуется из нескольких составляющих: погрешностей метода измерений, средств измерений, субъективной погрешности оператора. Если погрешности метода измерений и погрешности оператора малы, то границы неисключенной систематической погрешности принимаются равными пределам основных и дополнительных погрешностей средств измерения СИ (в случае, если случайные составляющие пренебрежимо малы). При определении границ 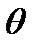доверительную вероятность принимают раной доверительной вероятности 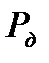, принятой при определении границ случайной погрешности.

6. Определяют доверительный интервал погрешности результата измерения ().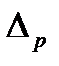

определяют суммированием СКО случайной составляющей погрешности 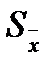и границ неисключенной систематической составляющей погрешности 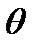в зависимости от соотношения / .

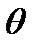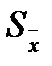7. Записывают результаты измерения.

Результаты измерения записывают в виде 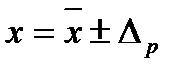при доверительной вероятности .

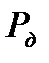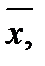
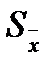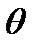Если данные о законах распределения составляющих погрешности отсутствуют, результаты приводят в следующем виде: , n, при .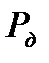

Критерии исключения грубых погрешностей

Критерий «трех сигм»

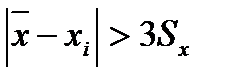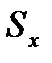Для результатов измерений (наблюдений), распределенных по нормальному закону (закону Гаусса) считается, что результат, возникающий с вероятностью Р< 0,003 (такназываемый уровень значимости q 0,3%) маловероятен, и его следует считать промахом. Таким образом, если , считается промахом. – оценка среднеквадратичного отклонения (СКО) результата наблюдения; – среднеарифметическое значение. Величины и 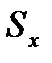вычисляются без учета экстремальных значений . Данный критерий используется предпочтительно при числе наблюдений n 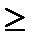20…50.

Пример 1(а). Сопротивление катушки измеряют 31 раз. =100,0086 Ом. СКО результата наблюдения 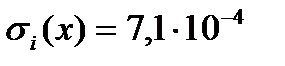Ом. Найти СКО результата измерения 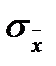и определить доверительные границы случайной погрешности результата измерений при Р 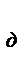= 0,95.

Решение. СКО результата измерения (СКО среднеарифметического) составит:

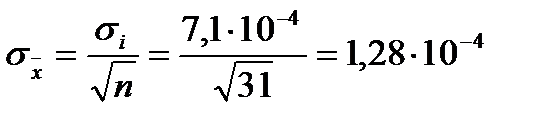(Ом).

Доверительные границы погрешности результата измерения (СКО среднеарифметического) составляют при Р 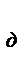= 0,95:

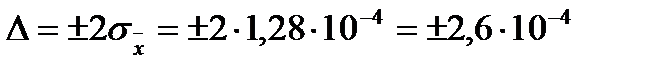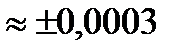(Ом) (Ом).

Таким образом, Ом (Р 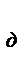= 0,95).

Пример 1(б). Сопротивление катушки измеряют 31 раз. По результатам 30 наблюдений 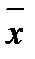= 100,0086 Ом. СКО результата наблюдения (рассчитано из 30 наблюдений) 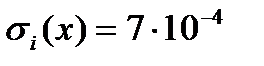Ом. Является ли 31-ый результат 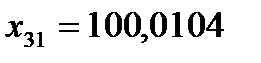Ом промахом?

Решение. По критерию «трех сигм» промахом будет считаться результат, для которого 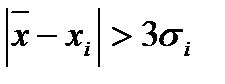, т.е. 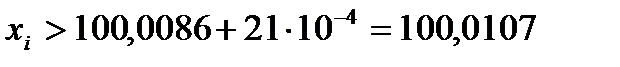Ом и 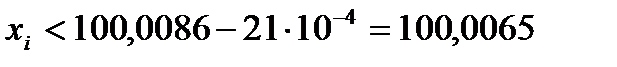Ом. Результат 31-го наблюдения 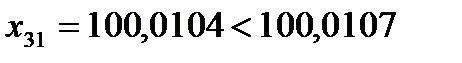Ом, т.е. результат данного наблюдения меньше максимально допустимого, но больше минимально допустимого, промахом не является и его следует включить в статистическую обработку.

Критерий Романовского.

Если число измерений менее 20 (n <20), одним из рекомендованных критериев исключения грубых погрешностей является критерий Романовского. Для проверяемого значения вычисляют отношение

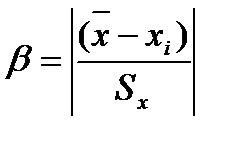
и сравнивают с табличным значением критерия Романовского 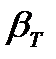. Значения критерия 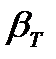, в зависимости от числа наблюдений n и уровня значимости q (так называемой вероятности невыполнения), вычисляют по таблицам.

 

Таблица 13

Значения критерия Романовского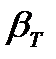

q	n= 4	n =6	n =8	n =10	n =12	n =15	n =20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,03	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,1	1,69	2,00	2,17	2,29	2,39	2,49	2,62

Если 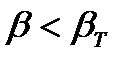, результат считают правильным. Если 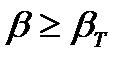, результат считают промахом и отбрасывают.

Пример. Результаты 5 измерений расхода топлива автомобиля составили 12, 14, 16, 18 и 20 л на 100 км. Проверить, не является ли последний результат промахом.

Среднеарифметическое значение и его СКО (без учета последнего наблюдения, расчет по 4-м результатам): =15 л; СКО =2,6 л. Из Таблицы 1.13 следует, что при уровне значимости 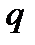=0,01 и n =4 коэффициент 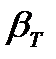=1,73. Для последнего наблюдения 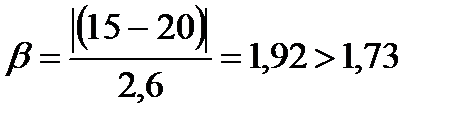, т.е. полученное значение β больше табличного. Согласно критерию Романовского, результат последнего наблюдения необходимо отбросить.

Существуют и другие критерии, например, вариационный критерий Диксона, критерий Шарлье, критерии Граббса и Шовенэ. Применение статистических критериев требует осмотрительности. Отличающиеся от других результаты наблюдений не следует сразу отбрасывать. Лучше провести дополнительные измерения (не вместо сомнительных, а в дополнение к ним), а затем привлекать статистические критерии.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: