Колебания в однородных цепочках

Анализ колебаний в системе с n степенями свободы значительно упрощается, если система представляет собой цепочку последовательно включенных однородных элементов. Рассмотрение собственных колебаний в такой цепочке представляет интерес в связи с тем, что цепочка является одномерным аналогом кристаллической решётки, состоящей из одинаковых атомов.

Рис. 75. Схема однородной цепочки.

Рассмотрим колебания в однородной цепочке на примере полосового фильтра, изображённого на рис. 75. Выберем в качестве независимых координат заряды q_l, прошедшие к моменту времени t через поперечное сечение соответствующих катушек. Выражения для кинетической и потенциальной энергии такого фильтра имеют вид:

,  ,

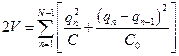тогда уравнение Лагранжа (1.30) может быть записано так:

.

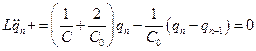(8.32)

Уравнение (8.32) справедливо для любого звена цепочки, кроме первого и последнего. Заряды в первом и (N + 1)-м звеньях цепочки определяются граничными условиями. Рассмотрим случай системы с разомкнутыми концами, т. е. q ₁ = 0, q_{N + 1} = 0.

Будем искать решение системы ДУ (8.32) в виде

.

Подстановка в уравнение (8.32) даёт разностные уравнения:

,  n = 2,…, N.

(8.33)

Здесь n ² = 1/ LC + 2/ LC ₀ - квадрат парциальной частоты одного звена, a = 1/ LC ₀ - коэффициент связи. Решение системы разностных уравнений (8.33) можно записать следующим образом:

.

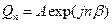После подстановки решения в (8.33) получим

,

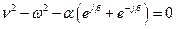или

.

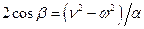(8.34)

Величина b представляет собой сдвиг фаз на одном элементе цепочки. Поэтому уравнение (8.34) связывающее частоту колебаний w и сдвиг фаз b, называется дисперсионным уравнением цепочки.

Действительным фазовым сдвигам в уравнении (8.34) отвечает условие:

.

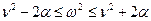(8.35)

Каждому значению частоты w из интервала (8.35) соответствуют два одинако­вых по модулю и разных по знаку значения параметра b дисперсионного урав­нения (8.34). Таким образом, общее решение системы разностных уравнений (8.33) имеет вид

.

(8.36)

Для нахождения собственных частот колебаний цепочки воспользуемся граничными условиями

,  .

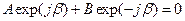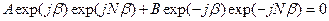Видно, что эта система совместна, если exp(2 jNb) = 1, или b = sp / N и B = - A exp(-2 jb). Используя соотношение (8.34), найдём собственные частоты

.

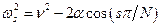(8.37)

Так как цепочка с разомкнутыми концами (q ₁ = 0, q_{N + 1} = 0) представляет собой систему с N - 1 степенями свободы, то у неё N - 1 различных собственных частот w_s, s = 1,…, N - 1, лежащих в полосе прозрачности системы (8.35). Значения s = 0 и s = N дают критические частоты

,  .

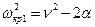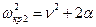Из уравнения (8.36) можно найти амплитуды Q_ns:

.

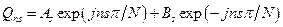(8.38)

Таким образом, собственные колебания цепочки из N + 1 одинаковых элементов с разомкнутыми концами могут быть описаны как

,  n = 1,…, N + 1.

(8.39)

Здесь параметры D_s и j_s определяются начальными условиями. Собствен­ные колебания n -го звена цепочки представляют собой суперпозицию N - 1 нормальных колебаний. Распределение амплитуд по координатам для каждой собственной частоты происходит по синусоидальному закону. При w = w ₁ колебания во всех элементах цепочки происходят в фазе, и на длине цепочки укладывается одна полуволна. С увеличением номера s количество полуволн, укладывающихся вдоль цепочки, растёт. На s -й собственной частоте (w = w_s) число полуволн равно s.

Рис. 76.Т-разбиение однородной цепочки с внешней силой и нагрузкой на конце.

При анализе вынужденных колебаний предположим, что на одном конце цепочки действует гармоническое напряжение u ₀(t) = U ₀exp(jwt), а другой конец нагружен произвольным сопротивлением Z_н. Используем Т-разбиение, т. е. представим цепочку в виде последовательно соединённых Т-образных четырёхполюсников (рис.76).

Запишем для n -го звена уравнения Кирхгофа:

, .

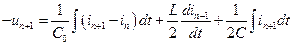(8.40)

Будем решать эту систему методом комплексных амплитуд, положив

,  .

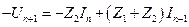(8.41)

Здесь Z ₁ - полное сопротивление последовательно соединённых индуктивности L /2 и конденсатора 2 C, а Z ₂ - полное сопротивление конденсатора C ₀.

Решение системы разностных уравнений (8.41) ищем в виде

,  ,

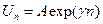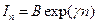где g в общем случае может быть комплексной величиной: g = d + jb. Подстановка предполагаемого решения в (8.41) даёт два линейных однородных уравнения относительно комплексных амплитуд A и B:

,  .

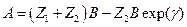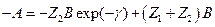(8.42)

Система уравнений (8.42) имеет нетривиальное решение, когда её детерминант равен нулю, что приводит к условию:

.

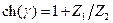(8.43)

Последнее выражение даёт связь между частотой внешней силы w и величиной g, определяющей характер процесса.

Рассмотрим отдельно две возможности: |1 + Z ₁/ Z ₂| £ 1, |1 + Z ₁/ Z ₂| > 1. Для рассматриваемой схемы неравенство |1 + Z ₁/ Z ₂| £ 1 справедливо, если частота w лежит в пределах

.

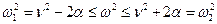(8.44)

В этом случае g - чисто мнимая величина, причём существуют два различающихся знаками значения: g ₁ = jb, g ₂ = - jb. Общее решение системы (8.41) при этом имеет вид:

,  .

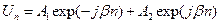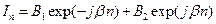(8.45)

Для каждого значения g, удовлетворяющего условию (8.43), из уравнения (8.42) можно найти отношение комплексных амплитуд A и B:

,  .

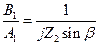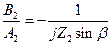Таким образом, решения (8.45) можно записать в виде

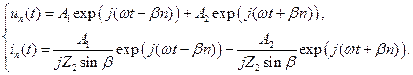
(8.46)

Каждое из слагаемых системы (8.46) можно рассматривать как бегущую волну, фаза в которой меняется не непрерывно, а скачком на b при переходе от n -го звена цепочки к n + 1-му.

Мы предположили, что входным звеном цепочки, к которому приложено внешнее напряжение, служит звено с номером n = 0. В (8.46) первые слагаемые соответствуют волне, бегущей от источника, а вторые - волне, отражённой от нагрузки. Амплитуды этих волн можно определить из граничных условий

,  .

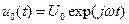Отсюда легко найти отношение A ₂/ A ₁ на конце цепочки, то есть при n = N:

.

Вводя обозначение Z ₀ = jZ ₂sin b - волновое сопротивление цепочки, перепишем в виде

.

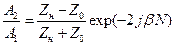(8.47)

Если сопротивление нагрузки Z_н равно Z ₀, то, как видно из последнего соотношения, отражённая волна в цепочке отсутствует. Для рассматриваемой цепочки (рис. 76)

.

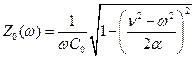(8.48)

Если Z_н ¹ Z ₀, то наряду с волной, бегущей от источника, существует и отраженная волна. Решение (8.46) при этом имеет вид:

(8.49)

Отношение комплексной амплитуды отраженной волны к комплексной ампли­туде падающей волны называется коэффициентом отражения в n -м звене:

.

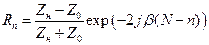(8.50)

При Z_н ¹ Z ₀ лишь часть энергии поглощается в нагрузке, а остальная часть воз­вращается к источнику энергии.

Для короткозамкнутой цепочки (Z_н = 0) и разорванной цепочки (Z_н ® ¥) из уравнения (8.50) следует, что | R_n | = 1, и в цепочке существует чисто стоячая волна. Так, для Z_н = 0

, где  ;

для Z_н ® ¥

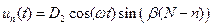, где  .

Для чисто стоячей волны поток энергии от источника к нагрузке равен нулю. Амплитуда A ₁ здесь определяется из граничного условия u ₀(t) = U ₀exp(jwt).

Кроме волнового сопротивления практически важны следующие параметры цепочки:

а) входное сопротивление, определяемое как отношение напряжения к току на входе линии:

;

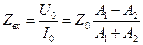б) коэффициент передачи цепочки, т. е. отношение напряжения выходного сигнала к напряжению входного:

.

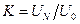В согласованном режиме при Z_н = Z ₀ коэффициент передачи | K | = 1.

Рассмотрим теперь второй возможный случай: |1 + Z ₁/ Z ₂| > 1. Это неравенство справедливо либо при b = 0 и ch d > 1, либо при b = p и ch(d + ip) = -ch d < -1. В этом случае выделяются две области частот. Область частот, для которых b = 0 и ch d > 1, располагается между нулём и частотой w ₁, т. е.

.

В этом диапазоне значений w решение (8.41) принимает вид:

.

Первое слагаемое здесь характеризует колебатель­ный процесс, при котором все звенья колеблются в фазе, но амплитуда колеба­ний экспоненциально уменьшается вдоль цепочки в направлении увеличения номера, а второе - отраженную вол­ну. При большом числе звеньев (dN >> 1) процесс затухнет раньше, чем колебания достигнут нагрузки. При выполнении этого условия отражённую волну (второе слагаемое) можно не учитывать. В этом случае коэффициент передачи для цепочки

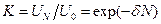
(8.51)

падает с ростом числа звеньев N, т. е. достаточно длинная цепочка не пропускает колебания с частотой w < w ₁.

Область частот, для которых b = p и |ch d | > 1, простирается от w ₂ до бесконечности:

.

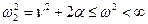Решение для этой области частот имеет вид:

.

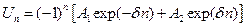Рис. 77. Коэффициент передачи полосового фильтра.

По-прежнему, при большом числе звеньев dN >> 1 отражённую волну можно не учитывать. Однако, в области частот w > w 2 соседние звенья цепочки колеблются в противофазе. Коэффициент передачи и в этом случае описывается формулой (8.51) и при dN >> 1 очень мал. Таким образом, рассмотренная цепочка представляет собой полосовой фильтр (рис. 77), пропускающий частоты, лежащие в полосе

прозрачности (8.44), и отфильтровывающий частоты w < w ₁ и w > w ₂. Частоты w ₁ и w ₂ являются граничными частотами фильтра.

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: