Вынужденные колебания в распределённых системах

По аналогии с вынужденными колебаниями в системах с многими степе­нями свободы удобно раскладывать и вынуждающую силу, и вынужденные колебания по собственным функциям системы. Если частота внешней силы совпадает с одной из собственных частот системы, то происходит резонансное увеличение амплитуды колебаний.

Рассмотрим разомкнутую на концах двух­проводную линию с потерями, в которой действует распределённая внешняя сила. Подставляя в первое уравнение системы (9.9) 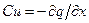, , 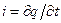получим

,

(9.16)

где L, C, R - постоянные погонные параметры линии.

Пусть линия разомкнута на обоих концах, т. е. q (0, t) = q (l, t) = 0. Разложим внешнюю силу в ряд на интервале 0 £ x £ l по собственным функциям вида (9.14) разомкнутой на концах линии

,

(9.17)

а коэффициенты разложения найдём, используя условие (9.15) ортогональности собственных функций:

.

(9.18)

Естественно искать решение уравнения (9.16) также в виде ряда по собственным функциям линии с разомкнутыми концами

.

(9.19)

Подставим (9.17) и (9.19) в исходное уравнение (9.16):

,  n = 1, 2, …

(9.20)

Получилась бесконечная система обыкновенных ДУ относительно Q_n (t). Каждое из них имеет обычный вид колебательного уравнения для системы с одной степенью свободы, на которую действует внешняя сила U_n (t). Уравнения независимы, и поэтому Q_n (t) можно рассматривать как нормальные координаты системы. Число таких координат бесконечно. Если отсутствует какая-либо компонента внешней силы U_n (t), то соответствующая координата Q_n (t) совершает только свободное затухающее колебание.

Решение уравнений (9.20) может быть записано через интеграл Дюамеля:

.

(9.21)

Здесь обозначено: , , .

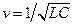Для гармонического синхронного и синфазного внешнего воздействия U_n (t) = U_{n 0}exp(jw ₀ t) в установившемся режиме при t >> 1/ d получаем

.

Суммируя по всем n, получим общее решение уравнения (9.20) в виде

.

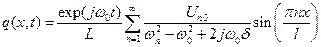(9.22)

Если частота внешнего воздействия w ₀ совпадает с одной из собственных частот системы w_n, то наблюдается резонансное увеличение амплитуды.

В ча­стном случае, если гармоническое внешнее воздействие приложено в одной точке x = b, получаем:

,

где d (x) - дельта-функция. Определим коэффициенты разложения функции u ₀(x, t)

.

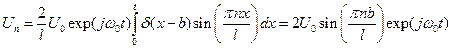Общее решение в этом случае будет иметь вид

.

(9.23)

Нетрудно видеть, что если b = l / n, т. е. внешняя сила приложена к узлу, то q (x, t). Это явление аналогично ортогональности вынуждающей силы на од­ной из собственных частот системы и собственного колебания на этой частоте для системы с многими степенями свободы.

Лазер как автогенератор

Примером автоколебательной системы с распределенными параметрами является оптический квантовый генератор - лазер. Распределенное отрицатель­ное сопротивление в лазере создается активной средой с инверсной населенно­стью и существует в определенной полосе частот вблизи линии поглощения среды. Как правило, в пределах ширины линии люминесценции укладывается несколько собственных частот резонатора, поэтому лазер, в общем случае, генерирует ряд мод с частотами, близкими к собственным частотам резонатора.

Анализ работы лазера обычно проводится методом самосогласованного поля в полуклассическом приближении. Предполагается, что электромагнитное поле, воздействуя на активную среду, создает в ней поляризацию, которая, в свою очередь, является источником электромагнитного поля. При этом элек­тромагнитное поле описывают классическими уравнениями Максвелла, а поля­ризацию среды, определяющую отрицательное нелинейное сопротивление, рас­сматривают на квантовом уровне. При таком подходе поляризация среды зависит не от мгновенного значения напряженности поля, а от его амплитуды, то есть лазер является автогенератором с инерциальной нелинейностью, анало­гичным рассмотренному в пункте 6.2.

В простейшем случае оптического резонатора Фабри-Перро, образованного двумя плоскими зеркалами, расположенными на расстоянии l друг от дру­га, наибольшую добротность имеют аксиально симметричные моды колебаний. Электромагнитное поле таких колебаний медленно меняется в пространстве в направлении, параллельном зеркалам, а его поляризация сохраняется. Это по­зволяет ограничиться рассмотрением одномерного скалярного уравнения Мак­свелла, которое для проводящей немагнитной среды принимает вид

.

(9.24)

Будем считать, что величина s характеризует все виды потерь энергии в оптическом резонаторе.

Напряжённость электрического поля можно представить в виде ряда по собственным функциям нормальных мод резонатора

,

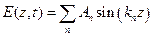(9.25)

где k_n = pn / l = 2 p / l_n - волновое число n -го нормального колебания. Такой вид нормальных колебаний соответствует граничным условиям E (0, t) = E (l, t) = 0, когда в точках z = 0 и z = l находятся зеркала с единичным коэффициентом от­ражения. Умножим уравнение (9.24) на sin(k_mz) и проинтегрируем по z от 0 до l. Учитывая ортогональность собственных функций разложения (9.25) и гранич­ные условия, получим

,

(9.26)

где Q_n - добротность резонатора на n -й моде, w_n - частота n -й моды, W _n = pnc / l - собственная частота резонатора, P_n - пространственная фурье-компонента поляризации среды, равная

.

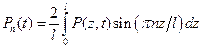При достаточно высокой добротности резонатора и небольшой величины поляризации, когда лазер работает вблизи порога самовозбуждения, для реше­ния уравнения (9.26) можно использовать метод ММА. Будем искать решение (9.26) в виде

,  ,

где E_n (t), j_n (t) - медленно меняющиеся за период 2 p / w_n амплитуда и фаза n -го колебания, C_n (t) и S_n (t) - медленно меняющиеся компоненты поляризации. В си­лу инерциальной нелинейности активной среды можно считать, что компонен­ты поляризации являются нечётными функциями амплитуд колебаний вида

,  .

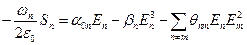(9.27)

Уравнения (9.27) являются материальными уравнениями нелинейной ак­тивной среды, в них опущены колебания комбинационных частот, не попадаю­щие в полосы пропускания оптического резонатора. Коэффициенты уравнений (9.27) для двухуровневого газового лазера рассчитаны У. Лэмбом. С учетом этих соотношений укороченные уравнения для системы (9.26) принимают вид

,	(9.28)
.	(9.29)

Из уравнения (9.28), в частности, следует, что величина a _{0 n} определяет усиление активной среды на n -й моде колебаний для слабого сигнала. Поэтому условие самовозбуждения n -й моды можно записать в виде a _{0 n} > w_n /(2 Q_n). При выполнении этого условия поступление энергии в систему превышает потери в резонаторе на соответствующей частоте.

Рассмотрим сначала случай возбуждения в системе только одной моды, единственной, для которой выполняется условие самовозбуждения. Уравнения (9.28) и (9.29) в этом случае принимают вид:

,  .

Отсюда можно найти стационарную амплитуду и частоту генерации

,  ,

где обозначено a = a ₀ - w /(2 Q). Отметим, что амплитуда установившихся коле­баний E ₀ тем больше, чем больше поступление энергии в систему превышает по­тери в ней. Кроме того, E ₀ зависит от коэффициента нелинейности b, как это имеет место и в одноконтурном автогенераторе (см. пункт 6.2). Этот коэффициент определяет уменьшение инверсной населённости, связанное с насыщением активной среды, вызванным колебаниями генерируемой моды. При малой амплитуде частота генерации w отличается от собственной частоты резонатора на величину . Коэффициент s пропорционален разности между собственной частотой резонатора и частотой спектральной линии атомного перехода. Поэтому он создаёт линейное подтягивание генерируемой частоты к частоте атомного перехода. Нелинейное сла­гаемое даёт зависящее от амплитуды смещение частоты генерации.

Если усиление активной среды превышает потери для двух собственных частот оптического резонатора, то возможна одновременная генерация двух не­зависимых мод колебаний. В случае двухмодового режима укороченные уравнения (9.28) для амплитуд E ₁ и E ₂ принимают вид:

,  .

(9.30)

Здесь a ₁ = a ₀₁ - w ₁/(2 Q ₁), a ₂ = a ₀₂ - w ₂/(2 Q ₂) - коэффициенты, характеризующие превышение усиления над потерями для каждой из мод. Коэффициенты q ₁₂ и q ₂₁ определяют уменьшение инверсной населенности для каждой моды, вызванное колебаниями другой моды, т. е. эквивалентны коэффициентам связи.

Урав­нения (9.30) удобно переписать для квадратов амплитуд , :

,  .

(9.31)

Система уравнений (9.31) имеет четыре стационарных решения:

;  , ;  , ; , .

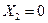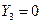(9.32)

Первое решение соответствует отсутствию генерации, второе и третье - генера­ции одной моды. Четвертое решение описывает режим одновременной генера­ции двух мод.

Устойчивость стационарных решений можно определить стан­дартным методом, анализируя малые отклонения от стационарного состояния.

Коэффициенты b ₁ и b ₂ для активной среды всегда положительны. Если оба коэффициента a ₁ и a ₂ положительны, т. е. условия самовозбуждения выпол­нены для обеих мод, то режим покоя неустойчив. При a ₁/ q ₁₂ > a ₂/ b ₁ и a ₂/ q ₂₁ < a ₁/ b ₂ система генерирует одну моду с X = a ₁/ b ₁, Y = 0. Вторая мода по­давляется модой с большим коэффициентом усиления. Если же a ₁/ q ₁₂ > a ₂/ b ₁ и a ₂/ q ₂₁ > a ₁/ b ₂, то в системе могут существовать обе моды колебаний. При сла­бой связи b ₁ b ₂ > q ₁₂ q ₂₁ происходит одновременная генерация обеих мод.

Ам­плитуды и частоты этих колебаний в стационарном режиме в силу соотношений (9.29) и (9.32) имеют вид

,  .	(9.33)
,  .	(9.34)

Из формулы (9.34), в частности, следует, что частота каждого из колебаний за­висит не только от его амплитуды, но и от амплитуды второго колебания.

Список рекомендуемой литературы [1]

1. Основы теории колебаний: Учеб. руководство/Под ред. В. В. Мигулина.- М.: Наука, 1988.- 392с.

2. Капранов М. В., Кулешов В. Н., Уткин Г. М. Теория колебаний в радиотехнике: Учебное пособие для вузов.- М.: Наука, 1984.- 320с.

[1] Конечно же, основным источником литературы для составления этого учебного пособия послужили лекции В. К. Игнатьева.

⇐ Предыдущая15161718192021222324

Поделиться:

Воспользуйтесь поиском по сайту: