 |
Исследование функций с помощью производной
|
|
|
|
1. Условия постоянства, возрастания и убывания функций
Пусть f (x) определена в V (x 0).
Определение 1. Функция f называется возрастающей в точке x 0, если $ V (x 0, d) точки x 0, такая, что
f (x)< f (x 0) при x < x 0(" x Î(x 0 -d, x 0),
f (x)> f (x 0) при x>x 0(" x Î(x 0, x 0+ d).
Определение 2. Функция f называется убывающей в точке x 0, если $ V (x 0, d) точки x 0, такая, что
f (x)> f (x 0) при x < x 0(" x Î(x 0 -d, x 0),
f (x)< f (x 0) при x>x 0(" x Î(x 0, x 0+ d).
Теорема 1. Если функция f дифференцируема в точке x 0 и f¢ (x 0)>0 (f¢ (x 0)<0), то f возрастает (убывает) в точке x 0.
Доказательство.
 По определению производной
По определению производной 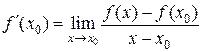 .
.
Пусть f¢ (x 0)>0 (случай f¢ (x 0)<0 доказывается аналогично). По определению предела функции по Коши получаем:
" e >0 (e = f¢ (x 0)) $ d >0: " x: | x-x 0|< d выполнено  Û
Û  Û
Û  (1)
(1)
(1) выполнено  .
.
Возьмем  , т. е. x Î(x 0 -d, x 0) Þ x-x 0<0. Тогда из того, что
, т. е. x Î(x 0 -d, x 0) Þ x-x 0<0. Тогда из того, что  Þ f (x)< f (x 0).
Þ f (x)< f (x 0).
Возьмем  , т. е. x Î(x 0, x 0+ d) Þ x-x 0>0. Тогда из того, что
, т. е. x Î(x 0, x 0+ d) Þ x-x 0>0. Тогда из того, что  Þ f (x)> f (x 0).
Þ f (x)> f (x 0).
На основании определения 1 функция f возрастает в точке x 0. 
Замечание. Условие f¢ (x 0)>0 (f¢ (x 0)<0) не является необходимым для возрастания (убывания) функции в точке x 0. Т. е. из того, что f (x) возрастает (убывает)в точке x 0 не следует, что f¢ (x 0)>0 (f¢ (x 0)<0).
 Пример. D f (x)= x 3,
Пример. D f (x)= x 3,  . Рассмотрим точку x =0.
. Рассмотрим точку x =0.
f¢ (x)=3 x 2, f¢ (0)=0, но в точке х =0 функция возрастает. D
Теорема 2 (признак постоянства функции) Пусть функция f определена и непрерывна на [ a; b ] и дифференцируема на (a; b). Для того, чтобы f (x) была постоянной на [ a; b ] необходимо и достаточно, чтобы f¢ (x)=0 " x Î(a; b).
Следствие. Пусть f (x), g (x) определены и непрерывны на [ a; b ] и дифференцируемы на (a; b). Если f¢ (x)= g¢ (x)" x Î(a; b), то f (x), g (x) отличаются друг от друга на постоянную.
Доказательство следует из теоремы 2 (применить для функции F (x)= f (x) -g (x)).
|
|
|
Теорема 3 (признак монотонности функции). Пусть функция f определена и непрерывна на [ a; b ] и дифференцируема на (a; b). Функция не убывает (не возрастает) на [ a; b ] Û f¢ (x)³0 (f¢ (x)£0) на (a; b).
Доказательство.
 1) Необходимость.
1) Необходимость.
Пусть f не убывает на (случай невозрастания доказывается аналогично).
Тогда по определению " x, x 0Î[ a; b ]: x < x 0 Þ f (x)£ (x 0) Þ  ,
,
" x, x 0Î[ a; b ]: x > x 0 Þ f (x)³ (x 0) Þ  .
.
Следовательно,  , т. е.
, т. е.  . Т. к. x 0Î[ a; b ] - произвольная точка, то необходимость доказана.
. Т. к. x 0Î[ a; b ] - произвольная точка, то необходимость доказана.
2) Достаточность.
Пусть f¢ (x)³0 на (a; b) (случай f¢ (x)£0 доказывается аналогично). Возьмем " x 1, x 2Î[ a; b ]: x 1< x 2. К [ x 1; x 2] применим теорему Лагранжа: $ с Î(x 1; x 2):
f (x 2) -f (x 1)= f¢ (c)(x 2 -x 1). Т. к. f¢ (с)³0, x 2 -x 1>0, то f (x 2) -f (x 1)³0. Т. е. f (x 2)³ f (x 1). По определению функция не убывает на [ a; b ]. 
Теорема 4. Пусть функция f определена и непрерывна на [ a; b ] и дифференцируема на (a; b). Если f¢ (x)>0 (f¢ (x)<0), то f возрастает (убывает) на (a; b).
Доказывается так же, как и п. 2) теоремы 3.
Замечание. Условие теоремы 4 является достаточным, а не необходимым. Например, функция y = x 3 возрастает на  , а f¢ (0)=0.
, а f¢ (0)=0.
2. Экстремум функции
Пусть f (x) определена в V (x 0).
Определение 1. Точка х = х 0 называется точкой максимума функции f, если существует окрестность V (x 0, d)Ì V (x 0), в пределах которой выполнено неравенство f (x)£ f (x 0).
Значение функции в точке x 0 называется максимумом функции.
Определение 2. Точка х = х 0 называется точкой минимума функции f, если существует окрестность V (x 0, d)Ì V (x 0): " x Î V (x 0, d) выполнено f (x)³ f (x 0).
Значение функции в точке x 0 называется минимумом функции.
Определение 3. Точка х = х 0 называется точкой строгого максимума (строгого минимума) функции f, если существует V (x 0, d)Ì V (x 0): " x Î V (x 0, d) выполнено неравенство f (x)< f (x 0) (f (x)> f (x 0)).
Значение функции в точке x 0 называется строгим максимумом (строгим минимумом) функции.
|
|
|
Точки максимума и минимума называются точками экстремума, а значения функции в них – экстремумами функции.
Можно доказать, что если функция непрерывна на (a; b) и имеет несколько максимумов и минимумов, то они чередуются. Понятия максимума и минимума являются локальными, т. е. понятиями, относящимися не ко всей области определения функции, а только к окрестности некоторой точки. Не следует смешивать понятия максимума и минимума с наибольшим и наименьшим значением функции на < a; b >. Функция f может иметь несколько максимумов (минимумов), но они не будут наибольшими (наименьшими) значениями функции. Функция может иметь наибольшее и наименьшее значения, но они не будут ни максимумом, ни минимумом.

 Теорема 5 (необходимое условие экстремума). Пусть f (x) определена в V (x 0). Если функция имеет в точке x 0 экстремум, то производная функции в этой точке равна нулю или не существует.
Теорема 5 (необходимое условие экстремума). Пусть f (x) определена в V (x 0). Если функция имеет в точке x 0 экстремум, то производная функции в этой точке равна нулю или не существует.
Доказательство.
 По условию функция имеет в точке x 0 экстремум. Следовательно, существует окрестность V (x 0, d)Ì V (x 0), в пределах которой f (x 0) является наибольшим или наименьшим значением функции f. По теореме Ферма, если существует f ¢(x 0), то f ¢(x 0)=0. Для завершения доказательства приведем пример, когда функция, не дифференцируемая в точке, имеет в этой точке экстремум.
По условию функция имеет в точке x 0 экстремум. Следовательно, существует окрестность V (x 0, d)Ì V (x 0), в пределах которой f (x 0) является наибольшим или наименьшим значением функции f. По теореме Ферма, если существует f ¢(x 0), то f ¢(x 0)=0. Для завершения доказательства приведем пример, когда функция, не дифференцируемая в точке, имеет в этой точке экстремум.
y =| x |, 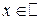 .
.
х =0 – точка минимума, т. к. f (0)=0 и " х ¹0 f (x)>0, но f (x) не дифференцируема в точке х =0. 
Определение. Пусть f (x) определена в V (x 0). Точка x 0 называется стационарной точкой функции f, если f ¢(x 0)=0. Точка x 0 называется критической точкой функции f, если f ¢(x 0)=0 или не существует.
Из теоремы 4 следует, что точками экстремума могут быть только критические точки. Обратное не всегда верно.
Пример. D f (x)= x 3, f ¢(x)=3 x 2, f ¢(0)=0.Но х =0 не является точкой экстремума. Действительно, при x <0 f (x)<0, а при x >0 f (x)>0. Следовательно, х =0 не является ни точкой максимума, ни точкой минимума. D
Т. о., критические точки являются точками возможного экстремума. Найдя критические точки, необходимо подвергнуть их дальнейшему исследованию.
Теорема 6 (первое достаточное условие экстремума). Пусть f дифференцируема в некоторой окрестности точки x 0, кроме, быть может, самой точки x 0, в которой она непрерывна. Пусть f ¢(x) сохраняет знак в отдельности как слева, так и справа от точки x 0, т. е. в интервалах (x 0 -d; x 0), (x 0; x 0 -d). Если:
|
|
|
1) f ¢(x)>0 при x<x 0 и f ¢(x)<0 при x > x 0, то x = x 0 - точка строгого максимума;
2) f ¢(x)<0 при x<x 0 и f ¢(x)>0 при x > x 0, то x = x 0 - точка строгого минимума;
3) f ¢(x)>0 или f ¢(x)<0 " x Î V (x 0), то x = x 0 не является точкой экстремума.
Доказательство.

 1) Возьмем " x Î V (x 0, d). Применим теорему Лагранжа к отрезку [ x 0; x ] или [ x; x 0]. Получим (1) f (x)- f (x 0)= f ¢(c)(x-x 0), c Î(x 0; x) (или с Î(x; x 0)). Пусть x < x 0 Þ x - x 0<0. Т. к. с<x 0, то f ¢(c)>0. Из (1) Þ f (x)- f (x 0)<0, т. е. f (x)< f (x 0). Пусть x>x 0 Þ x - x 0>0. Т. к. с>x 0, то f ¢(c)<0. Из (1) Þ f (x)- f (x 0)<0, т. е. f (x)< f (x 0). Следовательно, " x Î V (x 0, d) f (x)< f (x 0). Значит, то x = x 0 - точка строгого максимума.
1) Возьмем " x Î V (x 0, d). Применим теорему Лагранжа к отрезку [ x 0; x ] или [ x; x 0]. Получим (1) f (x)- f (x 0)= f ¢(c)(x-x 0), c Î(x 0; x) (или с Î(x; x 0)). Пусть x < x 0 Þ x - x 0<0. Т. к. с<x 0, то f ¢(c)>0. Из (1) Þ f (x)- f (x 0)<0, т. е. f (x)< f (x 0). Пусть x>x 0 Þ x - x 0>0. Т. к. с>x 0, то f ¢(c)<0. Из (1) Þ f (x)- f (x 0)<0, т. е. f (x)< f (x 0). Следовательно, " x Î V (x 0, d) f (x)< f (x 0). Значит, то x = x 0 - точка строгого максимума.
2) Аналогично.
3) Пусть f ¢(x)>0 " x Î  .
.
Если x < x 0, т. е. x - x 0<0, то из (1), т. к. f ¢(c)>0, следует f (x)- f (x 0)<0, т. е. f (x)< f (x 0).
Если x>x 0, т. е. x - x 0>0, то из (1), т. к. f ¢(c)>0, следует f (x)- f (x 0)>0, т. е. f (x)> f (x 0).
Следовательно, f (x 0) не является ни наименьшим, ни наибольшим значением функции f (x) в  . Значит, x 0 не является точкой экстремума.
. Значит, x 0 не является точкой экстремума. 
Алгоритм нахождения точек экстремума для функции, непрерывной на < a; b >
Пусть f (x) на < a; b > имеет несколько критических точек. Расположим их в порядке возрастания: a < x 1< x 2<…< xn < b. Они делят < a; b > на интервалы (а; x 1), (x 1; x 2),…,(xn; b). В каждом из них f ¢(x 0)¹0, она знакопостоянна (положительна, или отрицательна). Для определения знака производной в интервале надо определить ее знак в любой точке интервала. Затем по изменению знака производной при переходе от одного интервала к другому определим точки экстремума по т 6.
Теорема 7 (второе достаточное условие экстремума). Пусть для функции f в стационарной точке x 0  . Тогда функция имеет в точке x 0 максимум, если
. Тогда функция имеет в точке x 0 максимум, если  и минимум, если
и минимум, если  .
.
Доказательство.
 Пусть
Пусть  . Тогда по теореме 1 f ¢(x) возрастает в точке x 0. Докажем, что x 0 - точка строгого минимума. Т.к. f ¢(x 0)=0, то $ V (x 0, d): f ¢(x)<0 при x<x 0 и f ¢(x)>0 при x > x 0. Тогда по теореме 5 x 0 - точка строгого минимума.
. Тогда по теореме 1 f ¢(x) возрастает в точке x 0. Докажем, что x 0 - точка строгого минимума. Т.к. f ¢(x 0)=0, то $ V (x 0, d): f ¢(x)<0 при x<x 0 и f ¢(x)>0 при x > x 0. Тогда по теореме 5 x 0 - точка строгого минимума.
|
|
|
Для случая  доказательство аналогично.
доказательство аналогично. 
Пример.
D 
f ¢(x)= x 3 - 4 x, f ²(x)=3 x 2 - 4
f ¢(x)=0 при x 1=0, x 2=2, x 3=-2
f ²(0)= - 4 Þ x =0 – точка строго максимума, max f (x)= f (0)=3
f ²(±2)=8 Þ x =±2 – точки строго минимума, min f (x)= f (±2)=-1. D
3. Нахождение наибольшего и наименьшего значений функции на отрезке.
Пусть функция f (x) дифференцируема на отрезке [ a; b ]. Тогда она непрерывна на этом отрезке и, в силу II – й теоремы Вейерштрасса, достигает на нем наибольшего и наименьшего значений. Если функция имеет наибольшее значение на (a; b), то это – один из максимумов. Но функция может иметь наибольшее значение и на концах отрезка [ a; b ]. Аналогичные рассуждения – для минимума. Значит, для нахождения наибольшего и наименьшего значений функции на отрезке [ a; b ] надо:
1) найти все критические точки функции, принадлежащие отрезку [ a; b ];
2) вычислить значения функции в этих точках и на концах отрезка;
3) из полученных значений выбрать наибольшее и наименьшее.
4. Выпуклость функции.
Пусть функция f (x) дифференцируема на < a;b >. Тогда существует касательная к графику функции f (x) в любой точке М (x; f (x)), x Î< a;b >, причем эти касательные не параллельны оси О у.

 Определение. Функция f (x) называется выпуклой вверх (вниз) на < a;b >, если график функции в пределах < a;b > лежит не выше (не ниже) любой из своих касательных.
Определение. Функция f (x) называется выпуклой вверх (вниз) на < a;b >, если график функции в пределах < a;b > лежит не выше (не ниже) любой из своих касательных.
Теорема 8. Пусть функция f (x) дважды дифференцируема на < a;b >. Тогда если f ²(x)³0 (f ²(x)£0) на (a;b), то функция выпукла вниз (вверх) на < a;b >.
Доказательство.
 Пусть f ²(x)³0 " х Î< a;b >. Зафиксируем произвольное х 0Î(a;b). Докажем, что график функции в пределах (a;b) лежит не ниже касательной в точке М 0(x 0; f (x 0)). Уравнение касательной:
Пусть f ²(x)³0 " х Î< a;b >. Зафиксируем произвольное х 0Î(a;b). Докажем, что график функции в пределах (a;b) лежит не ниже касательной в точке М 0(x 0; f (x 0)). Уравнение касательной:
y кас. -f (x 0)= f ¢(x 0)(x-x 0). (1)
Разлагая f (x) по формуле Тейлора для n =1 " х Î(a;b), получим
 , х ¹ х 0, х 0< c < x (x < c < х 0) (2)
, х ¹ х 0, х 0< c < x (x < c < х 0) (2)
Вычтем (1) из (2):
 , с Î(х 0; х) (с Î(х; х 0)). (3)
, с Î(х 0; х) (с Î(х; х 0)). (3)
" х Î(a;b) f ²(x)³0, с Î(х 0; х)Ì(a; b). Следовательно, f ²(с)³0.
Тогда из (3) следует y-y кас.³0 " х Î(a;b), т. е. y ³ y кас. " х Î(a;b). Следовательно, график функции в пределах (a;b) лежит не ниже касательной. Т. к. х 0 - произвольная точка из интервала (a;b), то f (x) выпукла вниз на < a;b >. 
Пример.
D y = f (x)= x 3, 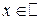
f ¢(x)=3 x 2, f ²(x)=6 x
f ²(x)³0 при x ³0 Þ на [0;+¥) функция выпукла вниз,
f ²(x)£0 при x £0 Þ на (-¥;0] функция выпукла вверх. D
5. Точки перегиба.
Пусть f (x) определена и непрерывна в V (x 0).
Определение. Точка x 0 называется точкой перегиба функции f (x), если при переходе через эту точку меняется направление выпуклости функции f (x).
В примере х =0 – точка перегиба.
Теорема 9 (необходимое условие перегиба). Если в точке перегиба x 0 функции f (x) вторая производная существует и непрерывна, то она в этой точке равна нулю.
|
|
|
Доказательство.
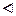 Пусть в точке перегиба x 0 существует непрерывная f ²(x 0). В условиях теоремы для f ²(x 0) возможны 3 случая.
Пусть в точке перегиба x 0 существует непрерывная f ²(x 0). В условиях теоремы для f ²(x 0) возможны 3 случая.
1) f ²(x 0)>0. Следовательно, т. к. f ²(x 0) непрерывна, $ V (x 0), в которой f ²(x)>0, т. е. в точке x 0 функция не меняет направления выпуклости. Значит, x 0 не является точкой перегиба.
2) f ²(x 0)<0. Следовательно, $ V (x 0), в которой f ²(x)<0. Значит, x 0 не является точкой перегиба.
3) f ²(x 0)=0. 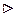
В точке перегиба вторая производная может не существовать.
Пример.
D  ,
, 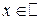 .
.
 ,
,  .
.
Следовательно, в точке х 0=0 f ² не существует.
При x >0 f ²(x)>0 Þ на (0;+¥) функция выпукла вниз,
При x <0 f ²(x)<0 Þ на (-¥;0) функция выпукла вверх.
Значит, х 0=0 - точка перегиба. D
Т. о., точками возможного перегиба являются те точки, в которых вторая производная равна нулю или не существует. Но не каждая такая точка является точкой перегиба.
Пример.
D y = f (x)= x 4 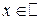
f ¢(x)=4 x 3, f ²(x)=12 x 2.
f ²(x)=0 Û х =0. Но " х f ²(x)³0, следовательно, функция выпукла вниз на  . Значит, х 0=0 не является точкой перегиба, хотя f ²(x 0)=0. D
. Значит, х 0=0 не является точкой перегиба, хотя f ²(x 0)=0. D
Т. о., точки возможного перегиба требуют дальнейшего исследования.
Теорема 10 (первое достаточное условие перегиба). Пусть функция f (x) дважды дифференцируема в  , где x 0 – точка возможного перегиба. Если
, где x 0 – точка возможного перегиба. Если
1) f ²(x) меняет знак при переходе через x 0, то x 0 - точка перегиба функции f (x);
2) f ²(x) не меняет знака при переходе через x 0, то x 0 не является точкой перегиба функции f (x).
Доказательство.
 1) Слева и справа от x 0 функция по теореме 7 имеет разное направление выпуклости, следовательно, x 0 - точка перегиба функции f (x).
1) Слева и справа от x 0 функция по теореме 7 имеет разное направление выпуклости, следовательно, x 0 - точка перегиба функции f (x).
2) В точке x 0 функция не меняет направления выпуклости, следовательно, x 0 не является точкой перегиба. 
Теорема 11. (второе достаточное условие перегиба). Если f ²(x 0)=0, а  , то x 0 - точка перегиба функции f (x).
, то x 0 - точка перегиба функции f (x).
Доказательство.
 По условию
По условию  .
.
Если  , то f ²(x) возрастает в точке x 0. Т. к. f ²(x 0)=0, то
, то f ²(x) возрастает в точке x 0. Т. к. f ²(x 0)=0, то  справа и слева от x 0 имеет разные знаки. Тогда по теореме 9 x 0 - точка перегиба.
справа и слева от x 0 имеет разные знаки. Тогда по теореме 9 x 0 - точка перегиба.
Если  , то f ²(x) убывает в точке x 0. Т. к. f ²(x 0)=0, то
, то f ²(x) убывает в точке x 0. Т. к. f ²(x 0)=0, то  справа и слева от x 0 имеет разные знаки. Следовательно, x 0 - точка перегиба.
справа и слева от x 0 имеет разные знаки. Следовательно, x 0 - точка перегиба. 
Если f ²(x 0)=0 и  , то можно определить перегиб с помощью других достаточных условий, использующих производные высших порядков.
, то можно определить перегиб с помощью других достаточных условий, использующих производные высших порядков.
Асимптоты графика функции
Определение 1. Прямая х = а называется вертикальной асимптотой графика функции f (x), если хотя бы один из односторонних пределов функции в точке а равен +¥ или -¥.
Пример. D х =0 – вертикальная асимптота графика функции 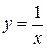 :
:  ,
,  . D
. D
Определение 2. Пусть f (x) определена " x > a (x < a),  . Прямая y = kx + b называется наклонной асимптотой графика функции f (x) при х ®+¥ (х ®-¥), если f (x)= kx + b+a (х), где
. Прямая y = kx + b называется наклонной асимптотой графика функции f (x) при х ®+¥ (х ®-¥), если f (x)= kx + b+a (х), где 
 .
.
При k ¹0 y = kx + b – наклонная асимптота, при k =0 прямая y = b – горизонтальная асимптота.
Теорема. Для того, чтобы прямая y = kx + b являлась наклонной асимптотой графика функции f (x) при х ®+¥ (х ®-¥), необходимо и достаточно, чтобы существовали 2 конечных предела:
 , (1)
, (1)  . (2)
. (2)
Доказательство.
 1) Необходимость.
1) Необходимость.
Пусть прямая y = kx + b – наклонная асимптота графика функции при х ®+¥. Тогда по определению f (x)= kx + b+a (х), где  . Отсюда
. Отсюда
 ,
,
 .
.
2) Достаточность.
Пусть существуют пределы (1) и (2). Из (2) следует f (x) -kx = b+a (х), где  . Следовательно, f (x)= kx + b+a (х), и, значит, прямая y = kx + b является наклонной асимптотой графика функции f (x) при х ®+¥.
. Следовательно, f (x)= kx + b+a (х), и, значит, прямая y = kx + b является наклонной асимптотой графика функции f (x) при х ®+¥. 
Пример. Найти асимптоты графика функции  .
.
D 1) Вертикальные асимптоты.
 .
.
Функция является элементарной, следовательно, непрерывна в области определения, х =0 – точка разрыва. Найдем односторонние пределы в этой точке:
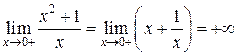 ,
,  .
.
Следовательно, х =0 – точка разрыва второго рода, прямая х =0 – вертикальная асимптота графика функции.
2) Наклонные асимптоты.
1 способ (по определению).  . Т. е. f (x)= kx + b+a (х), где k =1, b =0,
. Т. е. f (x)= kx + b+a (х), где k =1, b =0,  . Значит, прямая y = x – наклонная асимптота графика функции при х ®±¥.
. Значит, прямая y = x – наклонная асимптота графика функции при х ®±¥.
 2 способ (по теореме).
2 способ (по теореме).
 Þ k =1,
Þ k =1,
 Þ b =0. Следовательно, прямая y = x – наклонная асимптота графика функции при х ®±¥. D
Þ b =0. Следовательно, прямая y = x – наклонная асимптота графика функции при х ®±¥. D
Схема полного исследования функции.
1. Найти область определения (и множество значений, если просто).
2. Исследовать функцию на четность, нечетность, периодичность.
3. Исследовать функцию на непрерывность, найти точки разрыва и вертикальные асимптоты (если есть).
4. Исследовать поведение функции в окрестности граничных точек области определения и при х ®±¥.
5. Найти (если есть) наклонные асимптоты графика функции.
6. Исследовать функцию на монотонность и экстремум.
7. Исследовать функцию на направление выпуклости и точки перегиба.
8. Найти точки пересечения графика функции с осями координат и промежутки знакопостоянства.
9. Построить график.
Пример.  .
.
1)  .
.
2) Функция не является ни четной, ни нечетной, не является периодической.
3) х =-3 – точка разрыва.
 ,
,  .
.
Следовательно, х =-3 – точка разрыва второго рода, прямая х =-3 – вертикальная асимптота графика функции.
4)  ,
,  .
.
5)  ,
,  .
.
При х ®-¥ k =0.
 .
.
b =0 при х ®-¥. Следовательно, прямая у=0 – горизонтальная асимптота графика функции при х ®-¥.
При х ®+¥ наклонных асимптот нет.
 6)
6)  .
.

х =-2 – точка минимума, у (-2)= е – минимум.
7) 


 на D (f), y ² не существует в точке х =-3.
на D (f), y ² не существует в точке х =-3.
Точек перегиба нет.
8) Ось О х график не пересекает.
Ось О у: х =0,  .
.
 y >0 при x Î(-3;+¥), y <0 при x Î(-¥;0).
y >0 при x Î(-3;+¥), y <0 при x Î(-¥;0).
|
|
|


