 |
Потенциал. Потенциальная энергия заряда в поле.
|
|
|
|
Закон Кулона. Принцип суперпозиции полей.
Закон Кулона. Из опыта непосредственно следует, что напряженность поля неподвижного точечного заряда q на расстоянии 
от него можно представить как
(*)
где 
— электрическая постоянная; 
— орт радиуса-вектора 
, проведенного из центра поля, в котором расположен заряд q, до интересующей нас точки. Формула (*) записана в СИ. Здесь коэффициент
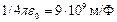
заряд q определяют в кулонах (Кл), напряженность поля 
— в вольтах на метр (В/м). В зависимости от знака заряда q вектор направлен так же, как и , или противоположно ему. По существу формула (*) выражает не что иное, как закон Кулона, но в «полевой» форме. Весьма важно, что напряженность поля точечного заряда обратно пропорциональна квадрату расстояния 
. Вся совокупность экспериментальных фактов показывает, что этот закон справедлив для расстояний от 
см до нескольких километров, и пока нет никаких оснований ожидать, что этот закон не выполняется и при больших расстояниях.
Заметим еще, что в поле, создаваемом неподвижным точечным зарядом, сила, действующая на пробный заряд, не зависит от того, покоится пробный заряд или движется. Это относится и к системе неподвижных зарядов.
Принцип суперпозиции. Н апряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:
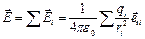
где 
— расстояние между зарядом 
и интересующей нас точкой поля.
Это утверждение называют принципом суперпозиции (наложения) электрических полей. Он выражает одно из самых замечательных свойств полей и позволяет вычислять напряженность поля любой системы зарядов, представив ее в виде совокупности точечных зарядов, вклад каждого из которых дается формулой (*).
|
|
|
Потенциал. Потенциальная энергия заряда в поле.
Потенциал. До сих пор мы рассматривали описание электрического поля с помощью вектора . Существует, однако, и другой адекватный способ описания — с помощью потенциала 
(заметим сразу, что оба эти способа однозначно соответствуют друг другу). Как мы увидим, второй способ обладает рядом существенных преимуществ.
Тот факт, что линейный интеграл 
, представляющий собой работу сил поля при перемещении единичного положительного заряда из точки 1 в точку 2, не зависит от пути между этими точками, позволяет утверждать, что в электрическом поле существует некоторая скалярная функция координат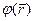 
, убыль которой
(1)
где 
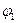и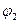 
— значения функции в точках 1 и 2. Так определенная величина 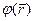называется потенциалом поля. Из сопоставления выражения (1) с выражением для работы сил потенциального поля (которая равна убыли потенциальной энергии частицы в поле) можно сказать, что потенциал — это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля.
Потенциалу какой-либо произвольной точки О поля можно условно приписать любое значение 
. Тогда потенциалы всех других точек поля определяются согласно (1) однозначно. Если изменить ф0 на некоторую величину 
, то на такую же величину изменятся и потенциалы во всех других точках поля.
Таким образом, потенциал определяется с точностью до произвольной аддитивной постоянной. Значение этой постоянной не играет роли, так как все электрические явления зависят только от напряженности электрического поля. Последняя же определяется, как мы увидим, не самим потенциалом в данной точке поля, а разностью потенциалов в соседних точках поля.
Единицей потенциала является вольт (В).
Потенциальная энергия заряда в поле. Формула (1) содержит не только определение потенциала , но и способ нахождения этой функции. Для этого достаточно вычислить интеграл 
по любому пути между двумя точками и представить затем полученный результат в виде убыли некоторой функции, которая и есть 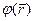. Можно поступить и проще. Воспользуемся тем, что формула (1) справедлива не только для конечных перемещений, но и для элементарных 
. Тогда согласно этой формуле элементарная убыль потенциала на этом перемещении есть
|
|
|
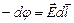
Другими словами, если известно поле 
, то для нахождения надо представить 
(путем соответствующих преобразований) как убыль некоторой функции. Эта функция и есть .
Найдем таким способом потенциал поля неподвижного точечного заряда:
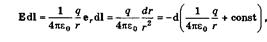
где учтено, что 
, ибо проекция вектора на вектор , а значит, и на равна приращению модуля вектора , т. е. 
. Величина, стоящая в круглых скобках под знаком дифференциала, и есть 
. Так как присутствующая здесь аддитивная константа никакой физической роли не играет, ее обычно опускают, стремясь выражение для сделать проще. Таким образом, потенциал поля точечного заряда
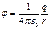
Отсутствие в этом выражении аддитивной константы означает, что мы условно полагаем потенциал на бесконечности 
равным нулю.
|
|
|
