Мкость проводников и конденсаторов

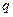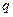Электроемкость уединенного проводника. Рассмотрим какой-либо уединенный проводник, т.е. проводник, удаленный от других проводников, тел и зарядов. Опыт показывает, что между зарядом такого проводника и его потенциалом (потенциал на бесконечности мы условились считать равным нулю) существует прямая пропорциональность: . Следовательно, не зависит от заряда , для каждого уединенного проводника это отношение имеет свое значение. Величину 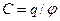называют электроемкостью уединенного проводника (сокращенно емкостью). Емкость зависит от размеров и формы проводника. Единицу емкости называют фарадам. (Ф).

Конденсаторы. Если проводник не уединен, то его емкость будет существенно увеличиваться при приближении к нему других тел. Это обусловлено тем, что поле данного проводника вызывает перераспределение зарядов на окружающих телах — появление индуцированных зарядов. Пусть заряд проводника 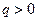. Тогда отрицательные индуцированные заряды оказываются ближе к проводнику, нежели положительные. Поэтому потенциал проводника, являющийся алгебраической суммой потенциала собственных зарядов и зарядов, индуцированных на других телах, уменьшится при приближении к нему других незаряженных тел. А значит, его емкость увеличится. Это позволило создать систему проводников (конденсатором), которая обладает емкостью, значительно большей, чем уединенный проводник, и притом не зависящей от окружающих тел. Простейший конденсатор состоит из двух проводников (обкладок), расположенных на малом расстоянии друг от друга.

Чтобы внешние тела не оказывали влияния на емкость конденсатора, его обкладки располагают так относительно друг друга, чтобы поле, создаваемое накапливающимися на них зарядами, было сосредоточено практически полностью внутри конденсатора. Это означает, что линии вектора Е, начинающиеся на одной обкладке, должны заканчиваться на другой, т. е. заряды на обкладках должны быть одинаковы по модулю и противоположны по знаку (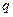 и ).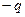

Основной характеристикой конденсатора является его емкость. В отличие от емкости уединенного проводника под емкостью конденсатора понимают отношение заряда конденсатора к разности потенциалов между обкладками (эту разность называют напряжением): . Под зарядом 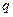конденсатора имеют в виду заряд, расположенный на положительно заряженной обкладке. Естественно, емкость конденсатора измеряют также в фарадах. Емкость конденсатора зависит от его геометрии (размеров и формы обкладок), от зазора между ними и от заполняющей конденсатор среды.

Емкость плоского конденсатора. Этот конденсатор состоит из двух параллельных пластин, разделенных зазором шириной . Если заряд конденсатора 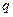, то напряженность поля между его обкладками 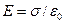, где 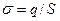, — площадь каждой пластины. Следовательно, напряжение между обкладками 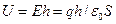. Подстановляя этого выражения в получим

Этот расчет был проведен без учета искажения поля у краев пластин (без учета краевых эффектов). Емкость реального плоского конденсатора определяется полученным выражением тем точнее, чем меньше зазор по сравнению с линейными размерами пластин.

Емкость сферического конденсатора. Пусть радиусы внутренней и внешней обкладок конденсатора равны соответствен­но а и b. Если заряд конденсатора q, то напряженность поля между обкладками определяется по теореме Гаусса: 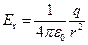, Напряжение на конденсаторе 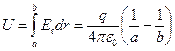, Отсюда легко видеть, что емкость сферического конденсатора 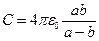. Полезно убедиться, что в случае малого зазора между об­кладками, т. е. при условии 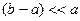(или b), полученное вы­ражение переходит в — в выражение для емкости плос­кого конденсатора.

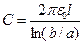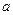Емкость цилиндрического конденсатора. Рассуждая так же, как и в случае со сферическим конденсатором, получим , где — длина конденсатора; и 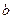— радиусы внутренней и на­ружной цилиндрических обкладок. Здесь так же, как и в пре­дыдущем случае, при малом зазоре между обкладками полу­ченное выражение переходит в .