 |
Закон Ома для участка цепи.
|
|
|
|
Закон Ома для однородного участка цепи. Закон Ома, открытый экспериментально, гласит: сила тока, протекающего по однородному проводнику, пропорциональна разности потенциалов на его концах (напряжению U):
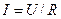
где R — электрическое сопротивление проводника.
Единицей сопротивления служит ом (Ом).
Сопротивление R зависит от формы и размеров проводника, от его материала и температуры, а также — это следует помнить — от конфигурации (распределения) тока по проводнику. В случае провода смысл сопротивления не вызывает сомнений. В более общем случае объемного распределения тока уже нельзя говорить о сопротивлении, пока не указаны или расположение подводящих к интересующему нас проводнику проводов, или конфигурация тока.
В простейшем случае однородного цилиндрического проводника сопротивление
(1)
где 
— длина проводника; 
— площадь его поперечного сечения; 
— удельное электрическое сопротивление. Последнее зависит от материала проводника и его температуры. Выражают в ом-метрах (Ом∙м).
Значения удельного электрического сопротивления для наиболее хороших проводников (медь, алюминий) составляют при комнатной температуре несколько единиц на 
Ом∙м.
Закон Ома в локальной форме. Найдем связь между плотностью тока 
и полем 
в одной и той же точке проводящей среды. Ограничимся случаем изотропного проводника, в котором направления векторов и совпадают.
Выделим мысленно в окрестности некоторой точки проводящей среды элементарный цилиндрический объем с образующими, параллельными вектору , а значит, и вектору . Если поперечное сечение цилиндра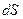 
, а его длина 
, то на основании (5.8) и (5.9) можно записать для такого элементарного цилиндра
|
|
|
и после соответствующих сокращений получим, уже в векторном виде,
где 
— удельная электропроводимость среды. Единицу, обратную ому, называют сименсом (См), поэтому единицей ст является сименс на метр (См/м).
Закон Ома для неоднородного участка цепи. Неоднородным называют участок цепи, на котором действуют сторонние силы.
Рассмотрим частный, но практически важный случай, когда электрический ток течет вдоль тонких проводов. В этом случае направление тока будет совпадать с направлением оси провода и плотность тока 
может считаться одинаковой во всех точках сечения провода. Пусть площадь сечения провода равна S, причем S может быть и не одинаковой по длине провода.
Разделим уравнение 
на 
, полученное выражение умножим скалярно на элемент оси провода 
, взятый по направлению от сечения 1 к сечению 2 (его мы примем за положительное), и затем проинтегрируем по длине провода от сечения 1 до сечения 2:
(3)
Преобразуем подынтегральное выражение у первого интеграла: заменим на 
и 
на 
, где 
— проекция вектора на направление вектора . Далее учтем, что — величина алгебраическая; она зависит от того, как направлен вектор по отношению к : если 
, то 
, если же 
, то 
. И последнее, заменим на 
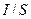, где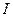 
— сила тока, величина тоже алгебраическая (как и ). Поскольку для постоянного тока 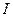одинаково во всех сечениях цепи, эту величину можно вынести за знак интеграла. В результате получим
Выражение 
определяет не что иное, как сопротивление участка цепи длиной , а интеграл от этого выражения — полное сопротивление R участка цепи между сечениями 1 и 2.
Теперь обратимся к правой части (3). Первый интеграл здесь — это разность потенциалов 
, а второй интеграл представляет собой электродвижущую силу (э.д.с.) 
, действующую на данном участке цепи:
Эта величина, как и сила тока 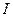, является алгебраической: если э.д.с. способствует движению положительных носителей тока в выбранном направлении, то 
, если же препятствует, то 
.
|
|
|
После всех указанных преобразований уравнение (3) будет иметь следующий вид:
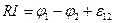
где положительным считается направление от точки 1 к точке 2.
Удельная мощность тока.
Отношение мощности 
, развиваемой током в объеме проводника 
, к этому объему называется удельной мощностью тока 
, отвечающей данной точке проводника. По определению удельная мощность равна
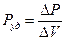
Условно говоря, удельная мощность есть мощность, развиваемая в единице объема проводника.
Выражение для удельной мощности тока можно получить, исходя из следующих соображений. Сила 
развивает при движении носителя тока мощность, равную
Усредним это выражение по носителям, заключенным в объеме , в пределах которого и 
можно считать постоянными. В результате получим
(напомним, что 
).
Мощность , развиваемую в объеме , можно найти, умножив 
на число носителей тока в этом объеме, которое равно 
(
— число носителей в единице объема). Таким образом,
Отсюда
|
|
|
