 |
Условия на границе двух магнетиков.
|
|
|
|
Речь идет об условиях для векторов 
и 
на границе раздела двух однородных магнетиков. Эти условия, как и в случае диэлектрика, мы получим с помощью теоремы Гаусса и теоремы о циркуляции. Для векторов и эти теоремы, напомним, имеют вид
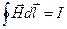
Условие для вектора . Представим себе очень малой высоты цилиндрик, расположенный на границе раздела магнетиков, как показано на рисунке. Тогда поток вектора наружу из этого цилиндрика (потоком через боковую поверхность пренебрегаем) можно записать так:
Взяв обе проекции вектора на общую нормаль 
, получим 
,и предыдущее уравнение после сокращения на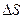 
примет следующий вид:
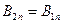
т. е. нормальная составляющая вектора оказывается одинаковой по обе стороны границы раздела. Эта величина скачка не испытывает.
Условия для вектора . Для большей общности будем предполагать, что вдоль поверхности раздела магнетиков течет поверхностный ток проводимости с линейной плотностью 
. Применим теорему о циркуляции вектора к очень малому прямоугольному контуру, высота которого пренебрежимо мала по сравнению с его длиной 
, расположив этот контур так, как показано на рисунке. Пренебрегая вкладом в циркуляцию на боковых сторонах контура, запишем для всего кон тура:
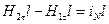
где 
— проекция вектора на нормаль 
к контуру (вектор образует с направлением обхода по контуру правовинтовую систему). Взяв обе проекции вектора на общий орт касательной 
(в среде 2), получим 
, и после сокращения на предыдущее уравнение примет вид
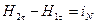
т. е. тангенциальная составляющая вектора , вообще говоря, при переходе границы раздела магнетиков претерпевает скачок, связанный с наличием поверхностных токов проводимости.
|
|
|
Однако если на границе раздела магнетиков токов проводимости нет (
), то тангенциальная составляющая вектора оказывается одинаковой по обе стороны границы раздела:
Итак, если на границе раздела двух однородных магнетиков тока проводимости нет, то при переходе этой границы составляющие 
и 
изменяются непрерывно, без скачка. Составляющие же 
и 
при этом претерпевают скачок.
33. Связь магнитного и механического моментов.
Найдем магнитный момент:
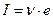
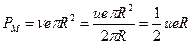
Найдем механический момент:
(знак минус из-за того моменты направлены в разные стороны)
Следовательно:
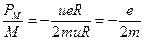
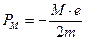
ЭДС индукции.
Открытие Фарадея. В 1831 г. Фарадеем было сделано одно из наиболее фундаментальных открытий в электродинамике — явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении магнитного потока (т. е. потока вектора В), охватываемого этим контуром, возникает электрический ток — его назвали индукционным.
Закон электромагнитной индукции. Согласно этому закону, какова бы ни была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с. индукции" определяется формулой
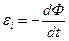
Знак минус в этом уравнении связан с определенным правилом знаков. Знак магнитного потока Ф связан с выбором нормали к поверхности S, ограниченной рассматриваемым контуром, а знак э.д.с. индукции 
— с выбором положительного направления обхода по контуру.
Здесь предполагается (как и ранее), что направление нормали к поверхности S и положительное направление обхода контура связаны друг с другом правилом правого винта (рисунок). Поэтому, выбирая (произвольно) направление нормали, мы определяем как знак потока Ф, так и знак (а значит, и «направление») э.д.с. индукции
При сделанном нами выборе положительных направлений — в соответствии с правилом правого винта — величины и 
имеют противоположные знаки.
|
|
|
Единицей магнитного потока является вебер (Вб). При скорости изменения магнитного потока 1 Вб/с в контуре индуцируется э.д.с., равная 1 В.
|
|
|
