 |
Основные уравнения магнитостатики.
|
|
|
|
Теорема Гаусса для поля 
. Поток вектора сквозь любую замкнутую поверхность равен нулю:
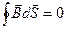
Эта теорема является, по существу, обобщением опыта. Она выражает собой в постулативной форме тот экспериментальный факт, что линии вектора не имеют ни начала, ни конца.
Поэтому число линий вектора , выходящих из любого объема, ограниченного замкнутой поверхностью S, всегда равно числу линий, входящих в этот объем.
Отсюда вытекает важное следствие, которым мы будем пользоваться в дальнейшем неоднократно. А именно: поток вектора сквозь поверхность S, ограниченную некоторым замкнутым контуром, не зависит от формы поверхности S. Это легко понять с помощью представления о линиях вектора : так как они нигде не прерываются, их число сквозь поверхность S, ограниченную данным контуром (т. е. поток вектора ), действительно не должно зависеть от формы поверхности S.
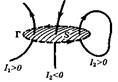
Теорема о циркуляции вектора (для магнитного поля постоянных токов в вакууме). Циркуляция вектора по произвольному контуру Г равна произведению 
на алгебраическую сумму токов, охватываемых контуром Г:
(1)
где 
, причем 
— величины алгебраические. Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта. Ток противоположного направления считается отрицательным. Это правило иллюстрирует рисунке: здесь токи 
и 
положительные, ибо их направления связаны с направлением обхода по контуру правилом правого винта, а ток 
— отрицательный.
Закон Ампера.
Закон Ампера. Каждый носитель тока испытывает действие магнитной силы. Действие этой силы передается проводнику, по которому заряды движутся. В результате магнитное поле действует с определенной силой на сам проводник с током. Найдем эту силу.
|
|
|
Пусть объемная плотность заряда, являющегося носителем тока (электроны в металле, например), равна 
. Выделим мысленно элемент объема 
проводника. В нем находится заряд — носитель тока, равный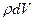 
. Тогда сила, действующая на элемент проводника, может быть записана по формуле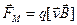 
в виде
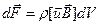
где 
— скорость упорядоченного движения зарядов.
Так как 
, то
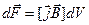(1)
Если ток течет по тонкому проводнику, то согласно 
(6.8) и
(2)
где 
— вектор, совпадающий по направлению с током и характеризующий элемент длины тонкого проводника.
Формулы (1) и (2) выражают закон Ампера.
Сила Лоренца.
Сила Лоренца. Опыт показывает, что сила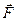 
, действующая на точечный заряд 
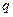, зависит в общем случае не только от положения этого заряда, но и от его скорости 
. Соответственно этому силу 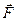разделяют на две составляющие — электрическую 
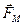(она не зависит от движения заряда) и магнитную 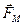(она зависит от скорости заряда). В любой точке пространства направление и модуль магнитной силы зависят от скорости заряда, причем эта сила всегда перпендикулярна вектору ; кроме того, в любом месте магнитная сила перпендикулярна определенному в данном месте направлению и, наконец, ее модуль пропорционален той составляющей скорости, которая перпендикулярна этому выделенному направлению.
Все эти свойства магнитной силы можно описать, если ввести понятие магнитного поля. Характеризуя это поле вектором , определяющим выделенное в каждой точке пространства направление, запишем выражение для магнитной силы в виде
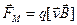
Тогда полная электромагнитная сила, действующая на заряд :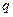
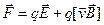
Ее называют силой Лоренца. Последнее выражение является универсальным: оно справедливо как для постоянных, так и для переменных электрических и магнитных полей, причем при любых значениях скорости заряда. Заметим, что — это скорость заряда относительно интересующей нас системы отсчета.
|
|
|
|
|
|
