 |
Сформулировать арифметические теоремы о пределах (предел суммы, произведения и частного двух функций).
|
|
|
|
Сформулировать арифметические теоремы о пределах (предел суммы, произведения и частного двух функций).
Это про свойства пределов, сложение умножение и т. д.
Определение бесконечно большой функции при данном стремлении аргумента. Доказать теорему о связи бесконечно большой и бесконечно малой функций.
f(x) называется бесконечно большой если
∀ e> 0 ∃ d(e)> 0): (x∈ ВыклОкрd(*))=> |f(x)|> e
Если функция f(x) бесконечно большая при x → a, то функция
1/f(x) является бесконечно малой при x → a. Док-во. limx→ a f(x) = ∞ ⇒ ∀ ε > 0 ∃ ВыклОкрU(a) ∀ x∈ ВыклОкрU(a): |f(x)| > 1/ε. |f(x)| > 1/ε ⇒ 1/|f(x)| < ε ⇒ limx→ a 1/f(x) = 0 ⇒ 1/f(x) - бесконечно малая при x → a.
Доказать теорему о «первом замечательном пределе». Сформулировать ее следствия. Доказать два из них.
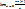=1
Док-во.
Рассмотрим 
и 
Докажем что они = 1. Пусть x∈ (0; 
) отложим его на ед окр.
Пусть K — точка пересечения второй стороны угла с единичной окружностью, а точка L — с касательной к этой окружности в точке A (1; 0). Точка H — проекция точки K на ось OX.
S∆ OKA < S∆ sectKOA < S∆ OAL
|KH|=sin(x), |LA|= tg(x) => S∆ OKA= 
∙ |OA|∙ |KH|= ∙ 1∙ sin x = 
; S∆ sectKOA= ∙ |OA|2∙ x= 
; S∆ OAL= ∙ |OA|∙ |LA|= 
< < ; 
< 
< 
; cos x < 
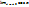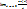< 1
≤ 
≤ 1; 
Функция чётная - Тр. доказана
Следствия:
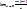=1; замена y=ax
=1 разложить тангенс
=1; замена y=arcsin(x) x= 
=1 аналог предыд
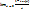=1; 1- cos x 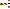= 2 ( 
)2
Сформулировать теорему о «втором замечательном пределе» и ее следствия. Доказать два из них.
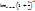=e
Следствия:
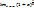=e замена y=
=1 внести степень
=1 замена y=ex-1
=ea замена y= 
Сравнение функций при данном стремлении аргумента, определение отношений «~» «о-малое» и «О-большое», примеры. Сформулировать теоремы об эквивалентных функциях (свойства отношения эквивалентности). Определение порядка малости (или роста) одной функции относительно другой при данном стремлении аргумента. Привести примеры.
|
|
|
Пусть f(x) и g(x) — две функции, определенные в некоторой проколотой окрестности точки x0, причем в этой окрестности g не обращается в ноль.
f является «O» большим от g при x®x0, если существует такая константа C> 0, что для всех x из некоторой окрестности точки x0имеет место неравенство
|f(x)|≤ C|g(x)|;
f является «о» малым от g при x®x0, если для любого ε > 0 найдется такая проколотая окрестность U’x0 точки x0, что для всех x∈ U’x0 имеет место неравенство
|f(x)|≤ ε |g(x)|;
Если f(x)~g(x) и g(x)~h(x), то f(x)~h(X)
Определение непрерывности функции в точке. Односторонняя непрерывность в точке, ее связь с (обычной) непрерывностью в точке. Доказать теорему о переходе к пределу под знаком непрерывной функции. Доказать теорему о непрерывности композиции двух непрерывных функций.
Для того чтобы F(x) была непрерывна в точке x0, необходимо и достаточно, чтобы она была непрерывна в этой точке, как слева, так и справа.
Если две функции непрерывны то и их сумма/произведение непрерывна/о.
Сформулировать теорему о непрерывности основных элементарных функций и теорему о непрерывности элементарных функций. Сформулировать локальные свойства функции, непрерывной в точке х0: локальная ограниченность, локальное знакопостоянство (если f(x0)≠ 0).
Основные элементарные функции непрерывны в области определения.
Функция, непрерывна в точке x0, локально ограничена в этой точке.
Если функция непрерывна в точке x0 и f(x0) ≠ 0, то существует окрестность точки x0 в которой знак функции совпадает с ее знаком в точке x0.
Определение функции, непрерывной на интервале, полуинтервале, отрезке. Сформулировать теоремы о свойствах функции, непрерывной на отрезке. Привести примеры, иллюстрирующие существенность условий в формулировках этих теорем. Сформулировать теорему о непрерывности функции, обратной к монотонной и непрерывной функции.
|
|
|
Функция определённая на интервале называется непрерывной, если она непрерывна в каждой его точке.
Дополнительно условие зависит от [] скобок, там где такая скобка функция должна быть непрерывна в конкретной точке с указанием стороны непрерывности по стремлению со стороны.
Если функция y=f(x) непрерывна и строго возрастает на отрезке [a, b], то на отрезке [f(a), f(b)] определена функция x=g(y) обратная к f, непрерывная и строго возрастающая.
|
|
|
