 |
Сформулировать правило Лопиталя-Бернулли и доказать его для случая неопределенности. Раскрытие неопределенностей других видов.
|
|
|
|
Сформулировать правило Лопиталя-Бернулли и доказать его для случая неопределенности. Раскрытие неопределенностей других видов.
Теорема. Пусть в некоторой окрестности u(a) точки α определены функции f (x) и ф(x), удовлетворяющие следующими условиям:
1. f(x) и ф(x) дифференцируемы в u(a)
2. f(a) = 0 и ф(a)=0; или стремятся к бесконечности при x -> a
3. ф'(x) ≠ 0, в u(a)
4. ∃  = A
= A
Тогда существует  = A
= A
Доказательство. Пусть x ∈ u(a). Тогда, при x> a, на отрезке [a, x] a x (при x < a, на отрезке [x, a]) функции f и ф удовлетворяют условиям теоремы Коши.
Следовательно, ∃ c ∈ (a, x) (либо, соответственно, интервалу (x, a)) такая, что

или, с учетом того, что f(a)=0 и ф(a)=0,
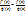
Переходя к пределу при x -> a, с учетом того, что отрезок [a, x] ([x, a]), внутри которого находится точка c в этом пределе стягивается в точку, т. е. c -> x, получим:

Определение многочлена Тейлора в данной точке. Сформулировать теорему о равенстве значений и в этой точке функции и её многочлена Тейлора, а также их производных.
Пусть функция у= f(х), определенная в некоторой окрестности точки х0, дифференцируема в этой точке. Тогда, как известно, приращение данной функции в точке х0, представимо в виде:
∆ у= f(х)- f(х0) = f'(х0) ∆ х +o(∆ х), где ∆ х=х-х0
Иными словами,
F(х) = f(x0) + f’(x0)(х-х0)+o(х-х0) при x®x0
Это равенство представляет собой формулу Тейлора 1-го порядка. В общем случае, формула Тейлора позволяет приближать функцию f(х) многочленом n-ой степени, причем, выбирая достаточно большое n, можно получить
сколь угодно высокую точность приближения.
Сформулировать теоремы о представимости функции по формуле Тейлора с остаточным членом: (а) в форме Пеано, (б) в форме Лагранжа. Формула Маклорена, как частный случай формулы Тейлора.
|
|
|
Пусть f имеет n производных в точке x0 и Tn — многочлен Тейлора для функции f в окрестности точки x0. Тогда
f(x)=Tn(x)+o((x− x0)n), x→ x0.
Пусть функция f определена в окрестности точки a. Пусть точка b принадлежит этой окрестности и для определенности b> a. Предположим также, что функция f имеет (n+1) производную на интервале (a, b) и n производных на отрезке [a, b], причём f(n) непрерывна на [a, b]. Обозначим через Tn тейлоровский многочлен функции f в окрестности точки a. Тогда найдётся такая точка c∈ (a, b), что
f(b)=Tn(b) + 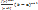
Доказать достаточное условие и сформулировать необходимое условие монотонности дифференцируемой функции. Доказать достаточные признаки экстремума функции: первый (в критической точке – по первой производной), второй (в стационарной точке – по второй производной).
Для того чтобы дифференцируемая функция f(x) на интервале (a, b) была возрастающая, необходимо и достаточно, чтобы ∀ x∈ (a; b) f’(x) ≥ 0.
Определение выпуклости функции (её графика) на промежутке. Доказать достаточное условие выпуклости графика.
Определение точки перегиба графика. Доказать необходимое условие перегиба графика в данной точке. Доказать достаточное условие перегиба графика в точке.
Точкой перегиба называется точка, в которой график меняет свою выпуклость.
Предположим, что f''(x0) ≠ 0. Тогда f''(x0> 0 либо f''(x0)< 0.
По условию f'' непрерывна в точке x0, по свойству сохранения знака непрерывной функции получим: ∃ d: ∀ x∈ Ud(x0), f''(x)=f''(x0), т. е по достаточному условию строгой выпуклости f''(x)> 0 ∀ x∈ (a; b) (функция выпукла вниз) или f''(x)< 0 ∀ x∈ (a; b) (функция выпукла вверх). Это противоречит определению точки перегиба, которое гласит, что при переходе через точку x0 направление выпуклости меняется.
Пусть f'' меняет знак с «-» на «+», тогда по достаточному условию строгой выпуклост функция f(x) на интервале (x0-d; x) функция будет строго выпукла вверх, на интервале (x0; x0+d ) — строго выпукла вниз, т. е при переходе через точку x0 направление выпуклости изменяется => по определению x0— точка перегиба.
|
|
|
При переходе через точку x=1 функция изменяет направление выпуклости, значит x=1 — точка перегиба графика функции.
Схема полного исследования функции и построения (эскиза) ее графика.
1) Область определения и точки разрыва
2)Четность нечётность, периодичность
3) Точки пересечения с осями координат
4) Интервалы знакопостоянства
5) Асимптоты
6) Монотонности и точки экстремума
7) Интервалы выпуклости
|
|
|


