 |
Определение точки разрыва функции. Классификация точек разрыва. Примеры.
|
|
|
|
Определение точки разрыва функции. Классификация точек разрыва. Примеры.
Точки, в которых нарушается условие непрерывности, называют точками разрыва функции.
Точка разрыва х0 называется точкой разрыва первого рода, если существуют конечные односторонние пределы в этой точке.
Точка разрыва первого рода называется точкой устранимого разрыва, если односторонние пределы в этой точке равны.
Точка х0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или равен ±¥.
Определение асимптоты графика функции. Критерий существования горизонтальной и вертикальной асимптот. Вывести формулы для вычисления коэффициентов.
Асимптотой графика функции называется прямая такая, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
d = f(x)-kx-b; d→ 0; k = 
k 
; b= 
Определение производной функции в точке, ее геометрический, механический и экономический смысл. Определение касательной и нормали к графику функции. Уравнения касательной и нормали.
f’(x)=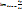 
= 
y-y0=f’(x0) · (x-x0)
y-y0= -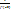 
∙ (x-x0)
Определение дифференцируемости функции в точке. Сформулировать теорему о связи дифференцируемости и существовании конечной производной.
Функция y = f(x) называется дифференцируемой в точке x0, если ее приращение ∆ f в этой точке можно представить в виде: ∆ f=A·∆ x+◦ (∆ x), ∆ x→ 0,
где A - постоянная, ∆ x = x − x0, ∆ f = f(x) − f(x0).
Если функция имеет дифференциал в некоторой точке, то она имеет производную в этой точке и наоборот.
Односторонние производные. Связь односторонних производных с обычной (двусторонней).
|
|
|
Односторонней производной функции в точке называется предел отношения приращения функции в этой точке к соответствующему приращению аргумента, при стремлении последнего к нулю со стороны производной.
Функция имеет в точке конечную производную тогда и только когда она имеет в ней обе конечных односторонних производных.
Сформулировать правила дифференцирования суммы, произведения и частного двух функций. Доказать два из них. Сформулировать теоремы о производной: сложной и обратной функций. Вывести формулы для производных константы, показательной, логарифмической, степенной и тригонометрической функций.
Просто написать, как находить производные по формуле.
Определение эластичности одной экономической величины по отношению к другой, связь с производной, преимущества эластичности перед производной.
Эластичность — мера чувствительности одной переменной (например, спроса или предложения) к изменению другой (например, цены, дохода), показывающая на сколько процентов изменится первый показатель при изменении второго на 1%. Преимущество: показывает степень взаимосвязи.
Логарифмическое дифференцирование. Нахождение производной функций вида (u(x)) v(x). Дифференцирование произведений и дробей с большим числом сомножителей в числителе и знаменателе.
Суть такого дифференцирования заключается в следующем: вначале находится логарифм заданной функции, а уже затем вычисляется от него производная. Помогает при поиске производны от сложных функций.
(u(x) v(x))’ = (ev(x)*ln(u(x)))’ и т. д.
Физический смысл второй производной. Дифференцирование функции, заданной неявно. Нахождение первой и второй производных функции, заданной параметрически.
Производная неявной функции:
На первом этапе навешиваем штрихи на обе части
Используем правила линейности производной
|
|
|
Непосредственное дифференцирование.
Важно понимать, что в неявно заданной функции y является функцией поэтому например:
(sin y)’ = y’ * cos y
Производная параметрической функции:
y’x=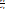 
; y’’xx=(y’x)’x = 
|
|
|
